
「この院生はノーベル賞を授かる」とアインシュタインが評した論文(1924年)その7
その6からの続きです。いよいよ1924年に突入です。
この1924年に、ルイくんはアルちゃんより「こいつ博士号よりノーベル賞に値する」と称えられるわけですが、その博士論文の読解に入る前に、もうひとつ別のものを読解しておきましょう。
英語です。今まで見てきたものはフランス語でしたが今度のは英語論文です。えげれその科学雑誌の老舗「Philosophical Magazine」向けに英語で書かれたものです。
「光量子の試論」("A tentative theory of light quanta")というタイトルです。

全13ページ。内容は、前年ルイくんがフランス語で書き記した三論文を、ひとつに整理したものです。
英語で書かれているので、なんとか読めるという方は読めると思います。
*
冒頭段落を見てみると、重要キーワードでいっぱいです。「光量子」「輻射と物質とのエネルギー交換」「光電効果」「アインシュタインの光電原理」「散乱Ⅹ線」「波長」「コンプトン」「ボーア」「hν」「黒体放射」「放出と吸収」など。
ルイくんの語りは、前年のものよりずっとなめらかです。考えが整理されてきているのがわかります。全訳してそのまま紹介しても伝わるくらいですが、ここでは私の要約でちゃちゃっと紹介していきます。
「アインシュタインによって提示された『光量子』の考え方を使わずしては説明のつかないことが今やいくつかの実験によってはっきりしている」うんぬん。ここまではどなたもうなずく内容です。
ここからだんだんルイくん独自の理論に入っていくのです。「『光量子』は観念的なものではなく実在する粒子と考えて以下計算していきます」と。
ルイくんのいう「実在する」とは、質量がわずかとはいえ存在するということです。
もちろん今の私たちにすれば「なんで光に質量あるねん?」とツッコみたくなるのですが、彼が当時目指したのはアインシュタインの「光量子」すなわちデジタルな物理イメージを、旧来の「波動」つまりアナログ的思考と、どう融合させるか、でした。
そのためには「光量子」を、「光の原子」つまり質量がわずかにある粒子と仮定して計算思考していくのが善策ではなかろうかというわけです。

この仮定(ルイくんは「仮定」どころか強く信じていたようですが)にもとづいて、彼は「光量子」は速度をゼロにすることも(計算上はですが)可能と考えます。そういうのを「光の原子」と呼び変えて、質量があるわけだからそれを「m₀」とおいてエネルギー換算すると…

一方この「光の原子」はアインシュタインさまのいわれる「光量子」でもあるから、そのエネルギーは…

「光量子」としてのエネルギーと、「光の原子」としてのエネルギーは等しいはずだから…
じゃーん

「光に質量なんてあるかっ!」「質量(ⅿ)ゼロなのになんで mc^2 になるんだっ!」と現代の皆さまは呆れることでしょうが、今はどうかこのオラの顔に免じて赦してやってつかあさい(CV: 野沢雅子)なにしろ百年前の論文、しかも著者はキレッキレの前衛フランス野郎・ルイくんですので。

これに続き、ルイくんさらに加速かけてきます。「ⅿ₀」で示したくだんの「光の原子」は静止状態にあります。これをですね、相対論の定めるこの宇宙における最高速度 c ぎりぎりまでスピードアップさせると…

左辺(赤でマーク)は「光量子」のエネルギー値です。プランク定数「h」を使って示したものです「hν」と。
(ちなみに「ν」は振動数。詳細は後で)
右辺(青でマーク)はアインシュタインの名高い「E=ⅿc^2」と同じものです。「違うやん」という方もいらっしゃるでしょうが、よく見てください青マークの上側にしっかり「m₀c^2」とありますよね。もとの質量「ⅿ₀」が光速に近づくほど増えていく様が、この右辺(青マーク)には仕込まれていて、そのぶん少しばかりごついのです。

「そうだとすると、宇宙における最高速度に近づくほど、右辺(青マーク)は無限に大きくなってしまうんちゃう?」と思われた方は鋭いです。
無限になってしまっては宇宙が壊れてしまうので、そうならないよう「宇宙最高速度に近づく」といってもわずかに遅いと条件を付けましょう。
この「わずかに遅い」についてルイくんは、「実験観測では測定できないほどわずかな遅さ」としています。そして「ⅿ₀」の質量も「ごくわずか」すなわちグラム単位でいうと「10^-50」(10のマイナス50乗)グラムぐらいだと算出しました。
ものすごく宇宙最高速度に近いけれどわずかに遅くて、質量もすんごく小さいと考えれば…

この等式は破綻しない!とはルイくんの弁です。
*
続く第二章を見ていきましょう。
「Ⅱ. The Black Radiation as a Gas of Light Quanta.」

「黒体放射を光量子気体と解釈してみよう」と高らかに宣言しちゃってますこのタイトル。
アインシュタインそれも無名時代の彼が、プランクの例の説(1900年)を読んで「そもそも光そのものが量子的なんちゃうか?」と考えたという話を前にしました。その閃きのもととなったのは、プランクも参照した「ウィーンの分布公式」がどういうわけか気体分子の式とよう似とるとアル・アインシュタインくんが気づいたことからでした。
当時のアル(1905年)のそういう思考過程を、1923~4年の頃のルイ・ド・ブロイくんがどこまで聞き知っていたのかはわかりません。そもそもアルはどの論文でも光と気体分子とのアナロジーについてそこまで立ち入っては述べていなかったと思います(後で調べてみますね)。ルイくんは異端さんだったので、同じく異端上がりのアルくんの思考過程を、知らず知らず辿っていたような気がします。
実際、目を通していくと「光の原子」を、気体分子と同じものと見立てて、マクスウェルの気体分子エネルギー分布則を当てはめてみたりしています。

本人にいわせると結果は「まあまあの類似」("an encouraging result, but not quite complete")でした。
光量子を、本論文第一章での議論を根拠に「光の原子」と解釈しなおして、気体分子の場合に使える数式を「光の原子」にも当てはめてみたらどうなるんやろう…第二章におけるこの企みは、現代の目で見るとやりすぎです。やりすぎですが、SF作家アーサー・C・クラーク卿いわく「可能かどうかの限界を見極める唯一の手は、その限界を少しばかり超越するまで挑戦することである」。ルイくんはこの第二章で(それから前年の論文中で)まさにそれに挑戦したのです、本人はそう考えてはいなかったとも想像しますが。
*
第三章いきます。「Ⅲ. An important Theorem on the Motion of Bodies.」

日本語にすると「物体の運動に関する、ある重要定理」。
第一章でルイくんは「光の原子」が、静止状態のときの質量を「m₀」と置いて、この「光の原子」が光速に近づくほど、相対論効果で質量が(僅かに)大きくなっていくと論じました。
その場合の「光量子」(「光の原子」をエネルギー的に呼び変えたもの)の振動数「ν」は、やはり相対論&光量子論によってこんな数式で計算できると、この第三章で述べていますね。
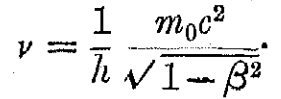
さらにはここまでシンプルにしてみせます。「ν₀」は「光の原子」が静止した状態のときの「光量子」としての振動数で、「ν₁」は運動状態のときの「光量子」振動数。

それにしてもいったいこの「振動数」とは、何がどう振動しているものなのでしょう? ルイくんにいわせると「光の原子」より何か波が生じていて、その波の振動が「ν」です。
「光の原子」が静止しているとき、その付随波の振動数が「ν₀」だとしたら、くだんの光原子が運動する(飛んでいくイメージ)とその速さにそって付随波の振動数は「ν₁」に変わると、そういう数式です上の数式。
ただ、このときの「ν₁」はどんな値でもいいというわけではなくて、以下の関係を満たしていないといけないそうです。

「ν₁」と「ν」で表される二つの波が、うまいこと重なり合うのは、この「=」関係が成り立っているときに限られると、そういうことです。相対論&光量子論の最強ペアではなく、高校で習う三角関数からちゃちゃっと導出できちゃう等式です。
このあとルイくん、ある波動現象について触れます。波長が極めて近いけれど同一ではない二つの波が合わさった時「第二の波」とでもいうべき波が生じる現象(これは実際にあります)について話をして「ぼくの波理論は、これと似とるねん」と自説のもっともらしさアップを図ってきます。
今の目で見ると「ああレイリー卿が19世紀後半に提唱したアレね。あれは正しい理論やわ。しかしそれとこれをこじつけるの、むちゃくちゃやわ」ですが、当時の彼は当時の最高の科学知識で精一杯誠実に「位相波」の正当化に努めたのでした。
*
ええと、この英語論文、前年1923年の三論文を一つにしたものが、第一章より第八章まで続きます。その後さらに章が複数続くのですが基本的に1~8章構成です。今回は3までご紹介しました。
とーじのひとでこれよんでわかるひと、そうはおらへんかったんやないかとあたしおもうわ。じかいにつづくよ。

