マックス・ボルンの1926年6月論文を読んでみよう（その４）

その３からつづくよ。前回触れなかった事柄に今回冒頭で触れますわ。

これです。$${αx+βy+γz>0}$$ な不等式。どうして０より大きいと条件付けられているのか？

これは原子に向かってまっすぐ跳んできてやがて軌道をカーヴさせて無限遠に去っていく電子の波動関数 $${sink_{nm}}$$ が、見てわかるように平面波つまり一番素朴な進行波であることと関係しています。$${>0}$$ と設定すれば、この進行波は一方通行であると数式におとしこめます。

「なーんだ」といわれてしまいそうな、ごくつまらない話です。前回触れていなかったので、今回補足的に触れておきます。

＊

こんな式が、この後でてきます。

実は私、これを目にして思いっきり頭を抱えてしまいました。

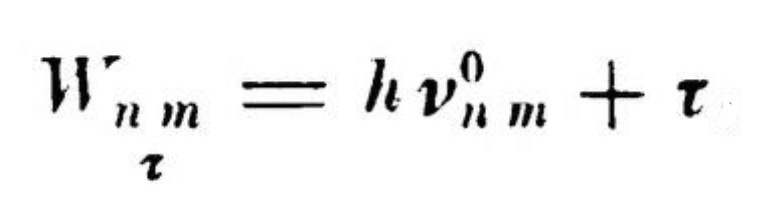
ボルン先生、赤で括ったブツについて「擾乱を受けていない原子の振動数」と論文中で説明しているのですが…

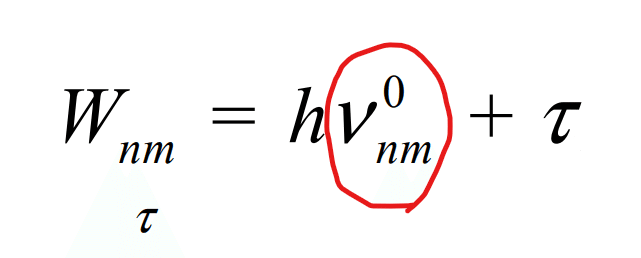
私はそれを「電子が無限遠から接近してくる『前』の原子の状態」と解釈していました。その解釈でいくと $${m}$$（「前」の量子数）と $${n}$$（「後」の量子数）をわざわざペアで付記する理由がわからないわけです。それで困ってしまったのですが…

よーく考えてみたら「電子が無限遠に去っていった『後』の原子の状態」と解釈しても、ボルン先生がいうところの「擾乱を受けていない原子の振動数」という定義とは別に矛盾しないのですね。

何時間も考え込んだ末にふとそれに気づいて、笑ってしまいました。とほほ。

それからこの τ（タウ）は、無限遠からやってきて、無限遠に去っていく電子のエネルギーのことなのは、前に説明した通りなのですが…

この式における τ は、無限遠に去っていくときの電子のエネルギーですね。

無限遠から接近してくるときのだと、思い込んでいたので、そうではないと気づいたときは、やはり笑ってしまいました。とほほ。

これもそうですね。電子が原子をフライバイして無限の彼方に向かって去っていくときの、両者の総エネルギーです。

要するにエネルギー保存則が成り立っているということです。

そのことを意識しつつ、先ほどのおっかなげな二重積分の式を眺めなおすと、この謎の φ について、その機能が見えてくると彼は言います。なんだと思いますか？

「電子がα, β, γで指定された方向（with 位相変化 $${δ}$$）に投げ出される確率を表す関数やー！」

この二重積分式において、無限遠からやってくる電子は $${z}$$ 方向からやってくると設定されています。（式にはそうはないのだけど論文中でそう設定されています）

それが原子との相互作用つまり干渉のし合いによって、電子の進行方向が $${(α, β, γ)}$$ に変わっていくのです。かくっと変わるのではなく、位置と時によって $${(α, β, γ)}$$ も変わっていきます。 

ボルン先生、ことばにはしていないのですがこの $${φ_{nm}(α, β, γ)}$$ （の下に $${τ}$$ が小さく添えられた）関数を二重積分すると $${1}$$ になると解しているようです。確率なのだから積分すれば１になるしかないよね、と。

それから原子に電子がフライバイする際に、電子のエネルギー τ も増減すると、そういう式であるぞと彼は喝破します、カッパ。

＊

論文（の予告編というべきかな）の終盤で、彼は励起（「れいき」と呼んでください変な風に読まないように）についてくどくど語ります。

励起ってわかりますか。原子の外部から何かエネルギーが注ぎ込まれると、それによって電子が外側の軌道に移るのです。

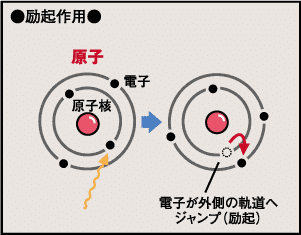
ボーア模型にもとづく図解です⇧ ボルン先生はこの模型をどうも鵜呑みにはしていないようですがここでは説明のためにこの図を使って説明しています私。

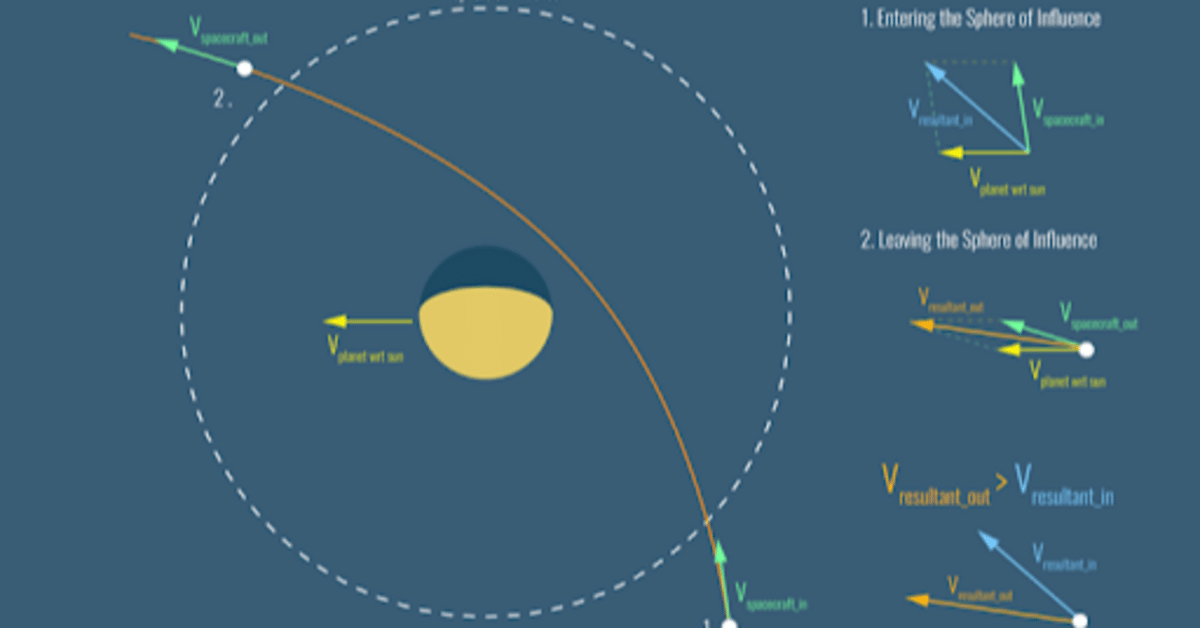
原子に電子がフライバイ（宇宙探査機がわざと惑星に接近して加速をかけて去っていく技です、本当は量子力学にこういう力学用語を流用するのはよろしくないのですが直観的に分かってもらいやすいので便宜的に使っています）する際に、原子の側で「励起」が起きるので、両者の総エネルギーは保存されるとしても、電子がどっちにどのくらいの速さやエネルギーで飛び去って行くのかを、宇宙探査機の軌道計算みたいに厳密には計算できない…そういうことをボルン先生、この論文の終盤で述べています。

「詳細は、後日掲載される私の論文をみてね」と。

＊

ここに注目！論文を書き上げて、そして掲載前の校正のとき、こんな注釈を彼は書き加えています。

「以下の関数の二乗が確率に比例する。詳しいことは次回のわしの論文みてちょ」と。

この予告どおり、彼は翌７月に、本編と呼ぶべき論文を寄稿することになります。