量子力学の教科書はどうしてこうわかりにくいのか？

コンビニではめったに買い物しない私ですが、公衆厠としては重宝しています。売店付きのレストルームですね。今どんなのが売れているのか、流行っているのか、流行らせようとしているのか、店内を歩くとなんとなくわかる気がするのです。店内に流れる「皆さんこんにちは、〇〇〇の▽▽▽▽です」の宣伝放送や、十代臭全開の恋歌とかが耳にとびこんでくるのもいい味です。書棚を見ると、ソフトカバーのプチ教養本が並んでいて、定番ものとしては日本海軍もの、中学英語から学びなおそうもの、相対性理論もの、それに量子力学ものがあります。表紙にアインシュタインのイラストがあれば相対論もので、猫のイラストがあったら量子力学ものというのがパターン。後者はいわゆる「シュレディンガーの猫」です。相対論にはアインというすーぱーすたーが付いているのに対し、量子力学には彼に匹敵する、大衆性のあるスターが欠けるのです。アルベルト・アインは、あの方程式「E = mc^2」に独りでたどり着き、さらに十年後には（ほぼ独りで）もうひとつの方程式（ここでは省略）に達して、並み居る当時の物理学者や数学者たちを出し抜いてみせたという、ロマンな香りがあります。しかし量子力学はというと、形になるまでいろいろな方たちが関わることになった、すなわち総力戦でした。そのぶん、"変人扱いにも屈せず彼は独りでこれを成し遂げた" 系のドラマ性は薄いのです。

ドラマ性が薄いというか、わかりやすいヒーローがいない、というかひとりにヒーローを絞れないのにはいろいろ訳があります。物理的難問は、しばしば哲学的難問でもあります。相対論はその筆頭でした。量子力学もそうです。その哲学的難問性は、相対論をしのぐものがあります。アルベルトが量子力学を嫌った（少なくとも不完全なものと考えた）のも、そこに相対論以上の哲学的わけわかんなさを見出したからでした。「何、確率がカギになる？ なにゆうてんねん神はサイコロ遊びはせえへん！」と言い放ったりね。これは正誤というよりは解釈問題なので、誰が勝利者なのか白黒つけようがないのです。中には「物理学者の国際会議でアルベルトを言い負かしてやったぜ！」と言いふらす方もいましたが、これはこの方の思い違いだったことが今は判明しています。（興味のある方は「アインシュタイン　ボーア」で検索してみてください）

ヒーローを絞れない理由に、さらにこんなのがあります。量子力学は、物理的難問、哲学的難問、さらには数学的な難問、それも二百年近く決着がつかないでいた難問への解答でもあったという点です。

個人的な履歴を少しばかり語ります。私はどちらかというと物理学徒系でした。どうして「系」と付けるのかというと、物理齧ってましたと胸張れるところまで行く以前に潰していただいたからです。今でいうパワハラ、アカハラ、ドクハラの三連同時攻撃でした。しかもワンオンワンでです。攻撃者はもうずっと前に亡くなっています。それはいいとして、カリキュラムから少々外れた道を独りでその後も紆余曲折右往左往し続けたことから、数学徒っぽいところも自分にはあります。そのおかげで、量子力学を数学的言語で語るにあたってカギとなる「固有値」の考え方について、物理学者というよりは数学者の目線で眺める目線を育みました。

これはその昔、かのオイラーも巻き込む論争から生まれてきたものです。いわゆる「弦論争」。弦を指ではじくとびーんと震えますよね。これを微分方程式で記述するにあたって、指で弦を持ち上げてぱっと離す瞬間については方程式で扱うべきなのか、それは除外すべきなのかという論争です。わけわかんないと思いますがヨーロッパの当時の最高の数学者たちが論戦した難問です。エカテリーナ女王とかフリードリヒ2世とかの啓蒙君主の時代のことでした。これについて決着がつくのはもっと後の時代になってからでしたが、それより前にこの「弦論争」からもうひとつ面白い数学が生まれてきました。弦が揺れるとは、要は波うつということです。振動の波の長さは変わらない。簡単にいってしまえば、波の長さが変わらない現象が数学でいう「固有値」にあたるものです。微分方程式の研究から浮かび上がってきたものでしたが、もっと後の時代になって積分方程式の研究が進むにつれてこの「固有値」がやはりカギになるとはっきりしてきました。ちなみにこの時期は、今でいう行列の研究の大発展期でした。行列式ってわかりますか？ あれを巧く使うと、積分方程式を解くのに「固有値」を介して行列が使えることがはっきりしたのです。これは２０世紀の頭ぐらいの動向だったかな。

行列を使って積分方程式が解けるということは、さらに進んで行列を使って微分方程式を解く技が編み出せるんやないか？と気づく数学者が現れました。ヒルベルトって名前、どこかで目にしたことはないでしょうか。ダフィット・ヒルベルト。独逸人。数学者。行列が微積に活かせるということは、微積とともに発展してきた物理学を、さらに行列を導入することによってもっと高度に数学化できるやないかと考えたのです。彼は幸運にも、物理学にも精通した同僚ミンコフスキーに恵まれました。この方を質問攻めにして物理学の最新の課題をどんどん学び取り、今でいう数理物理学の開拓に乗り出したのです。弟子筋の方が書籍化しました。邦訳もあります『数理物理学の方法』。原著（ドイツ語です）第一巻が出たのが1924年ですので、おお、量子力学の誕生前年やないですか。今でいう線形代数の飛躍的進歩を追い風に、物理学を数学者の手で革新したれという意欲を感じます。ヒルベルト曰く「物理学は物理学者には難しすぎる」（„Die Physik ist für die Physiker eigentlich viel zu schwer.“）

翌1925年、物理学のほうで、原子における電子の軌道をめぐって面白い論文が出ました。花粉症で熱を出してしまって海岸療養中だった若きハイゼンベルクが、半ば思い付きで繰り広げた説です。詳細は省きますが、この論文を送られた彼のお師匠ボルンは「またわけわからんことを言ってきたぞあの落第すれすれ男が…むむ、まてよ、こいつの論文には Σ（シグマ）と数列がぎょうさん出てくるな…どっかで見たことがあるような…そうかこれって行列やんか。行列は多少ひとから聞き知っているし、あいつに代わってもうちょっと式を整理したるか」と重い腰をあげました。ただこの時代は行列は数学の前衛でしたので、物理畑のボルンには少々手に余るものでした。そこで教え子のひとりに、数学大得意なヨルダンというひとがいたので「ちょっと手伝ってえや」「ええですよ」と抱き込んだのです。このヨルダンくんは、ヒルベルトの『数理物理学の方法』第一巻の編纂にも関わっていたひとで、物理学と数学のいってみればバイリンガル的な若者でした。師匠ボルンを手伝って、ハイゼンベルク論文を行列で書き替えることに成功。その後ハイゼンそのひとも巻き込んで、ボルン、ヨルダン、ハイゼンの三人共著論文ができあがりました。1926年のことです。これが量子力学の、数学として整ったものの最初となったのでした。

その直後に違う物理学者シュレディンガーによって違うやり方による同じ解答導出法が提示されて物理学界大波乱となりました。シュは微分方程式を使って、原子における電子の軌道を説明したのです。ハイゼンらは行列を、シュは微分方程式を使っていました。違う数学を使っていて、なんで同じ答えがでるんや須藤！ 物理学者たちは頭を抱えました。ハイゼン一派の大親分ボーアとシュレディンガー（そういえばこの二人、たしか同い年）が文字通りの死闘を繰り広げたものの決着つかずでシュがボーアの目の前でとうとう寝込んでしまうなんてこともあったり。そこにさらにボルンが乱入して「シュレディンガーの説はここがおかしい、この式はこう解釈すれば観測事実と整合するんちゃうか」と言い出したおかげで、さらに学界大波乱。そこに今度はディラックという若者がえげれそから現れて「こういう技が電気工学にあるんやけど、これ使えばシュとハイゼンの技に橋架かるで」と切り出したせいでもっと大混乱。デルタ関数という、電気系の技でした。数学者にいわせれば「そんな工学系の緩いもん関数と呼べへん」な関数でした。

翌1927年、数学者フォン・ノイマンが、この大混乱から少し距離を置いたところからスマートに議論を整理してみせました。「量子力学の数学的基礎」という論文です。独逸語です。物理学者たちがそれぞれに編み出した技や解釈を、ひとつの数学的体系にまとめあげた論文です。この体系化にあたって、彼は師匠ヒルベルトにちなんで「ヒルベルト空間」という数学的概念を提唱しました。これは彼がひとりで作り上げたものではなく、数学における行列研究の、ひとつの集大成的なものです。頭の中に図書館が内臓されていて、読んだ本はすべてそこに収納されていて一字一句閲覧できたという、通称「火星人」な彼らしい、究極の秀才論文というところでしょうか。

これは数学のジャンルをひとつ作り出した（少なくともまとめあげた）といっていい、壮絶なものでした。彼はたしか当時23歳？ おえ。このスーパー数理物理の登場によって、物理学者たちの混乱も収まった…とはことが進まなかった。当時、量子力学に関わった物理学者たちが、いったいどうノイマンのこの論文を読み、理解したのか、あるいは理解しぞこなったのか、私にはとても興味があります。どうもそこのところが科学史の書物を追っても、当時の物理学者たちの論文を検索で探し出して目を通しても、はっきりしないのですね。ひとつはっきりいえるのは、量子力学の確立に血眼になっていた当時の物理英才たちは、このヒルベルト空間の考え方については敬して遠ざける姿勢に傾いたことです。現代の量子力学の教科書にいろいろ目を通すと、それを感じます。うまくいえないのですが、いちおうそれに言及はしている一方で、それに極力軸足を置かないように話を進めていくのですよ。たとえばブラケット記号とかディラック記法とか、私にいわせるとヒルベルト空間からできるだけ距離を置くために発案され、重宝されているように私には思えてなりません。それでいてこの記法を使って単位の分解だの共役作用素だの、つまりノイマンが数学言語で提唱した事柄を語るのです。なんというか、中国語の作文を「漢文」として読んでいくような、変てこな感じです。レとか一とか二とかの、変な記号を文にくっつけてね。李白や孔子（の弟子たち）がそうやって詩を詠んだり文筆を残したりしたわけやないでしょとも思うわけです。

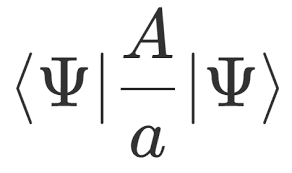
漢文を習うのと、中国語を習うのを、同時進行でやらされる…量子力学の教科書のわけわかんなさは、比喩ですがこれなんじゃないかなって気がしています。