
連鎖時計パズル
この記事は日曜数学 Advent Calendar 2024の8日目の記事です。
どうも、108Hassiumです。
今年に入ってからWolf RPGエディターというソフトでフリーゲームを作り始めました。
制作したものは今のところ全て脱出ゲームなのですが、脱出ゲームといえば謎解きが欠かせません。
なので制作期間の内の結構な割合を謎解きのアイデア出しに費やしたのですが、そんな中で数学的にちょっと面白そうなパズルを発見(?)しました。
というわけで、この記事ではそのパズルについて解説します。
※あくまでも「なんか面白そうなもの見つけたよ」という趣旨の記事なので、あまり踏み込んだ話はしません。というかできません。
※前例の有無は調べていません。
基本説明
「連鎖時計パズル(仮称)」は、こんな見た目のパズルです。

床の上にいくつかの時計が置かれており、主人公が時計を調べることで針が動きます。
針は基本的には90度ずつ動くのですが、動いた直後の針が指す先に別の時計があればその時計の針も動きます。

時計を特定の状態(例えば「全部下向き」等)にすると宝箱の鍵が開く、という形でゲームに取り入れようと思ったのですが、実際に触ってみるとゲーム的な意味ではあまり面白くなかったので没にしました。
さて、まず気になることと言えばこれです。
疑問1:全部の針が上を向いている状態から到達不可能な状態ってどんな状態?
※以下、全部の針が上を向いている状態を「標準初期状態」と呼ぶことにします。
以下のような複数の時計が互いに指し合っているような状態は、到達不可能であることが簡単にわかります。

しかし、このような簡単に判別できるパターン以外に到達不可能な状態が存在するかは不明です。
連打
適当に遊んでいたところ、「標準初期状態から左上の時計だけを動かし続けると、24回で初期状態に戻る」という性質を発見しました。

では他の時計だとどうなるか、と思って調べてみたところ、どの時計でも24回調べると標準初期状態に戻るようでした。
ちなみに、右下の時計を連打したときの結果は左上の場合の図をよく見れば実験しなくてもわかります。
まず、連鎖時計パズルには「『時計を動かしてから盤面を回転させる』と『盤面を回転させてから時計を動かす』という操作の結果は等しい」という性質があります。

※以下、「盤面」という単語は時計の配置とそれぞれの状態と操作箇所の組み合わせを指すものとします。
そして、標準初期状態から左上の時計を連打し続けると6回目で全ての時計が下を向く、つまり標準初期状態を180度回転させた状態になります。

ということはこの後の遷移は「標準初期状態から右下を連打したときの盤面を180度回転させたものの遷移」を表していると解釈することができ、右下を連打したときも24回で標準初期状態に戻ることがわかります。

一方で、右上と左下を連打した場合についてはこのようなわかりやすい対応関係は見られませんでした。


さて通常の2×2の配置について「標準初期状態から1個の時計を連打して標準初期状態に戻るまでの操作回数」が求まったわけですが、これとは違う時計配置や変則的なルールの場合は「標準初期状態から(中略)操作回数」はどうなるのでしょうか。
※以下、各時計についての「標準(中略)回数」のことを「位数」と呼ぶことにします。
まず、シンプルな例として時計が横一直線に並んでいる配置を調べてみました。

どうやら位数は必ずしも4の倍数になるわけではないようです。

配置によっては位数の異なる時計が混在することもあるようです。
なお、1×3のような配置では針が指す先に複数の時計がある状況が発生しますが、その場合は隣接する時計1個だけが動くものとしました。



疑問2:1×2nの時計配置ではどの時計も同じ位数になるの?
続いて、一直線型の配置を折り曲げたL字型の配置を調べました。



折り曲げる前の配置での位数と同じになりました。
続いて、次のような変則ルールについて調べました。

左右の端を繋ぐ線は新たに追加された接続関係を表しており、具体的には
左の時計の針が左を向いていたら、右の時計を指していることにする
右の時計の針が右を向いていたら、左の時計を指していることにする
・・・というルールが追加されていることを表します。
この変則ルールの下では1×nの直線状配置における位数は、nが奇数でもn個全て同じ値になります。
というわけで、実際の位数の値は以下のようになります。
n=2→6
n=3→10
n=4→24
n=5→38
n=6→90
ここで注目してほしいのはn=4のときで、「4個の時計の位数が全て24」というのは先述の2×2の初期配置と同じです。
先程のL字配置と合わせて考えると、このことは以下のようにまとめることができます。
疑問3:接続関係を表すグラフが同型であるような初期配置は、位数の組み合わせも同じになるの?
ここでの「グラフ」というのは点を線で結んだ数学的構造物のことで、関数や方程式の可視化手段のグラフとは別物です。
グラフは線による点と点の繋がりを表すものなので、点の位置関係や線の長さ等が違っても繋がり方が同じなら同型(同じ形のグラフ)と見做されます。


2×2配置と両端繋ぎ1×4配置、1×n配置とそれを曲げたL字配置は接続関係のグラフがそれぞれ同型になり、位数の組み合わせも一緒でした。
これと同じように、接続関係のグラフさえ同型であれば異なる時計配置でも位数の位置関係が一致するんじゃないか、というのが疑問3の内容です。
位数に関してはこれ以外にも色々気になることがあるのですが、キリがないので大事そうな疑問を2つ投げて終わります。
疑問4:任意の時計配置に対して全ての時計の位数を効率よく(実際に連打するより簡単に、できれば手計算で)求める方法は?
疑問5:位数が無限(連打しても標準初期状態に戻ってこない)の時計が存在するような配置って無いの?
※接続関係を付け加えた時計配置の場合、標準初期状態に「時計が互いに指し合っている部分」が含まれることがあるので、そのようなケースは除外します。
可換性
連鎖時計は、「ライツアウト」という古典(?)パズルの変種であると考えることができます。
ライツアウトやその変種の数学的分析において重要そうな概念として、「操作の可換性」というものがあります。
ライツアウトでは2か所のライトを1回ずつ操作する場合、操作する順序によらず操作結果は同じになるという性質があり、この性質を「可換」と呼ぶことにします。

そして、どういう訳か連鎖時計でも可換性が成り立つようです。
疑問6:連鎖時計の操作って可換なの?
ライツアウトの可換性に関しては少し考えれば「ああ、確かに成り立つな」となるぐらいの話だと思うのですが、連鎖時計の可換性はかなり非自明な気がします。
ちなみに、可換性の話は位数の話にも少し関係があります。
位数は「標準初期状態から標準初期状態に戻ってくるまでの操作回数」によって定義していましたが、操作が可換であれば「標準初期状態から到達可能な状態」を初期状態としても位数と同じ操作回数で初期状態に戻ります。

ただし、標準初期状態から到達不可能な状態の内「複数の時計が互いに指し合っているような状態」は何回操作しても元に戻りません。

最長連鎖
冒頭の基本説明では、時計の針が合計9回も動く長大な連鎖パターンを動作例として紹介しました。

これより長い連鎖パターンが存在するかどうかが気になったので、検証方法を考えました。
まず、盤面の回転に関する性質により、ある盤面を回転させた盤面の連鎖数は元の盤面と同じになるはずです。

ということは最長連鎖の盤面も向きが違うだけのものが4つずつ存在するので、「最後に動く時計が左上の時計であるもの」が必ず存在するはずです。
というわけで、こんな図を描いてみました。

これは左上で終わる連鎖を逆向きに辿った樹形図です。
ある盤面の右にはその盤面の1ステップ前の盤面が接続され、右側に何もない盤面は前の盤面が存在しない(=連鎖の開始時点にしか現れない)詰み状態の盤面になっています。
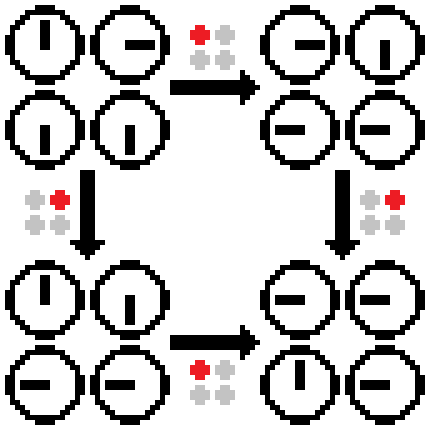
例として、以下の盤面の前の盤面が何か考えます。

赤い時計は動く直前の時計で、針の無い時計は向きが未確定の時計を表しています。
この盤面の前の盤面を考えるには、赤い時計がどの時計から指されたかを考える必要があります。
まず、右上の時計は赤い時計を指しているので、この時計が動いて右下の時計を指した可能性があります。
また、左下の時計は向きが未確定なので、この時計が動いて右下の時計を指したというケースも考えられます。
というわけであの盤面の直前の盤面は、右上の時計が動く盤面と左下が動く盤面の二種類が存在し、樹形図は以下のようになります。

この後は、右上が動く方の盤面は赤い時計がどこからも指されないので詰みになり、左下が動く方は右下の時計から指されるパターンがあるのでさらに樹形図が横に伸びます。
さて、最長連鎖の話に戻ります。

図中で一番右にある盤面が最長連鎖の盤面(の内、左上で連鎖が終わるもの)で、冒頭の動作例の図で示したものを90度回転させた盤面であるため、結局あれより長い連鎖は存在しないことがわかります。
2×2の盤面の解析はこんな感じで非常に簡単だったので、3×3でも同じ調査をしてみました。
まず、3×3での連鎖の終わり方(位置と向きの組み合わせ)は以下の3種類に分類できます。

※以下、各パターンを左から順にパターン1~3と呼ぶことにします。
そして、各パターンに対応する樹形図は以下のようになりました。



それぞれの図における連鎖を比較することで、パターン3に該当する以下の盤面が3×3の最長連鎖であることがわかります。

ところで、樹形図を描いている最中に連鎖長以外に気になったことがありました。

樹形図のステップごとの横幅が、途中からなぜか広い部分と狭い部分が交互に並んでいるのです。
先程の図を見直してみると、3つの樹形図全てでこの現象が起きていることがわかると思います。
この現象についてもう少し調べてみようと思ったのですが、「樹形図の横幅」という概念は人工的過ぎて(?)扱いにくかったり面白みに欠けていたりするような気がしました。
というわけで、別のデータにも似たような現象が現れていないかと考えました。
樹形図の横幅は「ステップごとの盤面の個数」や「詰んだ盤面の個数」、「分岐の発生回数や頻度」等の要素から影響を受けるので、それぞれの値を調べてみました。


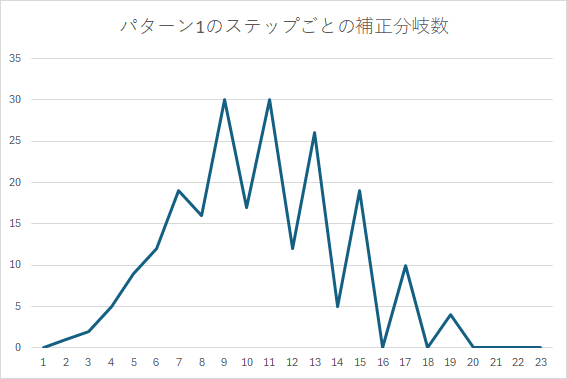
どのグラフもかなりはっきりと振動しているのがわかると思います。
なお、最後の「補正分岐数」というのは、次ステップの盤面数から「盤面数-詰み盤面数」を引いた値です。
分岐の個数に対して「三又分岐と四又分岐をそれぞれ分岐2つと3つとする」という補正を加えた値と解釈できるので「補正」という単語を使ったのですが、「分岐の個数を直接数えてからそれを補正した値」ではありません。(分岐の個数を直接数えるのは面倒臭すぎるので諦めました)
パターン2・3でも同様の現象がみられるのですが、3パターン分のグラフを重ねてみると新たな発見がありました。

パターン2とパターン3の振動の位相(山谷の位置)が明らかに異なっており、パターン1と位相が合っているのはパターン2の方です。
このことから、盤面数などの振動現象の原因に関する以下のような仮説を思いつきました。
まず、3×3のマス目を市松模様に塗ります。

すると、9つあるマス目は色の違いにより「辺の位置にあるマス目」と「角と真ん中のマス目」の2種類に分かれます。(以下、それぞれ黒マス・白マスと呼ぶことにします)
「連鎖は隣接する時計にしか伝播しない」という性質により、3×3の樹形図では「赤い時計が黒マスの位置にある盤面」と「赤い時計が白マスの位置にある盤面」が横方向に交互に並びます。

ここで、「3×3のマス目における隣接するマスの数」を数えてみると、黒マスは3つずつ、白マスは平均すると2.4マスになります。
隣接するマスが多いという事は「赤い時計が移動する際に、黒マスから白マスに移動するときの方が『移動できる可能性のあるマス』が多い」という事を表しています。
このことから、黒から白への移動の方が分岐が発生しやすく、詰みが発生しにくく、盤面数が増えやすく減りにくく、結果としてそれぞれの数値が振動するのではないか、ということが予想できます。
そして、パターン1・2とパターン3で振動の位相が違ったのは、連鎖の終わる位置がパターン1・2では白マスで、パターン3だけは黒マスだったからだと考えられます。

疑問7:樹形図の盤面数や詰み数、分岐数とかの振動って、時計配置を市松模様に塗った時の色ごとの隣接するマスの数の差によって起きるの?
この仮説が正しければ、正方形の時計配置では以下のようなことが起こると予想できます。
4×4の樹形図では、盤面数等の振動は起こらない
奇数×奇数の樹形図では振動が起こるが、サイズが大きくなるごとに振動は弱くなる(隣接するマス数の差が小さくなるので)
いずれにせよ、樹形図を描いてデータをとるのが大変過ぎて検証はまともにできそうにないです。
疑問8:任意の時計配置に対して最長連鎖の盤面を効率よく求める方法は?
疑問9:任意の時計配置に対して樹形図の盤面数や詰み数を効率よく求める方法は?
最長連鎖の盤面は樹形図を描くよりかは賢い方法がありそうですが、樹形図の統計データに関してはどうにもならないような気がします。
定義通りに愚直に計算するにしても計算を自動化できれば手作業よりは遥かにマシになると思いますが、残念ながら私はそこまで賢くないのでできることは少なそうです。
最後に
明日の日曜数学 Advent Calendar 2024の記事はT.さん記事で、内容は「たぶん多項式のGCD関係」とのことです。
おまけ
試遊
連鎖時計パズルを実際に動かせるようにしました。
https://plicy.net/GamePlay/194464
ブラウザ上で動作しますが、スマホは未対応です。
没図


用意したけど最終的に使わなかった画像です。
宣伝
高難度脱出ゲーム「サーモンピンク鬼」&「エメラルドグリーン鬼」は
の3サイトで好評配信中!!!
