
アインシュタインタイルの配置パターンから”琵琶湖の水”を全部抜いて愛でてみる。とにかく愛でてみる。
前回のシリーズの記事はこちら。
この記事を書いたあと、ふとあることを思いついてやってみると「沼」でした(琵琶湖じゃないんかい)
では、ぬかるみっぷりをお伝えします。
配置パターンは「滋賀県」
前回、アインシュタインタイルを構成する辺2種類を(以下のような感じで)描き分けてみました。
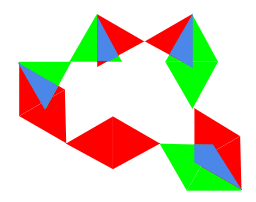
この図形をSPECTREの配置パターンにあてはめると、中央のタイルが他のタイルとは全く逆の種類の辺に接していることがわかりました。

赤:赤、緑:緑ではなく
赤:緑で接しています。
これと同じように、HATの配置パターンでもあてはめてみると、中央のタイルは他のタイルと同じように、同じ種類の辺で接します。
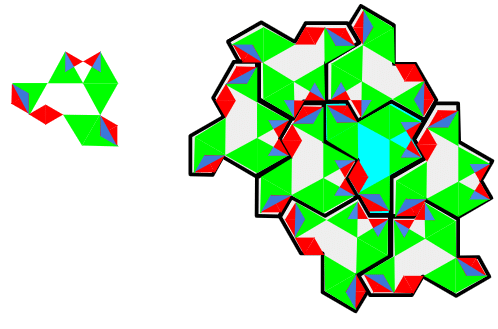
配置パターン(H₈)にあてはめると、
赤:赤、緑:緑で接しています。
ところで、HATの配置パターンだと他のタイル――TURTLEとかTile(x,y)いろいろ――も同様になります。
いってみれば、配置パターンにあわせてタイルを変形させても同様になります。
じゃあ、SPECTREの配置パターンでもできないかと考えてみました。
SPECTREだと中央のタイルが異なるので、抜いてみることにしよう。
HATの配置パターンだと、

こんな感じ。
抜いたタイルを「琵琶湖」に例えれば、配置パターンは「滋賀県」です。
HATの配置パターンでタイルを変形すると、中央の水を抜いた穴は、変形したタイルと同じ形(の裏返し)になります。
HATとTURTLEはどこまでも仲良し
Tile(1,1)でSPECTREの配置パターンをつくり、中央のタイルを抜きます。
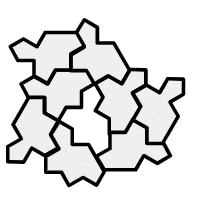
Tile(1,1)をHATに変えてSPECTREの配置パターンにならい並べてみると、下のようになります。
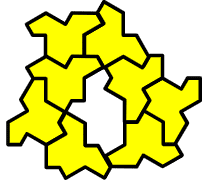
抜いた穴の形はTURTLEでした。
あれ?
じゃあ、TURTLEでSPECTREの配置パターンで並べてみますか。
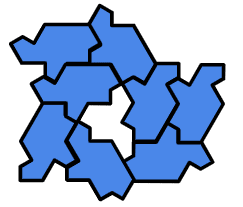
ぎゃあぁぁぁぁす!!!!
抜いた穴の形はHATじゃないかい。
ちなみに、HATのSPECTRE配置パターンに2種類の辺描き分けタイルを置いてみると、
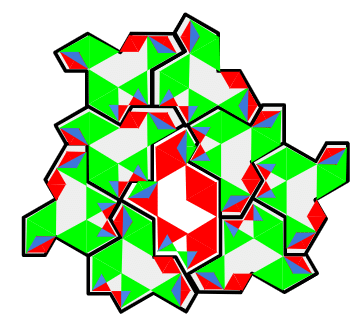
HATのタイルと中央の穴のTURTLEとの接し方が赤:緑となっております(そうなるんですが)。
そうすると、SPECTREが正しい(10月現在、精査中で未確定)とすると、HATとTURTLEの2種類1セットにした、非周期的敷き詰めの配置パターンがあるのでは、となります。
配置パターンってどうなるの?
論文「A chiral aperiodic monotile」の6ページ(Figure2.1)をもとにして、HATとTURTLEをあてはめてみます。
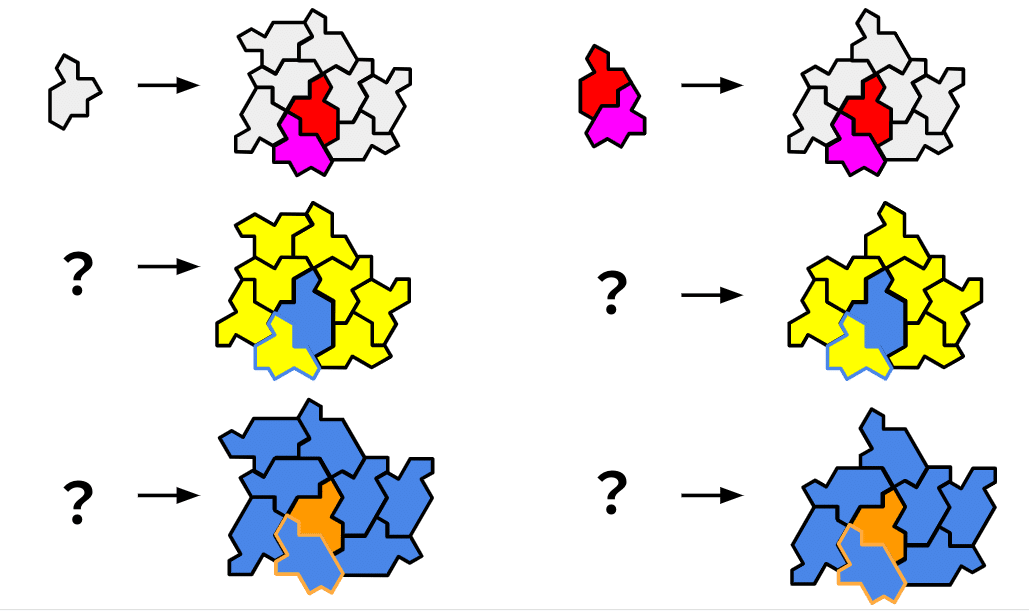
上の図がSPECTREの配置パターン。
中の図がHAT、下の図がTURTLEであてはめたものです。
ここで悩ましいのが、配置パターンの左側に入る図形(タイル)です。
なにせSPECTREの配置パターンは、単に複数のタイルを組合せているだけではなくて裏返しているのです。
その点を考慮しなくてはならない。
あれこれやってみて、ここであいつらが登場します。
ヘリコプターです。

このタイルを使って、配置パターンに並べてみます。
すると、以下のように左側が判明します。

描いてみるとわかったことがあります。
SPECTREの配置パターンですが、(回転主翼の向きが変わらないということは)タイルを裏返すのではなく、(回転尾翼の形状を変えて)タイルを変形させています。
Tile(1,1)は、変形しても同じ形になるので気づかなかった……のか。
HAT、及びTURTLEの配置パターンは、中→中→中→……とか下→下→下→……の繰り返しではありません。
……→中→下→中→下→……と交互に使用(ただし、回転主翼の向きを合わせるので、交互に裏返しが発生)していきます。
……で、いいんですかね?
間違えてたらごめんなさい、ホント。
とりあえずの締め
ということで、なんかいろいろなことになっている記事でした。
アインシュタインタイル、まだまだ遊べますね。
困った困った。
次回はせまゲーをやるので、次々回の予告。
せっかくなので、ヘリコプターのタイルをSPECTRE配置で敷き詰めることにしました。
すると、こんな感じ。

色分けしましたが、見事に回転主翼の正三角形群生地帯が発生しました。
これをちょっと追ってみます。
では。
