
アインシュタインタイルTile(1,1)の配置パターンを愛でる。とにかく愛でてみる。
前回の記事はこちら。
前回やり残した、Tile(1,1)の配置パターンにまいります。
H7・H8も確認
おさらい的ではありますが、Tile(1,1)の場合のH7とH8を見ていきます。
H7、H8は論文「An aperiodic monotile」の18ページにある、「HAT」などのアインシュタインタイルを複数個(H7は7個、H8は8個)組み合わせたユニットになります。

Figure 2.11
https://doi.org/10.48550/arXiv.2303.10798
下の図が、Tile(1,1)のH7(左)とH8(右)になります。

H7を120度、240度回転させて重ねると、以下になります。
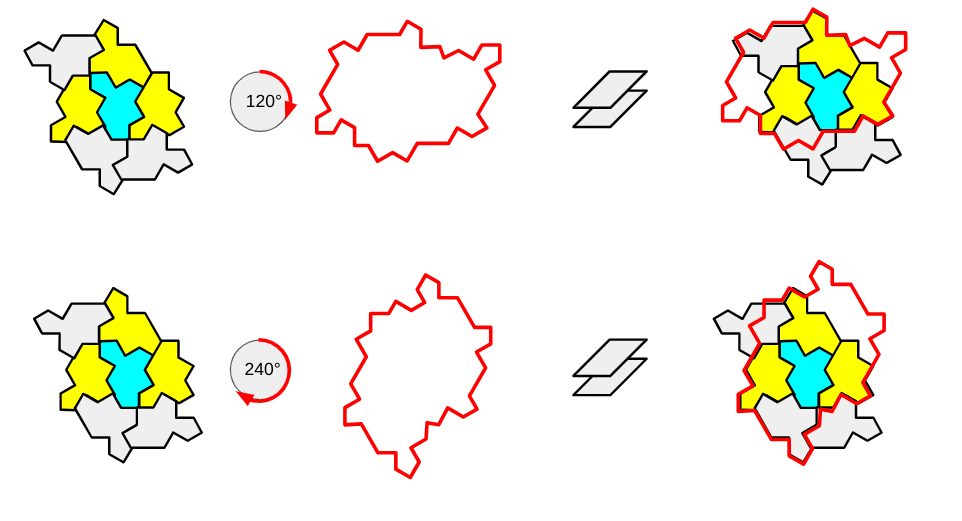
H8を120度、240度回転させて重ねると、以下になります。

ほぼ、前回と同じような見た目なので、駆け足ですすみました。
では、H7とH8を180度回転させて重ねます。

ということで、120度・240度回転重ねでは、下左図の2つの点対称図形に分かれるヘリコプターとなり、180度回転重ねでは、下右図のまた異なる2つの点対称図形に分かれるヘリコプターとなります。

ちなみに、右の図はもう1つ回転尾翼(青)を追加すると、バットマンマークっぽくなります。

この図形は、周期的に敷き詰めることができます。

「SPECTRES」の配置パターン
「SPECTRES」の配置パターンは、論文「A chiral aperiodic monotile」の6ページ(Figure2.1)、および7ページ(Figure2.2)にあります。

Figure 2.1
https://arxiv.org/abs/2305.17743

Figure 2.1
https://arxiv.org/abs/2305.17743
この配置パターンの扱い方について、日本テセレーションデザイン協会代表の荒木義明さんのツイートがあります。
新論文のFig2.2の置換システムはちょっと不思議。
— Yoshiaki Araki 荒木義明 (@alytile) May 30, 2023
初期値は一匹の亀。次のステップで全部を裏にしてから並べています。このうち緑の亀だけ30度分ズレている。
この30度のズレは前回の非周期タイリングには現れない置き方で、これが今回の鍵なんだろうか?青は論文の薄緑に対応https://t.co/aMpssYyKTk pic.twitter.com/9DgHIhiXGR
【引用】
新論文のFig2.2の置換システムはちょっと不思議。 初期値は一匹の亀。次のステップで全部を裏にしてから並べています。このうち緑の亀だけ30度分ズレている。 この30度のズレは前回の非周期タイリングには現れない置き方で、これが今回の鍵なんだろうか?青は論文の薄緑に対応
ちなみに緑と青の亀の塊を「Mystic」(神秘?)と呼ぶそうです。さて置換システムの2回目では9匹の亀の塊を8つ作り全部裏にして並べます。このときピンク色の部分が1箇所重なります(ナゼ!) pic.twitter.com/OeFSY6o4fW
— Yoshiaki Araki 荒木義明 (@alytile) May 30, 2023
【引用】
ちなみに緑と青の亀の塊を「Mystic」(神秘?)と呼ぶそうです。さて置換システムの2回目では9匹の亀の塊を8つ作り全部裏にして並べます。このときピンク色の部分が1箇所重なります(ナゼ!)
あとはこの繰り返しで、先の塊を8つ複製して全部裏にして並べます。このとき黄色の塊が1箇所重なります(そして外形はフラクタルになっていく) pic.twitter.com/tVbwsSiMD9
— Yoshiaki Araki 荒木義明 (@alytile) May 30, 2023
【引用】
あとはこの繰り返しで、先の塊を8つ複製して全部裏にして並べます。このとき黄色の塊が1箇所重なります(そして外形はフラクタルになっていく)
どうやら、いちいちタイル全部裏返してから、配置パターンを用いてどんどん拡大していくようです。
なんで裏返すのでしょうかね?
双方の配置パターンを見比べる
「SPECTRES」の配置パターンですが、これらは先の論文の配置パターンH7とH8とどれくらい似ているのか、確認してみます。

左のパターンはタイル8個の組み合わせなので、H8と同じタイル枚数。
右のパターンはタイル7個の組み合わせなので、H7と同じタイル枚数、となります。
右側の配置パターンをちょっと動かしてみます。

左図が配置パターンです。
水色と黄色のタイル1組は「MYSTIC」とよばれます。
黄色のタイルを一旦外しまして(中図)、水色のタイルを残りのタイルに当てはまるように裏返します(右図)。
H7の配置パターンには裏返したタイルが1枚あるので、このタイルを目印として比較します。
H7を裏返しのタイルに合わせて角度を調整し、2つの配置パターンを並べると、このようになります。

右:H7
7枚中5枚が一致しました。
異なる箇所を抜き出したのが、以下の図です。

もう1つの「SPECTRES」配置パターンとH8と比べてみると、8枚中6枚が一致し、異なる箇所もまた先の見比べたものと一致します。

一番上にあるタイルを0度とした、それぞれのタイルの向きは以下の図のようになります。

右:H8(左上のタイルを除くとH7になる)
なぜ裏返す?
しかし、「SPECTRE」配置パターンは、いちいち裏返すのか、不思議ですね。
以前の記事「アインシュタインタイル「SPECTRES」を愛でる。とにかく愛でてみる。」で、こんな図を書きました。

「HAT」と「TURTLE」は(回転主翼(黄色)が鏡像の)対の関係になっている図です。
前回の記事「アインシュタインタイル配置パターン「H7」「H8」を愛でる。とにかく愛でてみる。」でも、「HAT」と「TURTLE」が対関係であることを垣間見ました。
「HAT」の非周期的敷き詰めで出てくる裏返しのタイルは、実は対となるタイル「TURTLE」と関係していると思います。
Tile(1,1)は、対となる関係の図形はありませんが、以前の記事「アインシュタインタイルTile(1,1)を分割して愛でる。とにかく愛でてみる。」で、分割次第では、対になる分割ができました。

配置パターンで裏返すのは、「HAT」と「TURTLE」との対関係にある図形に似たもつれをほどくため、かも知れません。
締め
ということで、ざっくり配置パターンを愛でてみました。
論文にドップリ浸からず、浅くサラリと眺めています。
一貫して、本当にたいしたことを書いていません。
とりあえず、ここで一区切りにして落ち着くことにします。
他の記事も書かねば、と若干焦っております。
では。
