文系のための、超基本数学講座

こんにちは。

昨日更新するのをすっかり忘れてしまっていました。

さて、文系の皆さん、なぜ文系を選択しましたか？
色々理由はあると思います。法律を学びたい、経営を学びたい、歴史が得意、などなど。
しかし、かなりの人が「数学が苦手だから」という理由で選んでいるのを知っています。

しかし、経済学部や商学部など、数学を使う文系科目は実はかなり多く、定期テスト前にひーひー言っているのをよく見ます。
あるいは、「数学得意だったけど文系行ったわｗだから数III知らへんｗ」みたいなカスみたいな自慢をしている人をよく見ます。

今日はそんな、文系なのに大学の定期テストでがっつり数学をやらなければならない人たち、および(私怨で)数IIIすらやってないのに数学得意を自称する不届き者たちに向けた、超超基本の数学講座を行いたいと思います。

はじめに

扱うのは数IIIが多いと思います。
この数III、文系からは恐れられているみたいですが、理系からするとわかってなければありえないレベルの超基礎の基礎の基礎なので、これぐらいは把握しておきましょう。

はっきり言って、数IIIで習うものの中には「これ分かっていないで数学って、何ができるの？」みたいなレベルのものをかなり含むのです。
今回はその「これ分かっていないで数学って、何ができるの？」枠が中心です。なのでこの記事をまず完璧に理解することを優先してください。

e, log

たぶん理系の人たちはまさか文系の人たちがこれを習っていないとは思わないレベルの基礎中の基礎です。
この二つが分からないと本当に何もできません。

まずはeについて。下式が定義です。

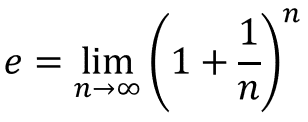
定義を見てもさっぱりだと思うので説明します。
小学校の時円周率を3.14として計算してたと思いますが、中学以降はπを使いますよね。あれと同じで、本当はめちゃくちゃ長い小数なんですが、それをeという文字であてがっています。
通称ネイピア数といいます。

なんでこんなわけわからんのを文字として置いているかというのは次項で詳しく説明しますが、非常に便利な性質をたくさん持っているからです。
そしてeで表される関数というのは大変に多く、例えば経済学部なら統計という科目を習うと思いますが、おそらく10ページ目ぐらいにはeが早速出てきます。
詳しいことは省きますが、最も基本的な確率分布である正規分布の確率密度関数が下式のようにeを用いて表されるからです。

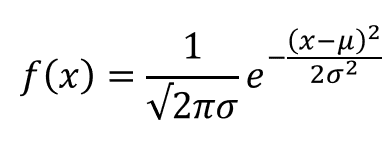
安心してください。覚えなくていいです。
この小難しい関数を覚えることが重要なのではなく、eやlogは、文系の大学一年生が学ぶ科目の10ページ目ぐらいに当たり前のように出てくるので、まずはこの二つを必ず覚える必要がある、ということです。

そしてlog。
logはさすがに知っているよ！という方もいると思います。そう、logは文系でも習いますよね。こういうやつです。

なんですが、ここでいうlogは性質が違います。
文系の方が習うlogは、底が書かれていますよね。今扱っているlogには、底が書かれていません。
実際に底がないわけではないんですが、ものすごくよく使うので省略されているのです。

実際の底は先ほど扱ったeで、このようなeを底とした対数(log)のことを自然対数といいます。

e, logの微分

さて、eやlogがなんで基礎なのかはその微分を見ると非常にわかりやすいです。
まず、下式のようなeのx乗という関数を考えます。これをxについて微分するとどうなるでしょう？

正解は、そのままeのx乗になる、でした。めちゃくちゃ簡単でしょ？微分しても変わらないんです。
しっかり覚えてくださいね。eのx乗は、xについて微分しても形が変わりません。

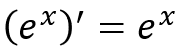
そしてなんとなく、あんな小難しい定義のめちゃくちゃ長い小数がなぜ重要で、わざわざeという文字で置かれているかが分かったのではないでしょうか。

(コラム：難しければ読み飛ばしてください)

この微分しても形が変わらないというのは非常に重要です。世の中には色々な式が存在しています。例えば物理なら運動方程式やマクスウェル方程式、統計ならベイズの定理など、いろいろあります。
そして例えば研究やゼミでは、未知の現象の説明が求められるわけですが、その際に自分で式を作って、それに当てはまっているか検証したりします。

そんな風な、実世界の現象を式にあてはめると、微分方程式と呼ばれるものが頻出します。eの関数は、最も簡単な微分方程式の解です。

例えば以下の微分方程式を考えます。

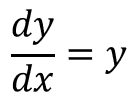
おそらく世界で最も簡単な形の微分方程式です。
この問題の意味は、yをxで微分したらyになりました。yはどんな関数ですか？という意味になります。つまりは微分しても形が変わらない、つまり答えはeのx乗になりますよね。
正確には、一般性を持たせて次の関数が解答となります。

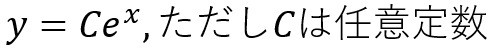
関数の前についている定数は微分には関係しませんから、これも微分しても形が変わらない関数ですよね。
このような非常に基本的な微分方程式で出てくるぐらい重要なんです。

(コラム終わり：ここから先は絶対に読んでください)

さて、eについての微分を考えたので、logについても考えます。次のような関数を考えます。

これを微分するとどうなるでしょう？

なんと、1/xになります。これまたきれいですね。
logという扱いづらそうで邪魔な奴が、微分したら綺麗に取れるんです。
後で扱う対数微分は、これを応用したものになります。

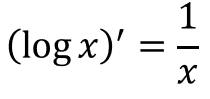
また、logxを微分したら1/xになるわけですから、その逆、つまり1/xを積分したらlogxになります。これも非常に基礎的なので絶対に覚えておきましょう。
正確に書くとこうなります。

logの真数は負の値を取れないので、絶対値を付けることを忘れないで下さい。

このように、微分や積分で素晴らしい破壊力を見せるeとlog。この二つが超重要な理由が少しは分かったのではないでしょうか。

さて、eのx乗およびlogの微分を覚えたところで、他の有名な関数の微分を覚えてしまいましょう。
もちろん教科書には証明が書いてあると思いますが、ここではそんなもの求められていないと思うので省略します。とにかく覚えてしまいましょう。

多項式関数の微分

文系の方は以下の形の関数の微分のみを習っているはずです。

xの2乗を微分すると2xになるあれです。
実際は、nは自然数じゃなくても成り立ちます。たとえば以下の関数を微分するとします。

√というのは1/2乗に等しいので、こういう風に書き換えられます。

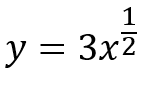
あとは普通に2乗の時とかと同様、指数を前に持ってきて、1引いてください。そうすると、

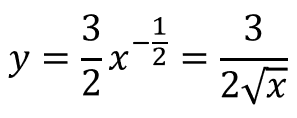
となります。

三角関数の微分

高校の時に習う三角関数にいやな思い出を抱いている方も多いかもしれません。
ですが、三角関数の微分はかなり簡単なので確実に覚えましょう。
以下の通りです。

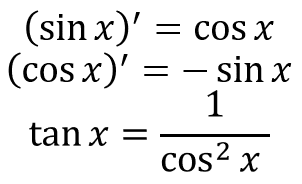
特にsinとcosは覚えやすいです。なんなら加法定理より簡単です。
特にすごいのが、sinxを微分したらcosx、それを微分したら-sinx、それを微分したら-cosx、それを微分したらsinxになるので、4回微分すると一周します。

tanxの微分は忘れやすいので気を付けてください。

対数微分

次のような関数の微分を考えます。

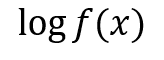
このlogはもちろんさっき教えた自然対数です。

f(x)はxのみで構成される関数ならなんでもいいです。x^2とか、sinxとか、√xとか。

それを微分すると、なんとこうなります。

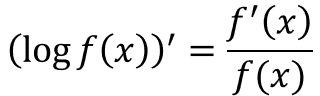
ものすごくきれいですね。

さっき、(logx)' = 1/xを教えましたが、あれもxを微分したら1なので、見事に当てはまっていますね。
ほかにも、例えばlog(sinx)の微分なら、答えはcosx/sinx = 1/tanxになります。

そしてこれを応用したのが対数微分法です。これを使うと、複雑な関数の微分ができることがあります。
次の関数の微分を考えましょう。

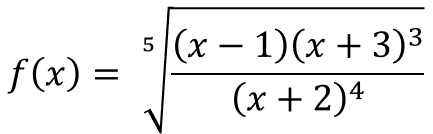
見るからに面倒ですね。しかし対数微分法を使うと、比較的マシに解けるんです。
というのも、左辺の対数を取るとf'(x)/f(x)で、右辺は1/5乗や積および商を分解できるので、複雑な形を崩すことができます。

ということでまず両辺の対数を取ります。

どうしてこうなるかが分からない人はまず対数を復習してくださいね。累乗は前に出て、積は和、商は差になりますね。

そしてこの両辺を微分します。ここでこの式を思い出しましょう。

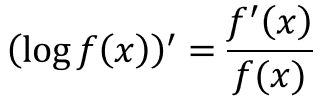
左辺の微分はこの式そのもので、右辺も一つ一つの項が対数関数なので、これに従えばすべて微分できます。
よって、

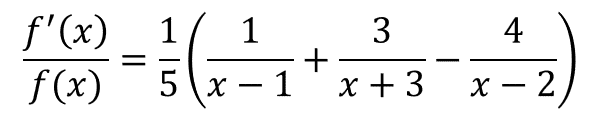
こうなります。両辺にf(x)をかけて、整理すると答えは

これが答えです。このように、対数関数の微分形式を利用して複雑な関数を対数を取ることで微分することを対数微分法といいます。

合成関数の微分

もうおなかいっぱいかもしれませんが、この合成関数の微分をやらないと絶対にダメです。
この項で終わりなので頑張りましょう。

なぜダメかというと、例えば今sinxの微分はできるわけですが、sin3xはどうでしょうか？
cos3xじゃないのって？違います。
そう、合成関数の微分を知らないと解けないんです。

合成関数の微分は、こんな風になります。

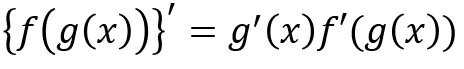
このままでは意味不明だと思うので解説します。

さきほどのsin3xという関数を思い出してください。
この関数って、f(x) = sinx、g(x) = 3x としたら、f(g(x))って書けますよね。
つまりは、sinxという関数の中に、3xという別の関数を合成させた形になっています。

この式の差す意味は、sin3xを微分したらcos3xっぽく見えるんですが、それにさらに3xを微分した結果を掛け合わせる必要があるということです。

つまり答えは3cos3xとなります。

ちょっとまだわかりにくいので、いくつか例を紹介します。

(1)　log(2x)

これも1/2xになりそうですが、それに2xを微分した結果をかける必要があります。つまり答えは2/2x=1/xです。

(2)　eの4x乗

同様に、e^4xに4xを微分したもの、つまり4をかけて、4e^4xが答えです。

もう少し難しいので行きましょう。

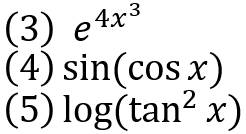
(3)、これはeのx乗の微分はそのままなので、eの4x^3乗に、4x^3を微分したものをかける必要があります。式にすると

となります。

(4)、sinxは微分するとcosxです。それに、中身のcosxを微分したものを掛け合わせます。式にすると

となります。

(5)、これはちょっと難しいですね。logxは微分すると1/xでした。それに、中身のtanxの二乗をかける必要があります。

しかしtanxの二乗も微分できません。こいつも合成関数です。
f(x) = x^2、g(x) = tanxとすればtanxの二乗というのはf(x)にg(x)を合成させたものだとわかると思います。f(x)を微分したものは2xなので、2tanxに中身のtanxを微分したものをかける必要があります。

まとめるとこうなります。

このように、一見難しい微分も、落ち着いてこの記事の知識を使えば解くことができます。

(最後はどの形で答えてもいいんですが、tanx = sinx/cosx と sin2x = 2sinxcosxを使ってきれいにできることも一応可能、という補足です)

まとめ

いかがだったでしょうか。
この記事に載っているのはマジの基礎なので、必ず抑えるようにしましょう。
eとlogの存在はもちろん、有名関数の微分も覚えて当然と言えます。

厄介なのが、この辺のことは覚えていないとどうしようもないということです。
もちろん証明できたりするんですけど、数学が苦手な文系の人には厳しいと思います。

さて、今回のことで結構大変な微分も行うことができたので、無敵！と思っている人、甘いです。
今回扱ったのは超基礎です。ここを当たり前のように使えるようにして、残りの勉強を頑張ってください。