【解答速報】北大理系数学2024第1問

問題

点$${t}$$を実数とし，$${xy}$$平面上の点$${{\rm P}(\cos2t, \cos t)}$$および点$${{\rm Q}(\sin t,\sin2t)}$$を考える。

(1) 点$${{\rm P}}$$と点$${{\rm Q}}$$が一致するような$${t}$$の値をすべて求めよ。
(2) $${t}$$が$${0 < t < 2\pi}$$の範囲で変化するとき，点$${{\rm P}}$$の軌跡を$${xy}$$平面上に図示せよ。ただし，$${x}$$軸，$${y}$$軸との共有点がある場合は，それらの座標を求め，図中に記せ。

解説

(1)

点$${{\rm P, Q}}$$が一致する、すなわち

$$
\begin{cases}
\cos2t &= \sin t\\
\cos t &= \sin2t
\end{cases}
$$

を満たす$${t}$$をすべて求める問題です。範囲の制限がないことに注意が必要です。上式はそれぞれ

$$
\begin{cases}
(2\sin t - 1)(\sin t + 1) &= 0 \\
\cos t(1-2\sin t) &= 0
\end{cases}
$$

と変形できます。これを満たすための必要十分条件は、

$$
\begin{cases}
\sin t &= -1, \cfrac{1}{2}\\
\sin t&= \cfrac{1}{2} \ または\ \cos t = 0
\end{cases}
$$

すなわち

$$
\sin t = -1, \frac{1}{2}\\
$$

である。したがって、求める$${t}$$の値は

$$
t = \bm{\frac{\pi}{6} + 2n\pi, \frac{5\pi}{6} + 2n\pi, \frac{3\pi}{2} + 2n\pi\ (nはすべての整数)}
$$

となる。

(2)

媒介変数表示された点$${{\rm P}(\cos2t, \cos t)}$$の軌跡を図示する問題です。まず、増減表は以下のようになります（微分するまでもないので変化の方向のみ）。

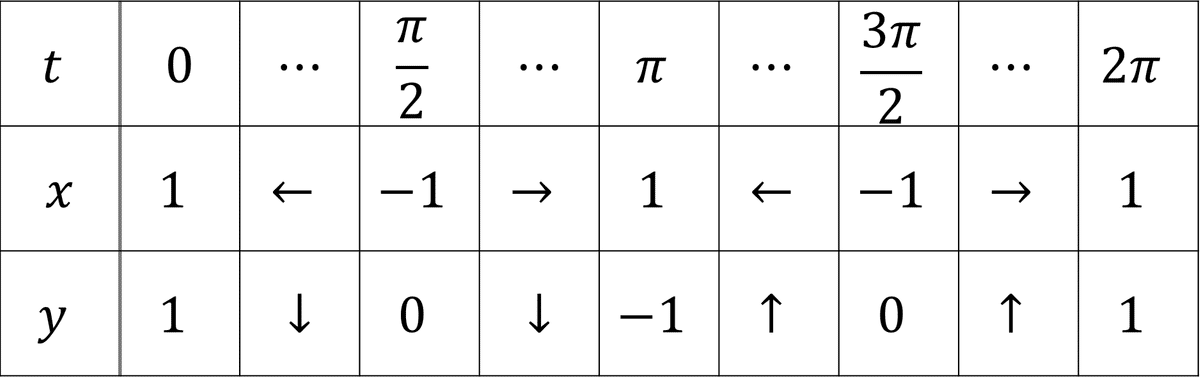
おおざっぱには$${(1,1)\to(-1,0)\to(1,-1)}$$と辿り、そこから来た道を戻るという感じです。このとき、往復では全く同じ経路をたどるはずです。なぜなら

$$
\begin{array}{lll}
\cos2t &= \cos2(2\pi-t)\\
\cos t &= \cos(2\pi-t)
\end{array}
$$

だからです。また$${x, y}$$軸と交わるのは、$${t = \pi/4, \pi/2, 3\pi/4,  \pi, 5\pi/4, 3\pi/2, 7\pi/4}$$のときで、重複は除くと共有点は$${(0,\pm1/\sqrt{2}), (-1, 0)}$$の3点です。以上を踏まえると、点$${\rm P}$$の軌跡は下の図のようになります。