
分数の割り算の謎解き:なぜひっくり返すの?
1 はじめに
皆さんにお尋ねです。分数を学習した小学生の子どもから、こんな質問をされたらどのように答えられますか?
今日学校でね、分数同士の割り算の計算を習ったんだ!!例えば、
$${\frac{13}{10}÷\frac{8}{5}}$$
だったら、
$${ \frac{13}{10}×\frac{5}{8}}$$
のように、÷を×にして÷の後ろの分数の分母と分子をひっくり返せばいいつて習ったんだ。
でもなんでひっくり返せばいいのか分からないから教えて!
こう聞かれてすぐに答えられる方は、かなりの数学力があると思います。「たしかに。なぜだろう?」が多いと思います。私もこっちです笑
この記事では、「なぜひっくり返すのか」について、2つの方法で説明していきます!
もしよければ、最後まで読んでください!!
2 具体例で説明!
具体的な例を使って「ひっくり返す」理由を説明します。
1km動くのに$${\frac{8}{5}}$$時間の充電が必要な電気自動車があります。実用的ではないですが、例なのでご勘弁を(;・∀・)

では、1時間充電するとどれだけ走れますか?$${\frac{5}{8}}$$kmですね。
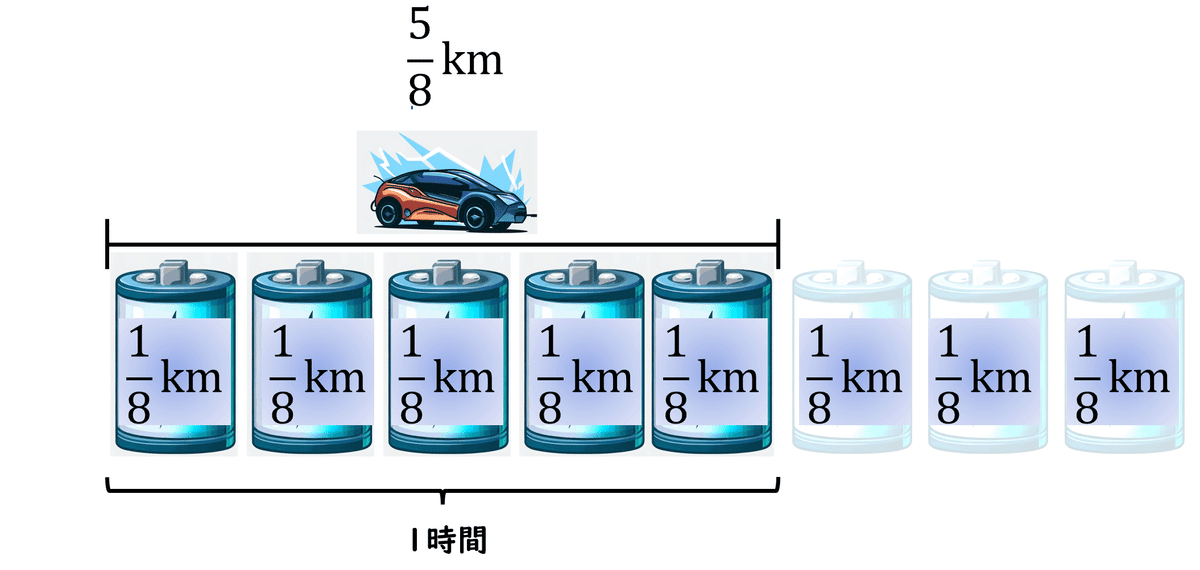
では、$${ \frac{13}{10}}$$時間充電すると、この車は何km走れますか?
それは、$${ \frac{13}{10}}$$の中に$${ \frac{8}{5}}$$がいくつ入るかと同じ意味だから、$${\frac{13}{10}÷\frac{8}{5}}$$・・・① で求められます。
でも、こう考えてもいいですよね?
1時間充電したら、$${\frac{5}{8}}$$km走る。
$${ \frac{13}{10}}$$時間充電すれば、$${\frac{5}{8}}$$を$${ \frac{13}{10}}$$倍した距離を走る。
つまり、$${\frac{13}{10}×\frac{8}{5}}$$・・・② の計算をすればいい。
①と②の結果は一致しないとおかしいから、
$${\frac{13}{10}÷\frac{8}{5}= \frac{13}{10}×\frac{5}{8}}$$
といえる。このような考えのもとで計算をしているので、分母と分子がひっくり返るのです!!
3 方程式で説明!
方程式というと、拒否反応を示されるかもしれませんが、必要な知識だけもう一度ここに書くので、まだこの記事を離れないで!!( ;∀;)
小学生に説明する場合は、$${x}$$を□に置き換えてあげてください。
では、説明する上で必要な知識は次の2つです。
・ 必要知識1 方程式では、両辺に同じ数をかけてもよい。
方程式は左辺と右辺が「=」で結ばれた式です。「=」で結ばれているということは、左辺と右辺が等しいということになります。等しい左辺と右辺に同じ数をかけても等しい関係は変わりません。
このことを式で書くとこうなります。
$${A=B}$$ならば、$${A×C=B×C}$$
具体例を示すと、
$${\frac{1}{2}x=3}$$
左辺と右辺に2をかける
$${\frac{1}{2}x×2=3×2}$$
このように、両辺に2をかけても「=」の関係は壊れません。
・ 必要知識2
ある数(x)を好きな数で割ったあとに、その好きな数をかけるとある数になる
これは具体的な例で説明します。
ある数を「5」とします。
これを好きな数(例えば3)で割り、その後に好きな数をかけると、
$${5÷3×3=5}$$ で、元のある数「5」に戻ります。
・ 方程式を使って「ひっくり返す」理由を説明します。
$${\frac{13}{10}÷\frac{8}{5}}$$の答えを$${x}$$とします。この場合、分数÷分数の計算の仕方が分からないから、答えを$${x}$$とするのです。
そしたら、次の式ができます。
$${\frac{13}{10}÷\frac{8}{5}=x}$$ ・・・①
両辺に$${\frac{8}{5}}$$をかけます
$${\frac{13}{10}÷\frac{8}{5}×\frac{8}{5}=x×\frac{8}{5}}$$
$${\frac{13}{10}=x×\frac{8}{5}}$$
$${x}$$の値が知りたいので、両辺に$${\frac{5}{8}}$$をかけます
$${\frac{13}{10}×\frac{5}{8}=x×\frac{8}{5}×\frac{5}{8}}$$
$${\frac{13}{10}×\frac{5}{8}=x}$$ ・・・②
①と②の式を比べると、右辺の$${x}$$が等しいから左辺も等しいといえる。
よって、
$${\frac{13}{10}÷\frac{8}{5}=\frac{13}{10}×\frac{5}{8}}$$
これで、「ひっくり返す」理由を説明できました。
4 おわりに
上で説明した理由から、分数のわり算では分母と分子をひっくり返すと学習します。でも、ほとんどの方は「方法」は覚えているけど、「仕組み」は分からないんじゃないかなと思います。
それは、小学校の算数は、演繹的に定理を導いていく「論理力」ではなく間違えずに答えを出す「計算力」に力を入れているからです。だから先生たちは、「方法」を覚えさせてひたすらドリルをさせていくのです。ですが、中学校以降の学習では、少しずつ「計算力」より「論理力」が求められ始めます。これは中学校になって「算数はできたのに数学ができない」という原因の1つになってるんじゃないかなと私が考えています。
最初は「方法」の教え込みでもいいと思いますが、学習が進んで、もう一度「なぜひっくり返すの?」など問い直すと面白いんじゃないかなと思います。
最後まで読んでいただき、ありがとうございました!!(人''▽`)
