
GPT-4oに東大入試数学2024(理科)【第3問】を解かせた結果
1 GPT-4oに解かせた問題
今回解かせたのは、東京大学令和6(2024)年度第2次学力試験数学(理科)第3問です。

2 解かせた結果の概要
(1) 1回目 正解
(2) 1回目 正解
(3) 1回目 大学での学習内容を用いたため不正解
↓指摘後
2回目 不正解
↓指摘後
3回目 不正解
3 詳細
・(1)について
点Pが座標平面上で動く際の規則に基づいて、点Pがとりうる点の座標を考えてみます。最初に、点Pは点(2,1)にいます。その後、次の規則に従って動きます。
1. 確率1/3でx軸に関して対称な点:$${ (2, -1) }$$
2. 確率1/3でy軸に関して対称な点:$${ (-2, 1) }$$
3. 確率1/6で直線y=xに関して対称な点:$${ (1, 2) }$$
4. 確率1/6で直線y=-xに関して対称な点:$${ (-1, -2) }$$
これを元に、点Pがとりうる座標を求めてみましょう。
### 時刻t = 1
- 初期点:$${ (2, 1) }$$
- 1秒後に移動する点:
1. 確率1/3で $${ (2, -1) }$$
2. 確率1/3で $${ (-2, 1) }$$
3. 確率1/6で $${ (1, 2) }$$
4. 確率1/6で $${ (-1, -2) }$$
したがって、点Pがとりうる座標は以下の通りです。
$${ \{(2, -1), (-2, 1), (1, 2), (-1, -2)\} }$$
### 時刻t = 2
各々の座標に対して再び同じ規則を適用して、点Pがとりうる座標を求めます。
#### 点 $${ (2, -1) }$$ からの移動
1. 確率1/3で $${ (2, 1) }$$
2. 確率1/3で $${ (-2, -1) }$$
3. 確率1/6で $${ (-1, 2) }$$
4. 確率1/6で $${ (1, -2) }$$
#### 点 $${ (-2, 1) }$$ からの移動
1. 確率1/3で $${ (-2, -1) }$$
2. 確率1/3で $${ (2, 1) }$$
3. 確率1/6で $${ (1, -2) }$$
4. 確率1/6で $${ (-1, 2) }$$
#### 点 $${ (1, 2) }$$ からの移動
1. 確率1/3で $${ (1, -2) }$$
2. 確率1/3で $${ (-1, 2) }$$
3. 確率1/6で $${ (2, 1) }$$
4. 確率1/6で $${ (-2, -1) }$$
#### 点 $${ (-1, -2) }$$ からの移動
1. 確率1/3で $${ (-1, 2) }$$
2. 確率1/3で $${ (1, -2) }$$
3. 確率1/6で $${ (-2, -1) }$$
4. 確率1/6で $${ (2, 1) }$$
したがって、時刻t = 2における点Pがとりうる座標は以下の通りです。
$${ \{(2, 1), (-2, -1), (-1, 2), (1, -2)\} }$$
### 時刻t = 3
次に時刻t = 3での移動も同様に計算します。
上記の座標それぞれに対して再び規則を適用すると、点Pがとりうる座標は同じパターンを繰り返すため、点Pがとりうる全ての座標は次の8点です。
$${ \{(2, 1), (2, -1), (-2, 1), (-2, -1), (1, 2), (1, -2), (-1, 2), (-1, -2)\} }$$
これで、点Pがとりうる点の座標を全て求めました。
・(2)について
点Pが最初に点(2,1)にいるとき、n秒後に再び点(2,1)にいる確率と、n秒後に点(-2,-1)にいる確率が等しいことを示すためには、各ステップでの移動確率が対称であることを利用します。
### 状態遷移の確率
点Pが任意の点 $${(a, b)}$$ にいるとき、その1秒後に点Pがいる可能性のある4つの点とその確率は次の通りです:
1. 確率1/3で $${ (a, -b) }$$ (x軸に関して対称)
2. 確率1/3で $${ (-a, b) }$$ (y軸に関して対称)
3. 確率1/6で $${ (b, a) }$$ (直線 $${ y = x }$$ に関して対称)
4. 確率1/6で $${ (-b, -a) }$$ (直線 $${ y = -x }$$ に関して対称)
これらの遷移確率は対称的であり、各ステップでの対称性を保持します。
### 対称性の観察
点Pが点(2,1)にいるとき、各ステップで以下の対称的な状態が成り立ちます:
1. 点(2,1) と 点(-2,-1)
2. 点(2,-1) と 点(-2,1)
3. 点(1,2) と 点(-1,-2)
4. 点(1,-2) と 点(-1,2)
この対称性はn秒後にも維持されるため、任意の時刻において対称的な点の確率が等しくなります。
### 証明の概要
1. $${ t = 0 }$$ 秒後、点Pは点(2,1)に確率1でいる。
2. $${ t = 1 }$$ 秒後、点Pは4つの点 $${(2, -1), (-2, 1), (1, 2), (-1, -2)}$$ のいずれかにいる確率がそれぞれ定まる。これらの点は点(2,1)と点(-2,-1)に対して対称的な点を含む。
3. このプロセスを繰り返すと、各時刻において点Pの位置の確率分布は対称性を維持します。
したがって、n秒後に点Pが点(2,1)にいる確率と、n秒後に点Pが点(-2,-1)にいる確率は等しいことが示されました。
以上により、対称性に基づく状態遷移の確率の観察から、点Pが点(2,1)にいる確率と、点(-2,-1)にいる確率が等しいことが示されます。
おおよそ考え方が正しいので、正解としました。
・(3)について
点 $${ P }$$ が最初に点 $${ (2, 1) }$$ にいるとき、n秒後に再び点 $${ (2, 1) }$$ にいる確率を求めるために、状態遷移の確率を考えます。これはマルコフ連鎖の問題として扱うことができます。
### 状態遷移行列の構築
考えられる状態は以下の8点です:
$${ \{ (2,1), (2,-1), (-2,1), (-2,-1), (1,2), (1,-2), (-1,2), (-1,-2) \} }$$
これらの点間の遷移確率を行列形式で表します。
#### 状態遷移行列 $${ P }$$
各点から他の点への遷移確率を求め、8×8の行列 $${ P }$$ を作成します。
状態の順序は上記の順とし、行列の各要素 $${ P_{ij} }$$ は、状態 $${ i }$$ から状態 $${ j }$$ への遷移確率を表します。
- $${ P_{11} }$$: (2, 1) → (2, 1)
- $${ P_{12} }$$: (2, 1) → (2, -1)
- $${ P_{13} }$$: (2, 1) → (-2, 1)
- $${ P_{14} }$$: (2, 1) → (-2, -1)
- など
具体的な遷移確率は対称性から次のようになります:
$${P = \begin{bmatrix}1/3 & 1/3 & 1/3 & 0 & 1/6 & 1/6 & 0 & 0 \\1/3 & 1/3 & 0 & 1/3 & 1/6 & 0 & 1/6 & 0 \\1/3 & 0 & 1/3 & 1/3 & 0 & 1/6 & 0 & 1/6 \\0 & 1/3 & 1/3 & 1/3 & 0 & 0 & 1/6 & 1/6 \\1/6 & 1/6 & 0 & 0 & 1/3 & 1/3 & 1/3 & 0 \\1/6 & 0 & 1/6 & 0 & 1/3 & 1/3 & 0 & 1/3 \\0 & 1/6 & 0 & 1/6 & 1/3 & 0 & 1/3 & 1/3 \\0 & 0 & 1/6 & 1/6 & 0 & 1/3 & 1/3 & 1/3 \\\end{bmatrix}}$$
### 初期状態ベクトル
初期状態では、点 $${ (2,1) }$$ にいる確率が1なので、初期状態ベクトル $${ v_0 }$$ は次のようになります:
$${ v_0 = [1, 0, 0, 0, 0, 0, 0, 0] }$$
### n秒後の確率
n秒後の状態ベクトル $${ v_n }$$ は以下のように求められます:
$${ v_n = v_0 \cdot P^n }$$
ここで、 $${ P^n }$$ は遷移行列 $${ P }$$ をn乗した行列です。最初の要素 $${ (2,1) }$$ にいる確率を求めるためには、行列 $${ P^n }$$ の第1列の第1行の要素を求めます。
### 計算
行列計算を行い、n秒後の確率を求めます。具体的な計算はPythonなどのツールを使用すると便利です。
```python
import numpy as np
# 状態遷移行列
P = np.array([
[1/3, 1/3, 1/3, 0, 1/6, 1/6, 0, 0],
[1/3, 1/3, 0, 1/3, 1/6, 0, 1/6, 0],
[1/3, 0, 1/3, 1/3, 0, 1/6, 0, 1/6],
[0, 1/3, 1/3, 1/3, 0, 0, 1/6, 1/6],
[1/6, 1/6, 0, 0, 1/3, 1/3, 1/3, 0],
[1/6, 0, 1/6, 0, 1/3, 1/3, 0, 1/3],
[0, 1/6, 0, 1/6, 1/3, 0, 1/3, 1/3],
[0, 0, 1/6, 1/6, 0, 1/3, 1/3, 1/3]
])
# 初期状態ベクトル
v0 = np.array([1, 0, 0, 0, 0, 0, 0, 0])
# n秒後の確率ベクトルを計算
n = 10 # 例えば10秒後
vn = np.linalg.matrix_power(P, n) @ v0
# 点(2,1)にいる確率
prob_2_1 = vn[0]
prob_2_1
```
これにより、n秒後に点(2,1)にいる確率が求められます。具体的な数値はnに依存しますが、一般的にはこの手法を用いて計算することができます。
行列を使って回答しているので、数列を使って考えるように指摘しました。
数列を用いて説明する方法を考えてみましょう。まず、点 $${ P }$$ が最初に点 $${ (2, 1) }$$ にいるとき、n秒後に再び点 $${ (2, 1) }$$ にいる確率を求めます。この問題を解くために、次の確率の数列を定義します。
- $${ a_n }$$ : n秒後に点 $${ (2, 1) }$$ にいる確率
- $${ b_n }$$ : n秒後に点 $${ (2, -1) }$$ にいる確率
- $${ c_n }$$ : n秒後に点 $${ (-2, 1) }$$ にいる確率
- $${ d_n }$$ : n秒後に点 $${ (-2, -1) }$$ にいる確率
- $${ e_n }$$ : n秒後に点 $${ (1, 2) }$$ にいる確率
- $${ f_n }$$ : n秒後に点 $${ (1, -2) }$$ にいる確率
- $${ g_n }$$ : n秒後に点 $${ (-1, 2) }$$ にいる確率
- $${ h_n }$$ : n秒後に点 $${ (-1, -2) }$$ にいる確率
初期条件は次のようになります:
$${ a_0 = 1 }$$
$${ b_0 = c_0 = d_0 = e_0 = f_0 = g_0 = h_0 = 0 }$$
次に、n秒後の確率を計算するための遷移方程式を構築します。各点から他の点への遷移確率に基づいて次のようになります:
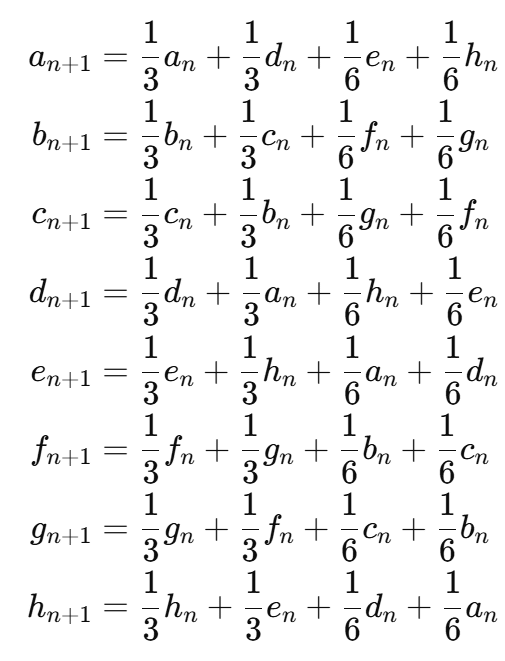
これらの方程式に基づいて、数列を再帰的に計算することができます。例えば、n=1のとき:

このようにして、再帰的に各ステップでの確率を計算することができます。一般のnについても同様に計算することで、n秒後に点 $${ (2,1) }$$ にいる確率 $${ a_n }$$ を求めることができます。
数列が8つ出てきましたが、問(2)で対称性に注目したので、数列は4つに減らせます。
なので、対称性に注目すればよいのでは?と指摘しました。
確かに、対称性に注目すると計算が簡単になります。対称性を利用して、n秒後に点 $${ (2, 1) }$$ にいる確率を求めることができます。
### 対称性の利用
次の8つの点を考えます:
$${ \{ (2,1), (2,-1), (-2,1), (-2,-1), (1,2), (1,-2), (-1,2), (-1,-2) \} }$$
対称性により、点 $${ (2, 1) }$$ と点 $${ (-2, -1) }$$ にいる確率は等しいことがわかります。また、その他の対称な点についても同様です。このため、以下の確率が等しいことがわかります:
$${ a_n = d_n }$$
$${ b_n = c_n }$$
$${ e_n = h_n }$$
$${ f_n = g_n }$$
これを利用して、簡略化した方程式を立てることができます。
### 確率の簡略化
以下のように新しい確率を定義します:
$${ x_n = a_n = d_n }$$
$${ y_n = b_n = c_n }$$
$${ z_n = e_n = h_n }$$
$${ w_n = f_n = g_n }$$
この新しい確率を使って遷移方程式を簡略化します:

### 初期条件初期状態では、点 $${ (2,1) }$$ にいる確率が1なので:$${ x_0 = 1 }$$$${ y_0 = z_0 = w_0 = 0 }$$### 再帰方程式の解この再帰方程式を解くと、n秒後の各点にいる確率がわかります。例えば、初めの数ステップを計算してみましょう。

次のステップも同様に計算できます。

このプロセスをnステップ繰り返すことで、n秒後の各点にいる確率が求められます。特に、n秒後に点 $${ (2,1) }$$ にいる確率 $${ x_n }$$ を計算することができます。再帰方程式を解くことで、任意のnについての一般的な解が得られます。初期条件と再帰方程式に基づいて、Pythonや他のプログラムを使用して具体的な数値を計算することも可能です。このように対称性を利用することで、問題を簡略化して解くことができました。
さこの回答でもそうですが、n秒後の確率についてはPythonなどのプログラムを動かして解く、と言っているため、GPT-4oとしてはこの回答が限界のようです。
4 評価
今回は、2問正解できました。
(1)では、無限に答えが存在するように思える問題を、状態遷移を1つ1つ考えて解き、そのパターンを調べ上げることができました。
(2)では、状態遷移の対称性に着目して、証明できました。この数学的な考え方に行き着いているのは、流石だなと感心しました。
(3)では、実際にPythonのプログラムを動かしましたが、ちゃんと最後まで動きませんでした。
おそらくどこかしらが間違っているのだと思います。
最後まで読んでいただき、ありがとうございました。

この記事が気に入ったらサポートをしてみませんか?
