【京都大学1974年度入試数学(理系)第1問】美しい解法

今月も京都大学の古い問題を取り上げたいと思います。1974年度入試数学(理系)の第1問です。生まれていない方も多そう。(^^;;

京都大学　百周年時計台記念館
2015年5月5日、Soraie8288撮影、Wikipediaより

[問題] 0 ≦ α < β < γ < 2π であって
　　　　cos α + cos β + cos γ = 0，sin α + sin β + sin γ = 0
であるという．β - α と γ - β の値を求めよ．

見ての通り、問題そのものは難しくないです。まずは解答を書いてみたいと思います。

[解答] sin^2 γ + cos^2 γ = 1 より (sin α + sin β)^2 + (cos α + cos β)^2 = 2 + 2(cos α cos β + sin α sin β) = 2 + 2 cos (β - α) = 1 であるので，

cos (β - α) = - (1/2)

である．0 ≦ α < β < 2π から 0 < β - α < 2π であるので，β - α = 2π/3 もしくは 4π / 3 が得られる．

一方，sin^2 α + cos^2 α = 1 より (sin β + sin γ)^2 + (cos β + cos γ)^2 = 2 + 2 cos (γ - β) =1 であるので，

cos (γ - β) = - (1/2)

である．0 < β < γ < 2π から 0 < γ - β < 2π であるので，γ - β = 2π/3 もしくは 4π / 3 が得られる．

ここで，(β - α) + (γ - β) = γ - α であるが、0 ≦ α < γ < 2π から 0 < γ - α < 2π であり、この条件を満たすのは β - α = γ - β = 2π/3 のときのみである．

逆にこのとき、0 ≦ α < 2π/3 であれば問題の全ての条件を満たすことが簡単に確認できる。[解答終]

問題集の中で見かける解答はこのようなものが多いかと思います。また、多くの方もこのように解くと思います。

確かにこの解法は入試本番において実戦的ではあるけれども、正直なところ入試の立場ではない私にとってつまらない解法です。

問題の本質が見えないと思いませんか？

別解：視点を変えてみる

ということで、この問題を次のように表記してみます。

そう！これ、平面ベクトルの問題なんです。同じことですが、

と書いて複素平面を思い浮かべてもいいでしょう。

この問題、原点から異なる方向に出ている長さ 1 の 3 本のベクトルの和が零ベクトルとなるとき、3本のベクトルの方向がどうなっているかを聞いているのです。

そう言われたら、おそらく誰もが「正三角形の重心から頂点！」となるはずです。だから、答えが 2π/3 すなわち 120° になることは計算しなくても分かります。

最初にあげた解答より、こちらの思考に沿って示す方が私には美しく感じます。ベクトルで表記しただけで問題に図形的な意味を与え、しかも答えまでもが導かれている。

芸術を説明するのが難しいように、数学の中の美を説明するのは難しいですが、上記のような話を聞いて楽しさとか美しさを見出せる感覚は数学が超得意な人に特有です。

証明を読んで「美しい」「美しくない」と発言できるようになったら一人前と言っていいでしょう。笑

さて、先ほどの話に戻りますが、答えが 2π/3 しかないことを論証しなければいけないので、真面目に解答を作らないといけないのですが、上記の視点を持つと答え方はいろいろと出てくるはずです。

[別解] 例えば、最初の2つのベクトルを合成するならば次の式が得られます。

(ここで α = (α+β)/2 + (α-β)/2 かつ β = (α+β)/2 - (α-β)/2 に注意)

要は角度 α と β のベクトルの和を取ると (α + β)/2 の角度を持つベクトルになると言っています。そりゃそうだ。

ただし、|α - β| の値によってどちら向きになるか、大きさがどうなるかが変わるとも言っています。特に、|α - β| > π (=180°) のときには、角度 (α+β)/2 の方向とは逆になると言っています。当然。下の図で確認してください。

(π < |β - α| <2π のとき、角度 (α+β)/2 の方向は緑になります。)

以下、計算を続けましょう。sin^2 γ + cos^2 γ = 1 より

が得られ、0< β - α < 2π より β - α = 2π/3 もしくは 4π/3 となります。

β - α = 2π/3 のとき、

が得られ (n は整数)、0 ≦ α < β < γ < 2π を満たすためには n = 0 であり、逆に n = 0 のときには γ = π + (α + β)/2 から γ - β = π - (β - α)/2 = 2π/3 が得られ、0 ≦ α < 2π/3 であるときに条件を満たします。

(注) n < 0 のときには γ = -π + (α+β)/2 < β となり、n > 0 のときには γ > 3π となるので、n = 0 に限定される。

β - α = 4π/3 のとき、

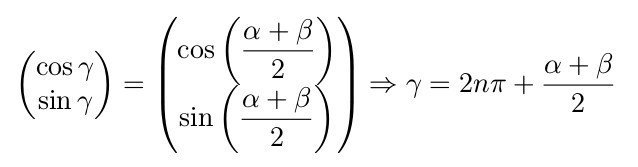
が得られる (n は整数) が、n ≦ 0 のとき γ ≦ (α + β)/2 < β となり、n > 0 のとき γ > 2π となるため解なしとなります。[別解終]

美しい解法とは？

この解法だと同じ式変形でもベクトルという意味を持って行われており、最終的に 3つのベクトルの位置関係まで求まります。

答えは当然同じになりますが、その過程で得られる情報であったり、解法の見通しのよさには雲泥の差があります。

特に、前者の解法では答えが 2π/3 である必然性が見えない一方、後者では最初から正三角形の頂点と重心の関係を意識していて 2π/3 になることが前提になっています。

解法の美しさは主観だとしても、情報量の観点でどちらを「いい解法」と呼ぶかは一目瞭然です。

また、主観である美しさについてはいくつかの観点がありますが、私は見通しのよさはその一つだと思っています。

前者はやみくもに計算している印象を受けますが、後者は何をしているかが明確で式変形に意図がある。その点で言っても後者の解法は「いい解法」だと思います。

さらには、後者の解法は次の問題の解法に拡張することも可能です。

[問題] 0 ≦ α < β < γ < δ < 2π であって
　　cos α + cos β + cos γ + cos δ = 0，sin α + sin β + sin γ + sin δ = 0
であるという．γ - β と δ - γ を β - α を用いて表せ．

この問題を後者の解法と同じように解くと δ - γ = β - α かつ (γ + δ)/2 = (α + β)/2 + π から (δ - γ)/2 = (α + β)/2 - γ + π = π - (β - α)/2 - (γ - β) すなわち γ - β = π - (β - α)/2 - (δ - γ)/2 = π - (β - α) が得られます。 

この答えから、γ = α + π と δ = β + π が得られるので、長方形の対角線の交点と4頂点の関係が出てきます。(この答えも予想がつきますよね)

このように、解法の適用範囲の広さも「いい解法」や「解法の美しさ」の条件の一つです。

見ていただいた通り、同じ問題の解法や証明でも、美しかったり美しくなかったりしますので、できるなら解法や証明の「美しさ」にこだわってみてはいかがでしょうか？

この「美しい」「エレガント」については、その逆の「汚い」「醜い」とともにいずれ何かの機会に書こうか思います。

(注) 解法は答えを導く議論の流れ(そこに横たわる思考)、解答は解法に基づいて書かれた答えそのものを意味します。今回美しさやエレガントさを議論しているのは解法についてです。ちなみに、日本評論社『数学セミナー』の人気コーナー「エレガントな解答をもとむ」は、私の定義にしたがえば「エレガントな解法による解答」を募集しています。

蛇足

最後に、同じ問題でベクトルが5本以上になった場合はどうなるでしょうか？

実は解のバリエーションが増えてしまうため、簡単には記述できなくなります。

例えば、ベクトルが5本の場合、もちろん正5角形の重心から各頂点へのベクトルになっている場合に条件を満たしますが、5本のベクトルを2本と3本に分けて、2本は互いに正反対の向き、残りの3本は重心から正三角形の頂点の向きになっている場合、条件を満たします。

ベクトルが6本の場合も、3組のベクトルの対に分けて、それぞれが正反対の方向になっているときに条件を満たしますが、3本のベクトルからなる2つのグループに分けて、それぞれが重心から正三角形の頂点の向きになっている場合にも条件を満たします。

このように、ベクトルが5本以上になった場合にはいろいろな組み合わせが考えられるため、今回の解法が適用できるのは4本までが限界であることがわかるかと思います。