色を科学する　その⑪ 均等色空間と色差＜中編＞ 「log」や「べき」で明るさを表す

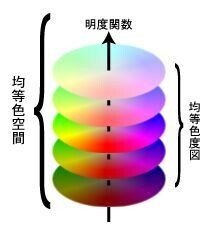
　＜前編＞で均等色度図のことを書きました。均等色度図はその名の通り、色相と彩度のみの情報を持ち、明るさの情報がありません。そこにヒトの感覚に合致する明るさ尺度（モノサシ）である「明度関数」を組み合わせることにより、均等色空間が完成し、その空間での距離が色差となります。

　※本コンテンツは有料となっていますが、無料で最後まで読めます。共感いただける方はサポートよろしくお願いします。

輝度以外のモノサシが必要

　明るさのモノサシの一つである輝度(や物体色のY)が有効なのは、同じ明るさか？ or せいぜい明るさが近いか/遠いか？くらいの判断です。その色がどのくらい明るく感じるか？ or 2色がどのくらい明るさの違いがあるか？は保証していません。

　また、「輝度・照度・明度・明るさ の違いを説明できますか？」でも書きましたが、物体色を輝度で表現しても感覚と合わず、あまり意味を持ちません。なので、完全拡散反射面(簡単にいうと白)を100とした相対化をして、cd/m^2の単位をなくします(「色を科学する　＜番外編＞ XYZを自分で計算してみよう！」を参照)。

　しかし、これだけだと不十分で、明るさの絶対量や明るさの差を表現するには、もうひと手間必要なのです。

　例えば、真っ暗で部屋で、明かりを一つ点けると非常に明るくなったと感じます。しかし、同じ明かりをもう一つ点けた時、明るさが2倍になった感はないですよね？1.3倍とか1.5倍になったくらい。光の量である光束は確実に2倍に、輝度(＝単位立体角＆単位面積当たりの光束)、も2倍になっているはずなのに。

　簡単にいうと、明るさ感は輝度に対して非線形で、輝度が2倍になったら、明るさ感が2倍になるとは限らない(そうなったら線形といえる)。輝度が絶対的に小さい領域ではその差に鋭敏になり、ある程度の光の量になると飽和して（サチって）頭打ちになるような特性なのです。例えば↓の図のように。

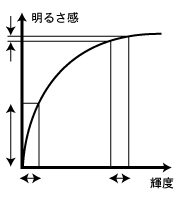
↑同じ輝度の差でも明るさ感の差が大きく異なる

　これは、ヒトの目が、0.0003lx(新月の夜)～100,000lx(直射日光下)という広いダイナミックレンジの中でうまく稼働するための工夫なのでしょう(もちろん、瞳孔の拡縮や桿体⇔錐体の変更も含まれますが）。

「log」と「べき」

　このような、入力(輝度)が小さいところでは鋭敏に反応し、大きくなるにつれ、鈍感になっていく特性は対数(log)や指数(べき乗)で表現できます。

　例えば、Weberの法則をもとに、Fechnerが唱えた「Weber-Fechnerの法則」では、知覚上の強度をP、刺激の強度をIとすると、下記のように表現できます。

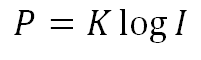
(Kは定数)

　また、Stevensが唱えた「Stevensのべき法則」では、下記のように表現できます。明るさ（色）の領域ではこのべき法則が当てはまりがよく、良く使われます。

　(Kは定数、nは刺激の種類に依存)

　そして、明るさに関しては、n=0.33であることが(マグニチュード推定法を用いた)実験によりわかっています。

　ちなみに、電気刺激だとn=3.5、nが正なので、中学で習う二次関数(y=x^2)と同じような形状になり、刺激が強くなると、痛みが指数関数的にどんどん増大する(！)ことになります。このあたり、実験心理学や知覚心理学で出てくる領域です。

　そして、「べき乗」ってことは、logをとると線形となり、直線的(比例)の関係になります。

実際の明度関数

CIE1964U*V*W*色空間の明度関数

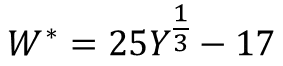
　n=1/3、つまり0.3333...となってます。

CIE1976L*a*b*およびL*u*v*色空間の明度関数

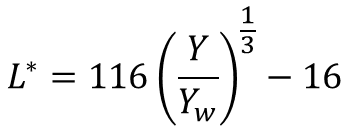
　n=1/3でW*と同じですが、Yを白のYであるYwで正規化しています。これは色順応を考慮しているためです(詳細は後述)。また、暗い色(Y/Yw<0.008856)の場合は、別の式を使います。

マンセル表色系の明度（Value）関数

　　突然長い式になりました。しかもV＝f(Y)の形ではなく、Y＝f(V)と、逆の形になっています。これは、もともとマンセル表色系が、数学的に構築されたのではなく、色票がベースになっているからです。

　マンセルが作った(均等になるように並べた)色票を、OSA(アメリカ光学会)が計測したところ、結果としてこのような5次式の関係性が見られた、そして、VをYの関数で表現することは数学的に複雑でできなかった、ということです。

　よって、YからVを求める際は、5次方程式となり、解の公式などはないので、特殊な方法(たとえば、Newton-Raphson法)を用いて解を求めます。

　ちなみに、一般に「マンセル表色系」と呼ばれているものは、OSAが色票の計測結果をもとに修正した(不自然な位置関係にある色を直すなど)、「修正マンセル表色系」を指します。修正前の「マンセル表色系」は基本的にもう使いません。

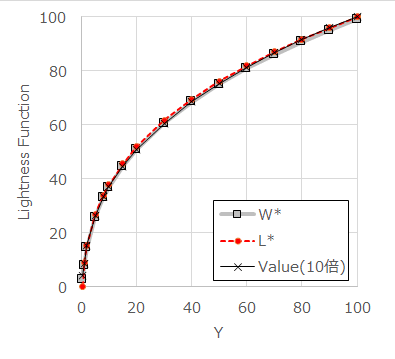
　W*、L*、Value(ただし、レンジを0-100にするため10倍したもの)を比較したグラフが↓です。ほとんど差はなく、1/3乗を用いたシンプルな関数により、マンセルValueを精度よく近似できていることがわかります。

　

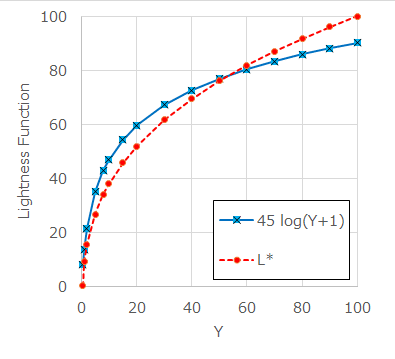
　また、logとべき乗も比較してみます。やや形状が異なりますが、近い特性を持っていることがわかります。

　ようやく、均等色度図と明度関数がそろいました。均等色空間と色差は＜後編＞で！