色を科学する　＜番外編＞ XYZを自分で計算してみよう！

　XYZを計算する∫やΣを使った数式、眺めていてもよくわからず、結局わからないまま…。そんなときは、自分で計算してみるのが一番だと思います。Excelを用いて1ステップずつ手順を説明しますので、やってみましょう！

⓪物体色のXYZ計算式のおさらい

　↓この式です（物体色の場合）。色関係の検定試験で出てきて、拒否反応が出る人が多いようです。

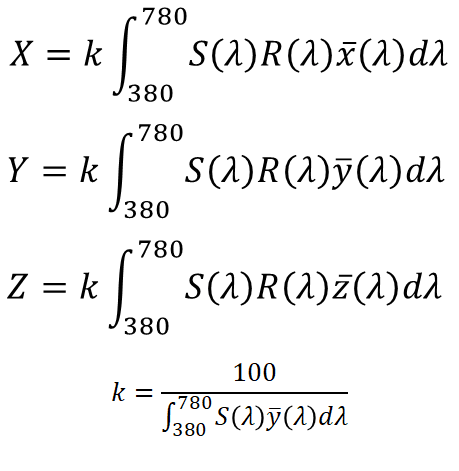
　S(λ)は光源の分光分布、R(λ)は物体の分光(立体角)反射率、x(λ)、y(λ)、z(λ)は等色関数です。光、物、眼の分光特性を掛けて、（波長で）積分し、最後に係数kを掛けるという手順です。

　ここでは、使用頻度の高い物体色を対象とし、シンプルにするために400-700nmの範囲で計算します（380-400、700-780は感度も低く、大勢には影響しないので）。計算にはExcelを用います。

①まずは、光、物、眼をそろえよう

　最初に「光」と「物」です。光として、CIEの補助標準イルミナントC（C光源）を採用し、物は肌(の色)とします。

　C光源は、555nmのエネルギーを1として正規化した相対エネルギー、肌は、完全拡散反射面の時すべての波長で1となるように正規化した反射率で表しています。

　C光源は北窓昼光なので、紫外線を含む単波長成分が多いですね。肌は、メラニン依存の全体に右上がりの特徴と、ヘモグロビンによる550nm付近の吸収が見られます。

　以前も書きましたが、物体色の計算をする場合は、明るさの絶対値情報は重要でなく、最終的に相対化されるので、実は正規化してても/してなくても問題ありません（後述）。光源色の場合は、明るさの絶対値が重要なので、単位も含めて厳密に設定します。

　次に、「眼」ということで、既出の等色関数です。

　これは何度も紹介してますね。

②「眼に入ってくる光」の計算

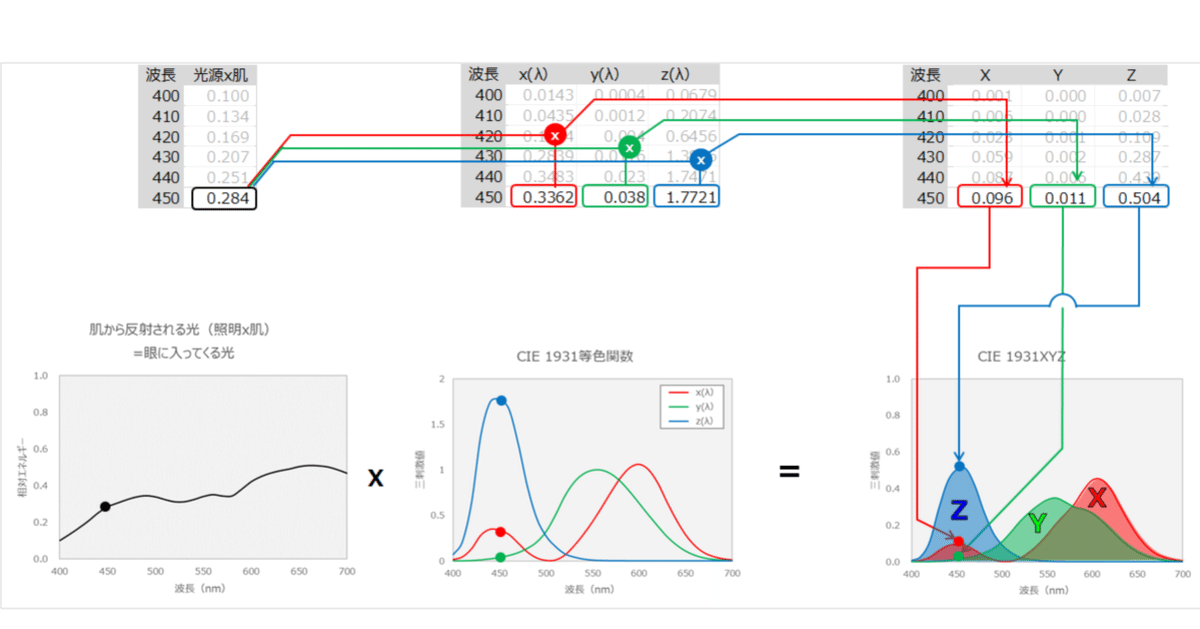
　XYZの計算では、光源の分光分布、または物体の分光反射率の個々がどうであるかは問題ではなく、「眼に入ってくる光」のみが重要で、この場合「肌から反射される光」がそれにあたります。よって、波長ごとに光源のエネルギーと物体の反射率を掛け合わせます。

　光源色の場合は、物は考えず、光源の分光エネルギーがそのまま「眼に入ってくる光」ですね。

　400nmの場合、C光源の相対エネルギーが0.633、肌の反射率が0.159なので、0.633*0.159＝0.100といった具合です。

　照明と物体の両方の特性を考慮したようなかたちになりました。

ここで、「眼に入ってくる光」のみが重要というのはXYZの場合に限りです。「The Dressの話」でも書いたように、ヒトの視覚には、色順応等の機能があり、照明光と物体の色は分けて処理されます。結果として、照明光をキャンセルし、物体の色を安定して知覚できるようになっています。よって、たとえば、CIE L*a*b*色空間では、眼に入ってくる光以外に、照明光（Xw,Yw,Zw）も入力します。

　「色を科学する　その⑦ XYZのトリセツ」でも書いたように、XYZ表色系は本来「暗闇での単色」が対象であり、その場合、色順応が起こらないので、眼に入ってくる光で色知覚が決定されます。

③波長別のXYZ三刺激値計算

　眼に入ってくる光が、x(λ)、y(λ)、z(λ)という感度を持つ3種の光受容細胞に吸収されたときの応答量＝三刺激値を、波長ごとに計算します。つまり、波長ごとに、光のエネルギーと感度を掛け合わせます。

　450nmの数値で説明すると↓こんな感じで、掛け算の結果も3つの値（その波長での三刺激値XYZ）

　もともと、等色関数は、等エネルギー（単位エネルギー）の単波長光に対する三刺激値だったので、任意の単色光に対しては、その比率を掛けることで三刺激値が算出できます。

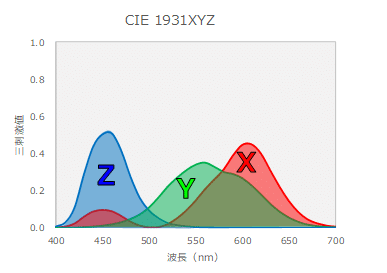
　これを全波長で行うと下図のような、各波長の三刺激値XYZを表現したグラフが完成します。

　↑この表やグラフはあくまで、各波長に対しての三刺激値であり、求めたいのは400-700nm全域の三刺激値です。そのためには、3つの曲線の面積を算出する必要があります。なので、積分記号である∫(インテグラル)が出てくるのです。

④実際には積分しません！

　　3つの曲線（の下の領域）の面積を求めるとき、実際には積分しません。細かい短冊状に切って、その長方形の面積を足し合わせます。下図は「色を科学する　その②」でも説明したものですが、今回はΔλ＝長方形の幅が10nmということになります。

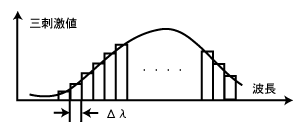
　長方形の幅をどんどん狭くしていくと、結局「積分」になるんですけどね。関数の形が、たとえば「ｙ＝ax^3+bx^2+cx+d」といったような、きれいな数式で表現できれば積分公式で面積を求められるのでいいのですが、まずそうならないので、近似解を求める手法(短冊状に切って面積を足す)を取ります

　この短冊状の長方形の面積は、

幅＊高さ＝10nm＊曲線のその波長での値

　となるので、ひとつ前の表の各値に10を掛け、それらを400-700nmで全部足し合わせれば（＝Σを取る）でます。

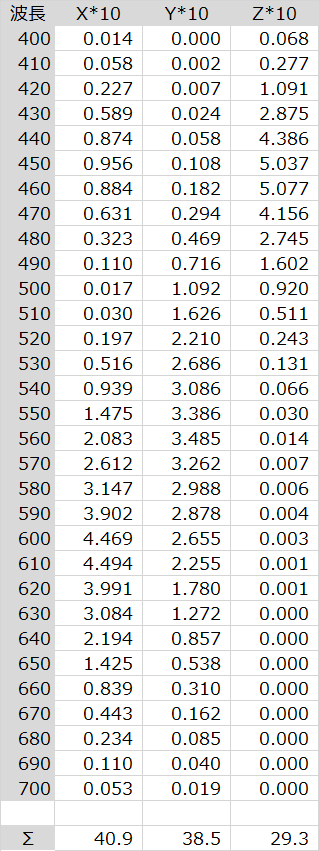
　足し合わせると、X＝40.9、Y＝38.5、Z=29.3となりました。このように足し算していいのも、グラスマンの加法則があるからですね。

　短冊状に切った長方形の面積を足し合わせる処理は、Σ（シグマ）を用いた↓のような式で表現されます。色彩系の検定でも出てきますが、∫(インテグラル)を用いた積分の式の実用版といったところです。

⑤係数kを求める

　これで完了と思いがちですが、係数kを忘れてます。

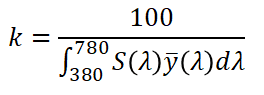
　kの分母に注目すると、ここにはあるものが隠れて(省略されて)います。

　　それは、分光反射率R(λ)です。なぜ隠れているか？というと、表示しても意味がないからです。