
色を科学する その⑧ 色覚の多様性が色彩学の難題を解くカギ<前編>
色覚多様性(いわゆる色覚異常)が色彩学100年にわたる難題であった「ヒトの目の感度」=錐体分光感度を知るカギになったというお話。長いので<前編>と<後編>に分けて書きます。
色彩学100年にわたる難題
残念ながら、等色関数はヒトの目の感度、すなわち錐体分光感度ではなく、それを"間接的"に表すものです。1900年代前半では、錐体分光感度自体やそれを調べる方法も確立できておらず、等色実験により"間接的に表すもの"を求め、1931年に制定して、代替として使ってきたという次第です。
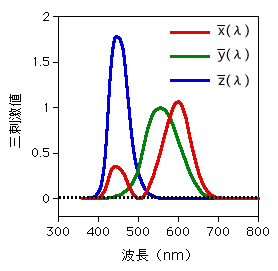
しかし、1800年代には既に、ヤング(Thomas Young)とヘルムホルツ(Hermann von Helmholtz)により、赤、緑、青に感度を持つ3種類の視細胞(錐体)が網膜にあるという三色説が唱えられていました。錐体分光感度は1970年ごろにようやく精度よく求めることができたので、約100年かかってやっと念願を達成できたのです。

※ここでは、敢えて、L, M, S錐体ではく、R, G, B錐体として話を進めます(理由は後ほど、CIE RGB表色系とは異なるので注意)。
錐体の色度座標がわかれば、、、
"間接的"をかみ砕くと、等色関数は錐体分光感度の線形変換になっています(ルータの条件)。だけど、その係数がわからなかったのです。しかし、この状況は、線形代数学で言う「基底変換」であり、下図のように、XYZとRGB錐体の互いに空間の軸(原刺激)の角度がズレているだけなのです(↓これはあくまでイメージ、実際にはこういう関係でないです)。
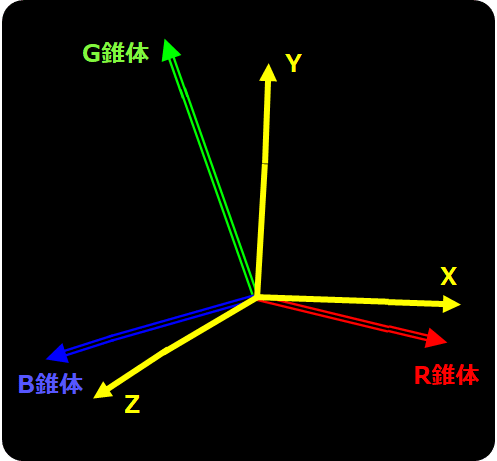
そして、これらの空間内の任意のベクトル(=三刺激値)の線形変換式(の係数)は、原刺激の色度座標から求めることができます。厳密にいうと、求めたい(この場合RGB錐体の)表色系の原刺激の、既知の表色系(XYZ)における、色度座標です。
その理論を説明すると・・・
※太字が原刺激、標準体が三刺激値(原刺激の量)を表してます
任意の色Cに対するXYZおよびRGB錐体空間での下記等色方程式と、
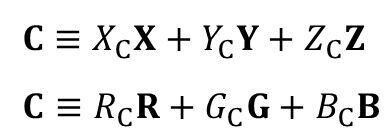
X=Y=Z=1の単位面(色度図の面)での下記等色方程式から、三刺激値だけに注目して抜き出して整理すると・・・
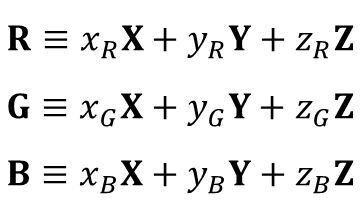

下記、変換行列が得られ、逆行列化することにより、RGB錐体のXYZ表色系での色度座標から、XYZ三刺激値→RGB錐体三刺激値への変換が可能となります(導き方の詳細は省略します)。
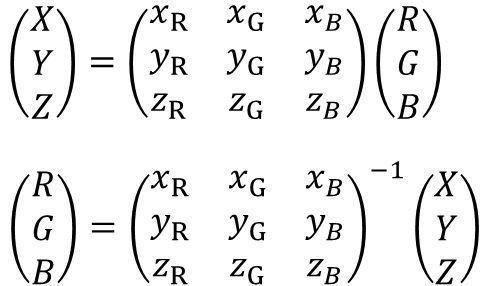
実際には三刺激値の単位の取り方により係数が必要なので、下記のような形になります。これは等色関数(=スペクトル三刺激値)にも有効です。

いずれにせよ、RGB錐体のxy色度座標がわかれば、RGB錐体空間の等色関数=錐体分光感度がわかるとなりました。
見分けられない色のその先にある!
色覚多様性(色覚異常)の方が、特定の色同士を見分けにくいことは、経験的にわかっていました。この現象をベクトルで幾何学的に考えると錐体色度座標を見つける手掛かりになります。
例えば、GとB錐体座標の色を適当な比率で混ぜ合わせた色C1(GとB錐体が適当な比率で応答する色と呼ぶべきか)を考えます。この色C1はGとBを結ぶ直線状にあります。ここに、Rをどんどん足していくと、下図のようにC1とR錐体の色度座標とを結ぶ直線状を移動していき、最終的にはR錐体の座標と合致します。
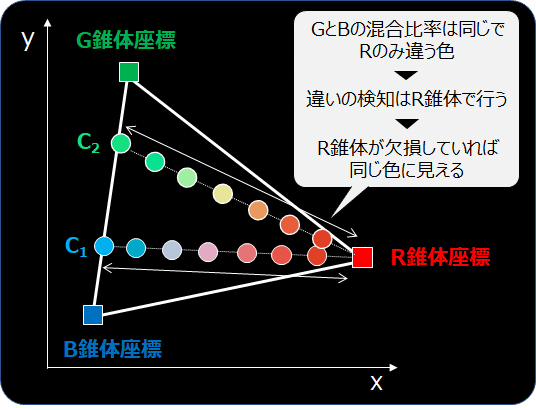
ここで、C1とR錐体座標を結ぶ直線状の色は、GとBの比率が同じで、Rだけ異なる、すなわち、Rの違いで見分けているので、もしR錐体が欠損していると、見分けることができず、同じ色に見えてしまいます(「二色型第一色覚異常」、今は「1型2色覚」と呼ぶようです)。これらを混同色(Color Confusion)と呼び、それらをむすんだ直線を混同色軌跡(Confution Loci)と呼びます。
さらに、GとBの比率が異なる別の色C2でも同様に混同色軌跡が引けます。混同色軌跡はどんどん引けるのですが、当然、R錐体座標に集まります。
よくよく考えると、R錐体の座標がわからず、それを見つけようとしていたのでした! なので、複数の混同色軌跡交わる点、混同色中心(Center of Confution)が、R錐体座標ということなのです!
つまり、GやB錐体についても同様にそれらが欠損している色覚多様性の方の混同色を調べていけば、座標がわかり、錐体分光感度もわかるのです。
混同色をコツコツ調べるのは大変なので、実際には色覚多様性の方の等色実験結果を用います。詳細は<後編>で。少々お待ちを。
今では、「色覚多様性」と呼ぶようになり差別は少なくなりましたが、以前は「色盲」と呼ばれて、差別されてました。私も「多様性」の範疇に入るのでお気持ちは察します。そのような方々による実験により、100年間解明できなかった錐体分光感度がわかるってのが、ドラマチックですね。失って初めてその大切さや意味がわかるってやつでしょうか?
いいなと思ったら応援しよう!
![[色彩工学/カラーサイエンス]YoshiColor](https://assets.st-note.com/production/uploads/images/12365218/profile_38f7a1125cd491b5b5e80c13ba3ef3d9.jpeg?width=600&crop=1:1,smart)
![[色彩工学/カラーサイエンス]YoshiColor](https://assets.st-note.com/production/uploads/images/12365218/profile_38f7a1125cd491b5b5e80c13ba3ef3d9.jpeg?width=60)