三角比の覚え方（０°≦θ≦９０°）

有名な覚え方らしいのですが、忘れないよう、メモ。

■まず下のような表を書きます。

横に０°、30°、45°、60°、90°、
縦に　sin　cos　tan　と書き、
sin　の欄に√／２　と書きます。

■ルートの中に、左から順に、０、１、２、３、４、と書き入れます。

【√０/２】は【０/２】なので、０と書き直します。
【√１/２】は【１/２】なので、１/２と書き直します。

なので、そのままにしておきます。
　　　　　　　　▶分母の有理化

sin90°は次の様になります。

此処までで、
　sin 0°＝０
　sin30°＝１/２
　sin45°＝√２/２　（１/√２）
　sin60°＝√３/２
　sin90°＝１
とわかりました。

cos の欄は、
　cos 0°に 1=sin90°
　cos30°に√３/２＝sin60°
　cos45°に√２/２＝sin45°
　cos60°に１/２＝sin30°
　cos90°に ０＝sin 0°
と、書き入れます。
　　　▶ sin と同じ要領で全ての欄に √／２ を書き入れ、０°から、
　　　　ルートの中に ４、３、２、１、０ としても構わないと思います。

tan は、分母に cos の分子、分子に sin の分子を入れます。

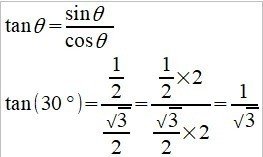
　cos の値を分母に、sin の値を分子に入れて、
　分子分母に２を掛けて約分すると、tan の値になります。

それぞれ書き込んだものです。
　　　　　▶tan45°は、sin45°＝cos45°＝１/√２とすると、１／１＝１

最後にまとめると、

表の出来上がり。

・・・。
・・・・・・。
・・・・・・・・・。

三角形書いた方が間違いないような気もするのですが、
sin の処だけ覚えておけば、手っ取り早いのかな・・・？