
都立進学校の重力モデル(前編:構築・検証)
受験における地理的影響に興味を持ち、ここ数回は都立進学校の通学時間の影響を分析しています。
この分析対象の都立進学校は、進学指導重点校と進学指導特別推進校の14校です。この次の進学指導推進校になると、最難関大学への合格者が二段落ちるので、この14校を都立進学校として定義しています。
◆進学指導重点校(7校)
日比谷、西、国立、戸山、青山、立川、八王子東
◆進学指導特別推進校(7校)
小山台、駒場、新宿、町田、国分寺、国際、小松川
今回の記事では、これまで集めたデータを元に都立進学校へ重力モデルを適用し、理論値と実際値の検証を行います。その上で、次回に都立上位校への学力上位層の集中がどの程度起こっているか(輪切り効果はあるのか)という分析を行います。
0. まとめ
都立進学校の市区別生徒数に対して重力モデルは概ね適用できる。サンプル3校での決定係数は0.4438〜0.8504(平均0.6032)。
市区別生徒数が距離(通学時間)の2乗に反比例する場合、引力係数が最も大きいのは国分寺高校、最も小さいのは新宿高校。これは国分寺高校は広い範囲から生徒を集める力が最も大きく、新宿高校はその力が最も小さいことを意味する。
1. 重力モデルとは
ニュートンの万有引力の法則は、物質の間の引力がそれぞれの物質の質量に比例し、距離に反比例することを示す法則(方程式)です。これを社会科学に適用し、二つの対象の間のある説明変数が、対象それぞれの変数に比例し、対象間の距離に反比例する場合の説明モデルが、重力モデル(gravity model / gravity equation) です。
社会科学分野で重力モデルを適用した代表例は国際貿易(国際経済学・計量経済学)です。国家間の貿易額は、両国家のGDPの積に比例し、距離に反比例するというものです。この他にも重力モデルは人の移動や国際電話の発着回数などにも当てはまるようで、社会科学の色々な分野で取り上げられているようです。
受験においては、私の過去の記事で大学進学にも当てはまることを確認しています。
今回、東京都の都立高校受検に重力モデルを当てはめるに当たり、「都立進学校への市区からの入学者数は、高校定員と市区の公立中3年生徒数の積に比例し、距離の2乗に反比例する」という設定をすることにします。距離の乗数は2に固定し、その代わりに引力を示す定数(引力係数)を学校ごとに異なる数字として導出します。
今回適用する重力モデル式を具体的に書くと、このようになります。

2. 引力係数の計算結果
これまで集めたデータを上記の重力モデル式に投入して、学校ごとの引力係数(Gi)を計算すると、このようになります。

さて、この表にある引力係数は何を意味するのでしょうか? 引力係数は「もしも高校間の差異が全くない場合に、東京都市区部の公立中3年生全体(約7.7万人)が、距離(通学時間)だけで高校を選ぶ場合、その高校がどれだけ多くの受験生を引き寄せるかという指標」です。そのため、引力係数が大きいと、より広い範囲から生徒を集める力が大きいことになります。
例えば、西高校の引力係数は0.0282、新宿高校の引力係数は0.0115です。これに対し、練馬区から西高校への通学時間も新宿高校への通学時間も40分で同じです。この時、高校間の差異が全くない前提では、練馬区の公立中3年生(4,590人)は、新宿高校よりも西高校に入学する生徒が多い(0.0282÷0.0115≒2.5倍)となります。
この観点で改めて表1を見ると、引力係数が最も大きい国分寺高校(0.0361)は生徒を広い範囲から集める力が最も大きい高校となります。逆に、引力係数が最も小さい新宿高校(0.0115)は生徒を広い範囲から集める力が最も小さい高校となります。新宿高校は前々回の記事で、市区部の公立中学生が最も通学(アクセス)しやすい高校であったことを考えると、引力が低くても定員を充足できる生徒を集められるとも解釈できます。
実際には、高校ごとに校風・施設・環境も違うし、学力レベルも異なります。特に東京では、進学指導重点校/特別推進校/推進校などの区分けも行っています。そのため、実際の各高校の生徒の市区の分布は、この重力モデル式で計算された理論値通りにはなりません。そこで、実際値と理論値にどの程度の差があるのかを検証してみます。
3. 重力モデルの検証
今回の分析対象の14校の学校案内パンフレットを見ると、西・戸山・町田の3校では居住市区町村別の生徒数が掲載されていました(町田は出身中学別)。その数字を1/3にして1学年あたりの市区町村別の生徒数概算値を算定し、それを実際値として扱います。
その上で、重力モデル式から計算される理論値と対比して見ていきます。なお、理論値を回帰モデルの予測値と見なして、決定係数も計算しています。
①西高校
西高校は近隣の杉並区・世田谷区・練馬区・三鷹市・武蔵野市・中野区などから自転車で15〜40分程度で通学できます。そのため、理論値(ブルーの折れ線)でも実際値(イエローの菱形)でも、これらの市区からの通学生徒数が大きな値となり、グラフ左側に寄っています。
また、実際値を右に見ていくと、遠方で公立中生徒数が少ないの市区(グラフ右側)にも少数ではありますが、実際に通学する生徒がいるようです。
結果として、理論値と実際値の分布はほぼ同じ形となり、決定係数は0.854と高い値となりました。

②戸山高校
戸山高校は理論値(ブルーの折れ線)と実際値(イエローの菱形)の間に、一定の乖離が見られます。特にお膝元の新宿区や隣の豊島区からは生徒数のギャップが大きいようです。
そもそもとして公立中3年の生徒数が新宿区(997人)や豊島区(920人)がそれほど多くないのに対し、重力モデルでは距離の2乗の反比例影響が大きく出て、理論値人数が大きな数字で算定されるのが要因と考えられます。
それ以外にも理論値で5〜10人程度の市区でも外れ値がいくつも存在することも影響して、決定係数は0.4438と低い値となっています。

③町田高校
東京の市区部の公立中学生にとって、もっとも通学アクセスが悪いのが町田高校でした。それが理論値の折れ線グラフに現れており、町田市以外からはほぼゼロというL字型となっています。
そして、実際値を見ても、町田市の生徒が突出し、次に八王子市が来て、以降は0人の市区が数多く並ぶため、理論値に近い実際の分布となっています。
その結果、決定係数は0.5155と2番目に高い数字となりました。寡占化している町田市の数値の差の全体影響が大きいので、伸び悩んだ印象はあります。

4. 最後に
重力モデルの理論値と実際値の検証結果を見ると、決定係数は0.4438〜0.8504(平均:0.6032)となりました。高校ごとに凸凹はありますが、都立進学校の市区別生徒数に対して重力モデルは概ね適用できると言えそうです。
ただし、高校に最寄りの市区(学校所在地)では、理論値>>実際値の傾向も確認されています。ここはモデルの改良余地がありそうですが、一旦は重力モデルをそのまま使うことにします。
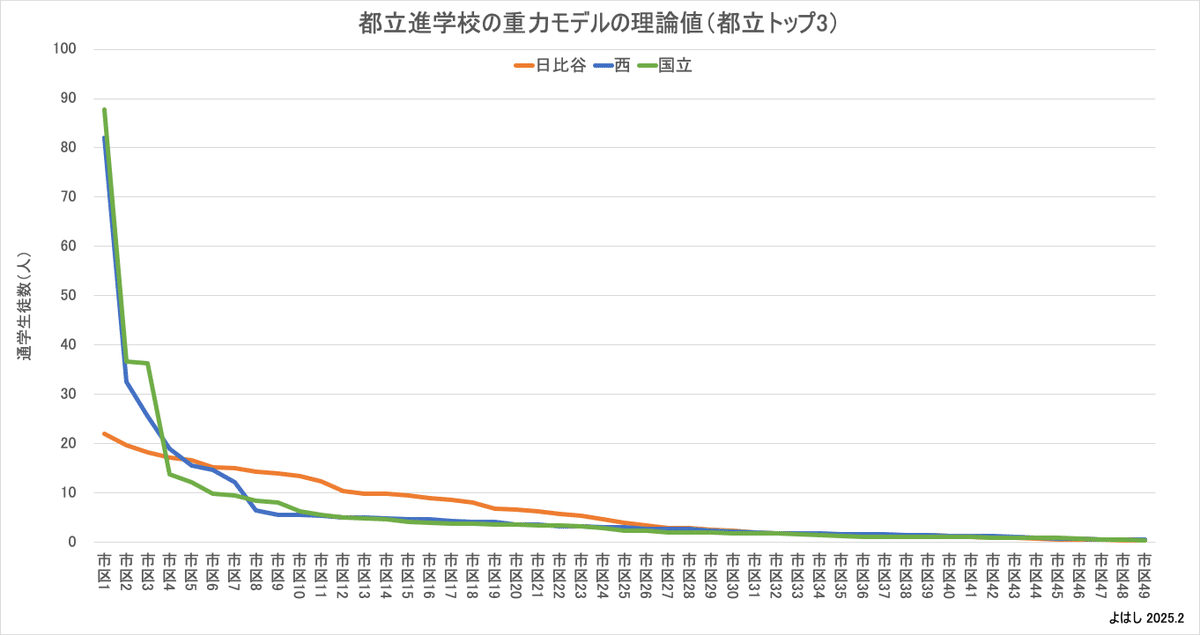
なお、都立トップ3(日比谷・西・国立)の理論値を1つのグラフに集めると、日比谷(オレンジ)は他の2校に比べてカーブが緩やかで、市区の偏りが少ないことがわかります。これは日比谷は市区別の通学時間の差が小さい一方で、近隣の市区の生徒数が少ないため、理論上では生徒数が多い市区に程よく引力を働かせながら生徒を集めることを意味します。
逆に、西や国立はアクセスは平均的な中で、近隣に生徒数が多い自治体があるため、理論上ではそうした市区からの生徒を中心的に集めていると考えられます。あくまで理論値ですが、そこそこ肌感覚に近い印象です。
ここまでは、市区部の公立中学生全体への重力モデルの適用でした。次は学力レベルを層別して、学力上位層への引力がどの程度歪められているのか(輪切り効果あるのか)を分析してみます。
