
都立・進学指導重点校の合格最低点推定モデルの計算方法の解説
過去に都立高校(進学指導重点校)の合格最低点を推定する記事を書きました。また、受検者平均点が公表された後には、検証も行っています。
これらの記事は受験が近づくとそこそこ読んでもらえるのですが、記事内のロジックや数字が妥当なのかをチェックしてくれる方はほぼいない(過去に1名のみ)という状況でした。1人でレビュワーなしで分析した内容を記事にしているので、誰もチェックしてないのは、ちょっと不安でした。
そうした中、今週になってロジック検証してくれる方が出てきました。Excelで計算の再現をしようとしたとのことです。
反証可能であってこそ科学的です。私が趣味で作っている推定モデルを検証してくれる方がいるのは感激ですし、大変ありがたいです。
もしかしたら、これから受験本番が近づくにつれて、このシリーズを読んでくれる人も増えるかもしれません。また、モデルを検証してくれる人も増えるかもしれません。そこで、改めてモデルの組み立て方と計算方法の解説を書いてみます。
1. 都立・進学指導重点校の一般入試の基礎知識
都立の進学指導重点校は、日比谷・西・国立・戸山・立川・八王子東の7校です。これらは、東京一工・地帝・早慶に生徒の2〜6割が進学する進学校です。この7校の一般入試は次のようになっています。
英数国の3教科(各100点)は高校ごとに作成する自校作成問題
理社は都立高校入試の共通問題(各100点)
英数国理社の5教科500点満点を総合得点700点に換算(少数以下は切り捨て)
内申点は副教科4教科は2倍にした換算内申65点満点を総合得点300点に換算(少数以下は切り捨て)
事前実施のスピーキングテスト(ESAT-J)は総合得点20点
学力検査(5教科)700+換算内申300+スピーキング20=1020点満点の総合得点で合否を判定
このような入試に対して、受験業界にいない素人が入手できるのは、①高校ごとの受検者倍率、②高校ごとの3教科の受検者平均点(HP・学校案内や学校説明会資料など)、③都立高校入試全体の理社の受検者平均点(東京都が公表)くらいです。
塾によっては④高校ごとの理社の受検者平均点も入手しているようで、②③④セットで資料をもらえるところもあるようです。例えば、こちらの塾(プラスジムさん)は過去データも整理してくれています。
https://www.plusgym.jp/blog/metropolitan-high-school/180725average/
逆に言えば、高校ごとの合格者最低点や合格者平均点は公表されていません。でも、受験生が知りたいのは、受検者平均点よりも合格最低点のはずです。そのため、入手できるデータから合格最低点を推定してみようと考えて、試行錯誤している内容を記事にしたのが一連のシリーズです。
2. 合格最低点の推定モデルの考え方
上記のように都立高校入試では受検者に関する数字は入手できるので、それらから合格最低点を推定するモデルを作っています。その際、合格最低点は、大きく分けると次の4つの要素で決まります。
①高校ごとの3教科点数
②都立共通の理社の点数
③換算内申の点数
④スピーキング(ESAT-J)の点数
変数が4つもあるとモデル作って計算するの複雑になります。そのため、②③④は高校によって異なるが年度変動しない定数として割り切って、変数を①3教科得点だけにしています(ただし、2024年度入試では理社が10年に1度の易化だったため、理社の定数は最後に調整する形に改良しました)
この場合、唯一の変数の①3教科点数に対して合格最低点が決まれば、総合得点の合格最低点も決まります。3教科の合格最低点は公表されていないのですが、受検者平均点と受検者倍率がわかれば、受検者分布を正規分布と仮定して標準偏差を定数設定することで、ある程度の精度で推定できるはずです。
さらに、受検者倍率は当日に定員に対する倍率が公表され、合格発表後に合格者数に対する実質倍率が公表されます。そうなると、受検者平均点さえわかれば、総合得点の合格最低点を推定できることになります。
このような考え方で、合格最低点を計算するのが、私が行っている都立・進学指導重点校の合格最低点の推定です。
コメント欄に理社と内申点の定数の算定方法についてご質問をいただきましたので、簡単ですが解説を記載しております。興味のある方はコメント欄をご覧ください。
3. 合格最低点の推定値の計算手順
この推定モデルで、どのように合格最低点の推定値を計算しているのかを、日比谷高校の2024年度入試を題材にして説明します。
①受検者倍率から最下位合格者の累積比率を算出
受検者の分布の中で、最下位合格者が上位何%の位置かを計算します。受験者倍率をm倍とする場合、最下位合格者の上位からの比率p%=1÷mです。倍率2倍なら1÷2=0.5(上位50%)、倍率3倍なら1÷3=0.33(上位33%)、倍率1.25倍なら1÷1.25=0.8(上位80%)です。
日比谷2024年度入試の場合は倍率1.32倍なので、1÷1.32=0.758(上位75.8%)です。この倍率なら受検者の上から75.8%まで合格できる(=不合格は下位24.3%)ことを意味します。
②3教科合格最低点の偏差値を計算
続いて、受検者全体を母集団とした時の、①で計算した最下位合格者の得点の偏差値を計算します。
このモデルでは、理社・内申点・ESAT-Jは高校ごとの定数にしているので、最下位合格者の3教科得点は、合格者の3教科得点分布の最低点数なります。また、受検者の分布は正規分布を仮定しています。そのため、Excelで計算する場合は、最下位合格者の累積比率p%に対して、3教科合格最低点の偏差値SS=norminv(1-p%, 50, 10)で計算できます。
1つ目の引数は、p%でなく1−p%です。この関数の引数は下からの累積確率のため、そのままp%を入れると、上位p%ではなくて下位p%の偏差値になってしまいます。そのため、引数は1-p%と変形させる必要があります。
2つ目と3つ目の引数は平均:50、標準偏差:10を設定しています。③で使う平均(X)と標準偏差(σ)を使えば、②③を1回の計算で行って3教科合格最低点を算定できます。ただ、最下位合格者の偏差値を一度見てみたいので、この計算過程を入れています。
日比谷2024年度入試の場合には、m=75.7%のため、最下位合格者の偏差値SS=norminv(1-75.8%, 50, 10)=43.0となります。倍率が1.32倍と2倍未満のため、受験者平均点より下に合格最低点が存在し、それは受験者の中で偏差値43.0の位置ということを示しています。
③最下位合格者の3教科得点の計算
次は最下位合格者の3教科得点の計算です。今回は正規分布を使っているので、倍率に応じて合格最低点の偏差値が変わります。逆に言えば、平均点と標準偏差がわかれば、その偏差値から合格最低点を計算できます。
細かい説明は省略しますが、平均X、標準偏差σの正規分布においては、次の図のようになります。
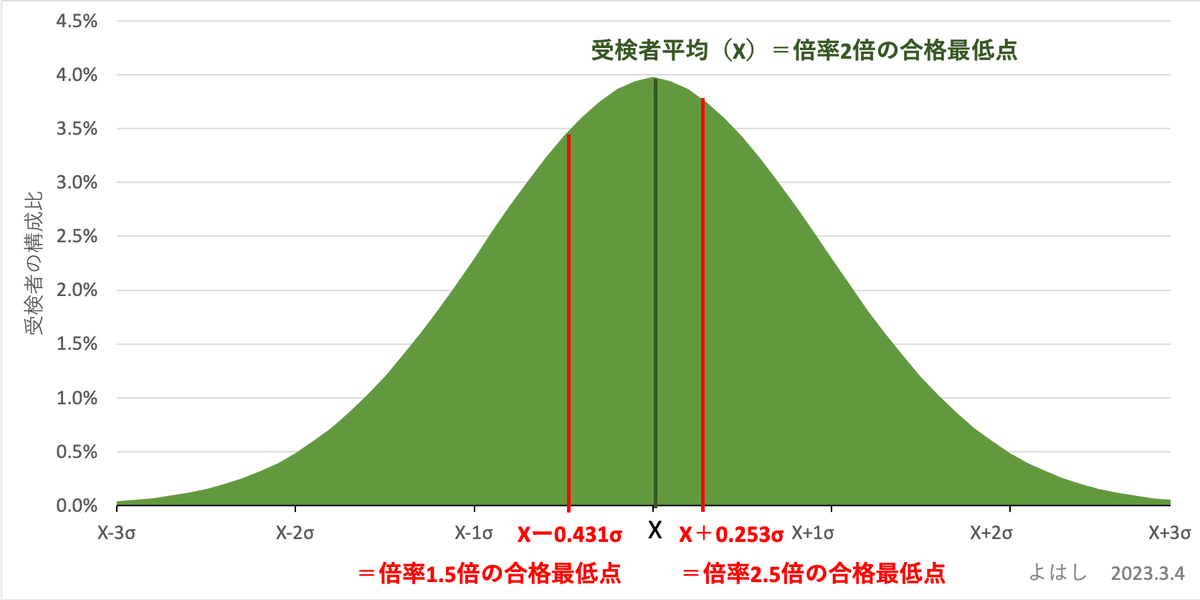
倍率2倍の場合
最下位合格者の偏差値は50。山の中央の黒い線で、合格最低点=X(平均と同じ)倍率2.5倍の場合
最下位合格者の偏差値は52.53。山の右の赤い線で、合格最低点=X+0.253σ倍率1.5倍の場合
最下位合格者の偏差値は45.69山の右の赤い線で、合格最低点=Xー0.431σ
では、日比谷2024年度入試で計算してみましょう。
入手した科目別受検者平均点から計算すると、3教科の受検者平均点X=英58.5+数62.0+国63.1=183.6点です。受検者標準偏差σは、子供の塾の追跡データなども参考に、定数としてσ=25で設定します。この時、日比谷の合格最低点の偏差値は43.0=50.0-7.0=50.0-0.70×10であるため、日比谷の3教科合格最低点L=183.6ー0.70×25=166.2点となります。
なお、実際の私のExcelシートでは②③をセットにして、3教科合格最低点L=norminv(1-p%, X, σ)のように一回で計算しています。この計算でも、L=norminv(1-75.7%, 183.6, 25)=166.2です。
④定数を加算して総合得点の合格最低点を計算
ここまで来たら、あと一歩でゴールです。
都立高校の総合得点は学力検査(5教科)700+換算内申300+スピーキング20=1020点満点なので、あとは理社と換算内申とスピーキング(ESAT-J)の点数を足して計算するだけです。理社(=R)、換算内申(=N)、ESAT−J(=E)はいずれも高校ごとの定数としているので、変数である3教科得点(v)を用いて、総合得点TはExcelで次の式で計算できます。
T=rounddown((v+R)×700/500, 0)+rounddown(N*300/65,0)+E
この時、R、N、Eは定数なので、3教科最低点Lの時に、Tは合格最低点minTとなります。よって、minT=rounddown((L+R)×700/500, 0)+rounddown(N*300/65,0)+Eで合格最低点を推定できます。
日比谷の場合は、子供の塾の追跡データなどから、R=170、N=61.5、E=19で定数設定したため、L=166.2点を入れて、日比谷2024年度入試の合格最低点minT=rounddown((166.2+170)×700/500, 0)+rounddown(61.5×300/65, 0)+19=772点と一旦は推定できます。
⑤理社の補正
上記で概ね計算できるのですが、理社が極端に難化したり易化したりすると、理社の得点を定数Rで固定できなくなります。2024年度入試が極端に易化したので、このパターンに当たりました。都立高校入試全体で理社の平均点は122.3点(単純合算)ですが、これは過去15年平均114.4点より+7.9点となります。

この理社の著しい上振れを調整して、日比谷の合格最低点minTは最終的には、minT=rounddown((166.2+170+7.9)×700/500, 0)+rounddown(61.5*300/65,0)+19=783点と推定しました。
なお、この調整は都立高校入試の平均点が発表されるまで実施できません。そのため、来年度以降の試験直後の速報版では、上下10%を除く80%の幅に治まる±7.2点(総合得点で約10点)の推定補正を加える形にする予定です。
4. 合格最低点の推定値一覧(2024年度入試)
進学指導重点校の7校について、上記のような計算を行った結果がこの表です。定数は塾の追跡データと照らし合わせて、最終的にはこのようにしています。ただ、追跡データとは完全に一致させるまでの定数補正は行っておらず、キリのいい数字に設定したので、±5点くらいの誤差はあると考えられます。

5. 最後に
繰り返しになりますが、この推定モデルは、受験者の分布を正規分布と仮定して、いくかの変数を定数で代替した簡易計算のモデルです。塾の追跡データと多少の整合チェックはしていますが、完全に一致させるまでの補正は行っていないので、推定値には誤差もあります。あくまで一つの参考値として見てください。
なお、冒頭に記載の通り、数字やロジックが怪しいところのご指摘は歓迎です。間違っていたら、モデルを修正していくので、遠慮なく教えてもらえると有り難いです。
追記
過去6年分のボーダー推定値の記事を更新しました。
