駿台偏差値52の男子が早慶附属高校を最大数受験し、最低1校に合格できる可能性は58%
趣味の統計分析で、受験データを対象に分析しています。ただ、統計分析というよりも、データ整理とモデル作りが近いです。前回は駿台中学生テストのデータを参考にして、高校受験の合否分布のモデルを作りました。今回はその続きです。
以下では、明示がなければ、模試の偏差値は高校受験の駿台中学生テストの偏差値です。
1. 合否分布の発生メカニズム
合否分布のグラフは、模試の同じ偏差値の受験生の合格と不合格の人数の分布です。合格可能性の判定偏差値(A判定80%など)は、この分布からを算定しているようです。模試はあくまで模試であり、入試本番のテストとは異なるため、同じ模試の偏差値の受験生でも、合否が分かれるのは自然な話だと思います。
では、模試と入試本番の成績の差は何に起因するのでしょうか?
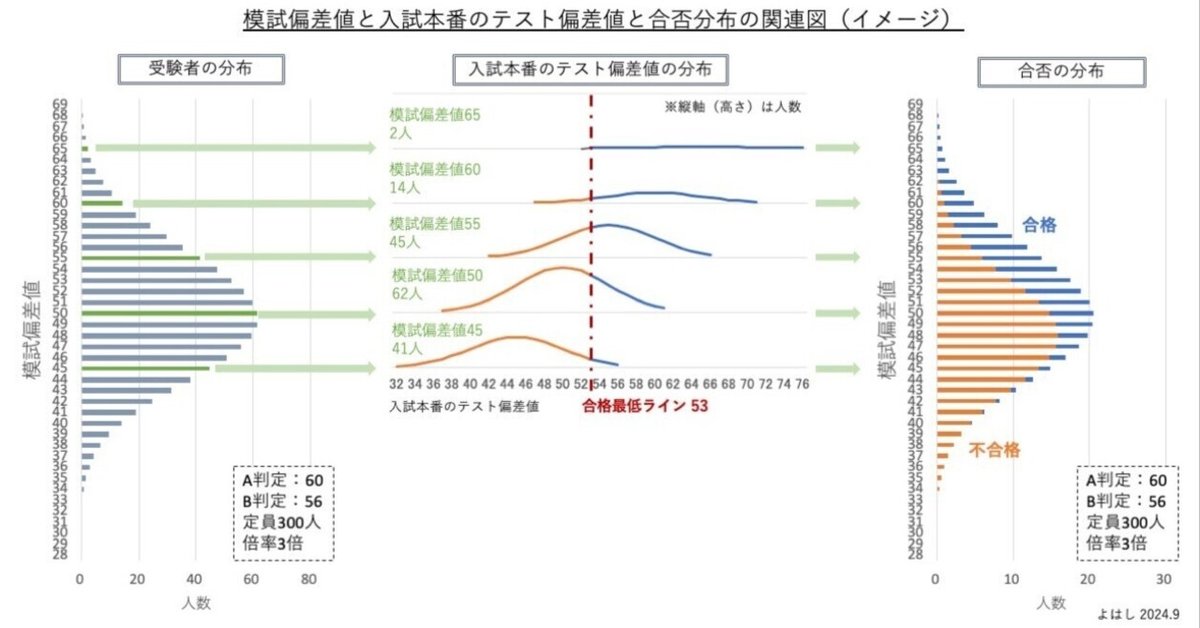
そもそもとして、学力が同じでも試験内容によって成績は変動します。また、模試を受けた時点から入試本番までの間での、相対的な学力の増減もあります。こうした変動や増減によって、模試の偏差値が同じでも合否が分布することになります。このような合否分布の発生メカニズムをイメージにするとこのようになります。

左の棒グラフが受験者の模試偏差値に応じた人数分布です。前回の基本パターンのA判定(確実圏・合格可能性80%)で倍率3倍のモデルです。偏差値ごとの人数規模がある程度ある方が説明しやすいので、この図では定員を300人にしています。
左の棒グラフから、模試偏差値が45、50、55、60、65の標本を抜き出してみます。グリーンの棒グラフのところです。例えば、模試偏差値45の標本ですが、この標本に含まれる受験生は、模試を受けた時点では偏差値45で同じですが、入試本番のテストの結果は、上記のような要因により上下に分布します。この当日の分布を示したのが中央の折れ線グラフ(オレンジとブルー)です。
このように、それぞれの標本内で当日のテスト結果が上下に分布して、母集団(受験者全体)で成績が上から定員までが合格になります。このモデルの場合、偏差値53で定員に達するため、中央の折れ線グラフは、入試本番テストの偏差値が53以上なら合格でブルー、それ未満なら不合格でオレンジと色を変えています。
このような成績の変動を得て、入試本番のテスト結果(テスト偏差値)で合否が決まり、その合否を模試の偏差値別に集計すると、図の右のような合否の2色の分布となるのです。
ポイントは、模試の持ち偏差値に対して、一定の変動で生じて、入試当日のテスト結果(テスト偏差値)が分布するというところです。このメカニズムを是とする場合、「一定の変動」を推定できれば、持ち偏差値ごとに高校(A判定○%)の合格可能性を算定できるはずです。
2. 入試本番の偏差値変動のモデル化
入試本番のテスト結果(テスト偏差値)が模試の持ち偏差値から上下にブレる要因は、上述の通り大きく2つです。1つは、テスト内容によってテストの実施ごとに生じる短期的(ランダム)な変動。もう1つは、模試を受けた時点から入試本番までの、相対的な学力の変動による結果の変動です。
後者の学力変動は後で考察するとして、前者のテストの実施ごとのランダムな変動は、子供の塾の毎月のテストの2連続の結果データを用いて計算してことがあります。この塾の毎月のテストは、駿台中学生テストとほぼ同じくらいの母集団=難易度です。そのため、今回はこの時の分析結果を、1つの目のテストごとの短期(ランダム)変動として採用します。
このサンプルデータをグラフにすると、次のブルーの棒グラフです。概ね中央に凸の左右対照の形をしています。少し中央が凸凹していますが、正規分布に見えなくはないです。このサンプルデータの分布の標準偏差(σ)は6.1でしたので、σ6.1で正規分布グラフを作成すると、グリーンの折れ線となります。多少凸凹していますが、そこそこサンプルデータにフィットしている印象です。

これで、2つの変動要因のうち、試験ごとのランダムな変動の分布モデルを入手できました。まずはこの変動要因に限定して、模試と入試本番の偏差値の関係をシミュレートしていきます。なお、サンプルデータの傾向から、入試本番の偏差値変動の幅は上下±14に限定しています。
3. 模試偏差値ごとの合否分布のシミュレーション
①サンプルデータと同一の変動の場合
模試の持ち偏差値(縦軸)ごとにサンプルデータと同じ変動をさせた時、入試本番のテスト偏差値(横軸)がどう変化するのかをシミュレートすると、この表のようになります。

基本モデルの確実圏(A判定・合格80%)の偏差値が60、可能圏(B判定・合格60%)の偏差値が56、倍率3倍にしています。定員は100人でプロットしています。計算を簡易的に行うので、変動幅は持ち偏差値±14、入試本番のテスト偏差値は25〜75の範囲としてます。
この基本モデルの場合、ボーダーは偏差値53なので、入試本番のテスト偏差値が53のところで合否を分けています。ブルーが合格、オレンジが不合格です。
右端に持ち偏差値ごとの合格率(合格者数÷受験者数)を計算しています。ところが、確実圏の合格率が91%、可能圏では71%となり、設定値(80%/60%)から大きく外れています。つまり、合否の分布モデルと入試本番の偏差値変動モデルの間にギャップがあることになります。
②正規分布(σ:6.1)で変動の場合
同じように模試偏差値と入試本番のテスト偏差値の関係を表にすると、このようになります。

右端を見ると、確実圏の合格率は90%、可能圏は70%です。サンプルデータの分布より少し設定値(80%/60%)には近づきましたが、まだまだギャップがあります。正規化しても、合否の分布モデルと入試本番の偏差値変動モデルの間にギャップは埋まりません。
これらを通じて言えることは、入試本番の変動は、試験後とのランダムな変動(要因①)だけでは説明できず、当日までの学力変動(要因②)の影響を無視できないということです。当たり前と言えば当たり前ですが。
そのため、逆算で合否分布モデルと整合する入試本番の偏差値変動モデルを計算してみます。
③合否分布モデルと整合する入試本番の偏差値変動モデル
サンプルデータの変動モデルでも正規分布(σ:6.1)の変動モデルでも、確実圏・可能圏の合格率が設定値より上振れしていました。これは不合格者が不足しているということであり、もっと分布が下に厚みがあることになります。つまり、入試本番の偏差値変動はこれまでの想定よりも大きいということです。
そこで、正規分布モデルの標準偏差(σ)を増やしながら、確実圏の合格率が80%になるσを探しました。結果として、σ:7.8の時に、確実圏の合格率が80%となり、分布モデルと一致しました。

この場合、可能圏の合格率は64%とまだギャップはあります。また、下端の累積の合格者数もボーダーでは109人と定員100人を少しオーバーしてます。今回のシミュレーションでは、模試の持ち偏差値によらずに入試本番の偏差値変動は同じモデルにしていますが、実際は模試偏差値の高低によって、入試本番の偏差値変動の分布が少し違うのかもしれません。
ただ、そこまで精緻に変動モデルを作っても、整合先の合否分布モデルが正しいかもわからないので、今回は入試本番の偏差値変動は模試偏差値によらず一定で、標準偏差7.8の正規分布(ただし±14の幅)を採用することにします。変動のグラフはオレンジの折れ線となります。

4. 模試の持ち偏差値からみた志望校の合格可能性
変動モデルが正規分布(σ:7.8)での入試本番のテスト偏差値の分布を改めてみてみます。

この表を使うと、自分の模試の持ち偏差値に対して、当日のテスト偏差値がどの程度になる可能性があるかを計算できます。例えば、確実圏偏差値60・倍率3倍の高校の受験者分布における、持ち偏差値が50の受験生(受験者平均と一致)を考えます。変動モデルを上下変動±14で設定しているため、この受験生の入試本番の偏差値は36〜65に分布します。
この場合、偏差値65に到達するのは、同じ持ち偏差値の受験生20.5人のうち0.2人なので、かなり難しいことがわかります。一方、この高校の合格最低ラインは偏差値53であり、当日にこれを超える可能性は7.0人/20.5人=34%となり、ある程度の可能性があることがわかります。
前回の合否分布モデルだと、確実圏偏差値60・倍率3倍の高校での模試偏差値50における合格率は28%でした。少し差が出ていますが、平均すれば約3割くらいだと判断できると思います。
5. 早慶附属高校に少なくとも1校は合格できる可能性
表3の分布は確実圏偏差値60・倍率3倍の高校の設定です。前回の分析の通り、合否の分布=受験者の分布は確実圏偏差値の高低で違うのですが、60前後は同じような分布でした。
そのため、確実圏偏差値が60前後の高校は、表3を上下に数字をシフトさせて合格率の数字を入手できます。例えば、模試の持ち偏差値50の時に、確実圏偏差値62の高校の合格率を知りたいのであれば、縦軸は50ではなく48の行にある合格率の数字となります。
このように表3を使うと、次の文章の検証が可能になります。
早慶附属高校を連続で最大数受験することを前提として、その中で一つの早慶附属高校に合格した過去の受験生の、駿台模試の偏差値の下限(ボーダー)は五二〜五三程度である。
では、男子と女子に分けて計算してみましょう。計算にあたり、駿台中学生テストの判定偏差値は最新の2023/2024年版(2024年5月付け)、倍率は2024年度入試のものを用います。なお、早稲田学院(女子)は倍率4倍を超えるので、倍率3倍のモデルではなく、倍率4.5倍のモデルから受験者分布を計算しています。
まずは男子です。計算すると、こうなります。

慶應義塾と早稲田実業が同じ2/10の入試で重複しており、最大受験数は4校です。模試の持ち偏差値が52の場合、4校受験して少なくとも1校に合格できる可能性は、2/10に慶應受験なら58%、早稲田受験なら53%となりました。持ち偏差値53なら65%と61%です。
続いて女子です。

女子は早慶附属の受験機会が激減し、最大で2校となります。早稲田本庄+慶應女子か早稲田本庄+早稲田実業の2パターンです。それぞれでのパターンで、2校受験して少なくとも1校に合格できる可能性は、持ち偏差値52の受験生では、前者で22%、後者で28%となりました。持ち偏差値53なら、27%と34%です。
これらのことから、先に引用した本で記載されている「早慶附属高校合格の下限は駿台模試52〜53の受験生」は、男子では十分にあり得る話(52〜65%)であり、信憑性がかなり高いことがわかります。一方で、女子ではかなり厳しい話(22〜34%)であると考えられます。
6. 最後に
合否判定の分布モデルと入試本番のテスト偏差値の変動モデルは概ね整合する前提で、模試の持ち偏差値ごとの志望校(A判定偏差値○)の高校の合格可能性の算定をしてみました。多少のギャップはありますが、この業界の有識者の実体験とも概ね合致する結果と言えるので、まあいい感じのモデルではないか、という印象です。
そうなると、入試本番のテスト偏差値の変動モデルの正規分布(σ:7.8)が、試験ごとの短期的な変動(σ6.1)とギャップが出ていることに興味が移ります。このギャップは、模試から本番までの学力の増減です。この関係を分析すれば、入試本番の合格には、本番の調子と模試からの学力の増減のどちらが大きく影響するのかがわかるはずです。
次回はこの分析をしてみます。
