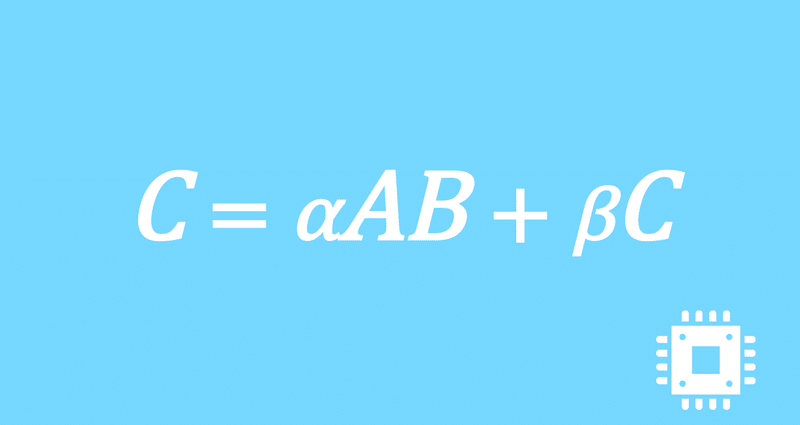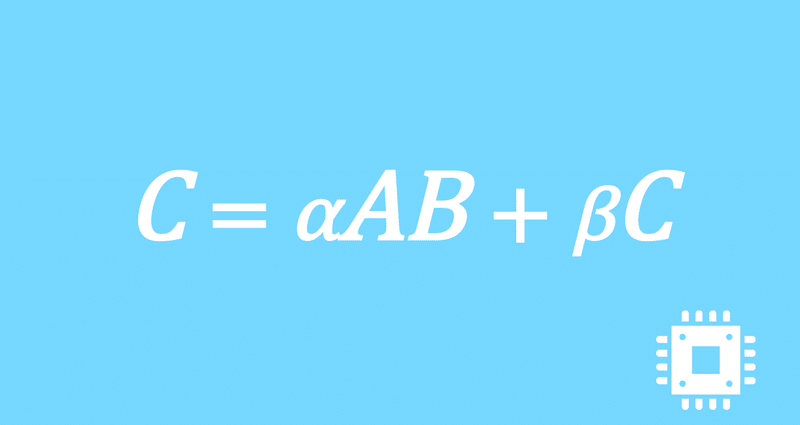マガジンのカバー画像

行列積計算を高速化してみた

30
本
数値計算ライブラリBLASに含まれる行列積ルーチンDGEMMを高速化していく手順を記した記事「行列積計算を高速化してみる」の章ごとに分割した記事をまとめたマガジンです。元の記事は…
運営しているクリエイター
やまもと

#キャッシュブロッキング

はじめに｜行列積高速化#0

以前書いた行列計算DGEMMを高速化する記事が、あまりに長すぎた（20万文字以上）ので、記事あたり１万字以内を目安に、章ごとに記事を分割することにしました。 元の記事が有料記事のため、高速化の重要なカギになる章は有料にさせていただいています。全記事をご購入いただくと1000円になります。元の記事は560円ですので、全ての章を読むなら元の記事の方が割安になっています。一部の章は元の記事で有料部分に含まれていましたが、分割したので無料でもお読みいただけるようになりました。 元

やまもと

ブロッキングサイズの改良｜行列積高速化#26

当初の設計（下記の記事）では、I,J,Kループのキャッシュブロッキングサイズは、キャッシュメモリの容量に収まるように決めました。 しかし、L1キャッシュブロッキングの有無がカーネル関数の性能を左右していたため、性能実測しながらL1~L3のブロッキングサイズを変更することにしました。前回の記事のカーネル関数の性能は、ブロッキングサイズ改良後の測定値になります。 改良したブロッキングサイズ当初の設計では、キャッシュメモリのブロッキングサイズを下記のように設定していました。

やまもと

計算ブロックの順序最適化｜行列積高速化#12

この記事は、以下の記事を分割したものです。 ［元の記事］行列積計算を高速化してみる 一括で読みたい場合は、元の記事をご覧ください。 前節で行列Aのブロック単位のコピー回数を削減しましたが、計算順序を工夫することによって、さらに削減することができます。 12-1. 計算順序の再設計３x３ブロックを例にすると、現在のプログラムでは、下図のようにコピーを行っています。 黄色いマスが計算に使用しているブロックで、数字はコピーの順番を表しています。数字のない黄色いブロックは、コピ

¥100
やまもと

キャッシュブロッキング｜行列積高速化#5

この記事は、以下の記事を分割したものです。 ［元の記事］行列積計算を高速化してみる 一括で読みたい場合は、元の記事をご覧ください。 上記で、メモリアクセスパターンの違いによって、明らかに計算速度の違いが見られました。これは、ストライドアクセスだとCPUが読み込んだキャッシュラインの一部しか利用せず、キャッシュメモリの利用効率が著しく低下しているためです。 そこで、まずキャッシュメモリの利用効率を向上することを目指します。そのためには、利用するデータ量を制限し、データの再利

¥100
やまもと