
【数理的溢れ話2パス目】主観的計量の対数性、あるいは「愛(i)が効用を回す」?
以下の投稿の以下の脱線気味の注釈が全体の可読性を落としているので切り離す事に決めました。以降もそういう事態に対応する為の新シリーズです。
②偏回帰係数
②偏回帰係数$${(a_1,a_2,…,a_n),-∞≦a_n≦+∞}$$を明かにする為に、目的変数Pを確率からオッズ比$${y=log(\frac{P}{1-P}),-∞≦y≦+∞}$$に変換し(ロジット変換)重回帰分析を遂行する。

この辺りの考え方は「情報量と確率の関係」を把握する際にも登場する。
さらには「(差異が検知可能な)驚きの量(等高線)が対数的に推移する」なる認識自体は19世紀における「実験生理心理学の基底」ヴェーバー‐フェヒナーの法則にまで遡り、それが最も厳密な形で確認されるのは「音楽における音の高低」認識の世界である。


お気づきになられたろうか? 計算式こそ全く別物だが、数聖ガウスは天体観測上の誤差について「大きな外れ値ほど出現率が低くなる」と想定して誤差関数(ERF=ERror Function)を設定。それ自体はフーリエが発見した「1点に加えられた熱が時間推移によって伝導していく状態方程式」と密接な関係を有する物理量だが、実際に誤差の予測に有効であり正規分布概念、すなわち推測統計概念の代表的基底となった。
$$
erf(x)=\frac{2}{\sqrt{π}}\int_0^xe^{-x^2}
$$

経済学の世界にも「限界効用の逓減」なる類似概念が存在。この様な「シグモイド曲線を使った閾値による二クラス分類」概念の汎用性こそが機械学習理論の可能性の広さであり、かつ気をつけねばならない要所となってくる訳である。
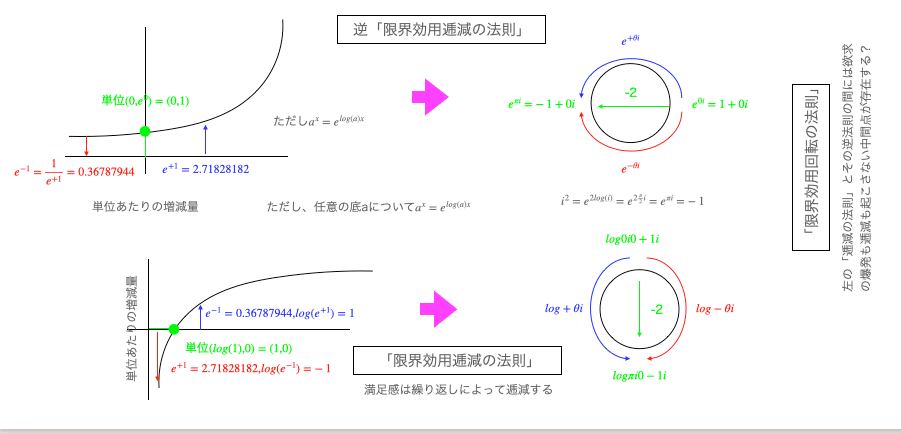
ここで興味深いのは、ここでいう「限界効用の逓減」の推移を対数的でなく円軌道で捉えようとする向きが存在する事。
参照元

「効用=消費財および用益が消費者に与える主観的満足度」とした場合の限界効用の定義は「消費量が1単位増大するのに伴って増大する満足感の総量」というもの。すなわち「複利計算方式=ネイピア数(2.7182818…)を底とする自然指数関数$${y=e^x}$$や自然対数関数$${y=log(x)}$$と底の変換公式$${a^x=e^{xlog(a)}}$$の組み合わせによって任意の推移過程全部が表せる」なる前提に立って水平軸に均等尺、垂直方向に対数尺を置いたグラフで全体像を表す事が多い訳だが…
ここでもし「欲望」と「充足」を単なる「連続する同一数直線上で打ち消し合う相反ベクトル」として捉えず、「閾値=そこで傾きが1となる隠れた乗法単位元$${e^0=1}$$を中点とする直行座標系」を仮定し、限界効用の定義も「絶対値1を変えないまま欲望軸x上における1単位の増減が満足軸yの1単位の増減に回転運動的に推移する過程の欲望軸からの観測結果」と書き換えたらどうなるだろう?

そう、この「それまで好きでたまらなかったものが、欲しいだけ手に入る様になったかえって嫌いになってしまう事もある」現象の説明に便利そうな「拡張」限界効用定義は、まさしくCosineの定義そのものであり、確かに全体としてオイラーの公式$${e^{θi}=cos(θ)+sin(θ)i}$$によって説明される極座標系として表されるのである。
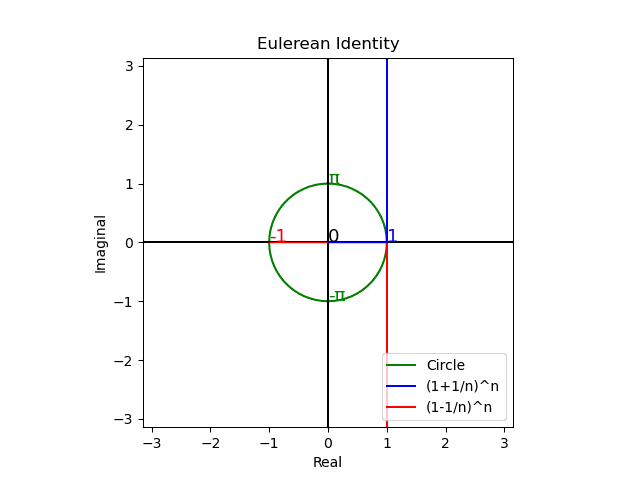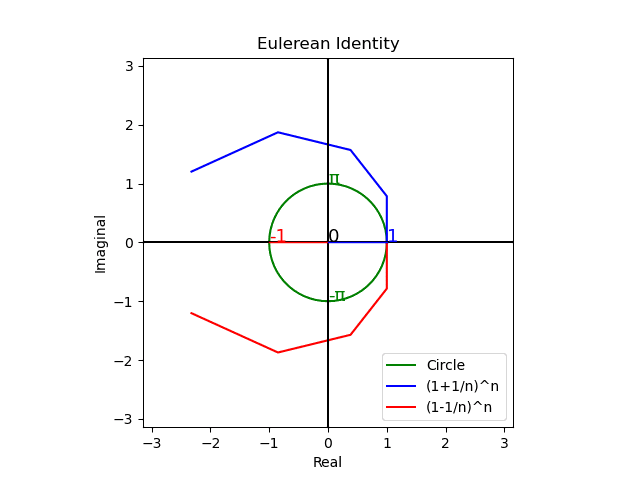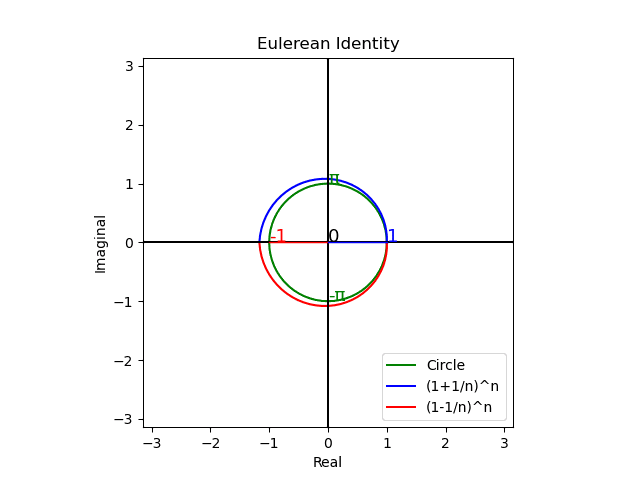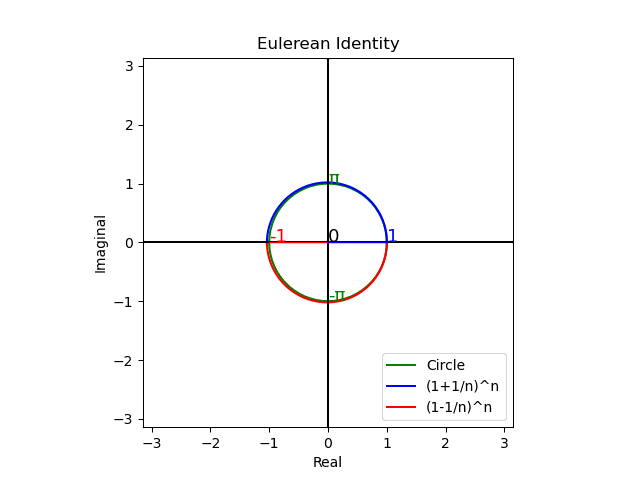
以下の投稿で用いた様に「領主と良民(統治関係)」「夫と妻(夫婦関係)」の様な二項関係の分析で使える考え方ですね。
まさしく文字通り「愛(i)が効用を回す」世界。そんな感じで以下続報…
