
【数理的溢れ話23パス目】天人相関説に復興の兆し?
古代から中世にかけては世界中において「マクロコスモスとミクロコスモスが何かしらの形で連続している」と考える天人相関説が人気でした。
一方、近年の科学実証主義の世界においては「マクロコスモス(事象全体)とミクロコスモス(泡沫事象)の統計学的相互関係」が大きな話題となりつつあります。今回はこの辺りの話を巡る数理を探っていきたいと思います。
無限連続実数直線からリーマン球面へ
我々が概ね「数」と捉えるのは「一次元の無限連続実数直線ℓ(-∞≦ℓ≦+∞)」だったりする訳ですが、実はその次元だけでは厳密な定義が不可能だったりするのです。

例えばガウスは無限遠(Infinity)を「観測原点Oから任意の無限連続実数直線ℓに下ろされた垂線が全て平行(すなわち無限連続実数直線とは直交し)かつ等距離となる場合の観測原点Oと無限連続実数直線ℓの距離」と規定しました。

最後に「水平面が極座標系の円筒座標系」概念が登場するが、これは無限連続実数直線ℓを定義するまた別のアプローチ「N次元空間において2点が与えられ、その距離から相加平均と偏差を求めてその値をそれぞれ+1と-1と置いた場合の相乗平均$${\sqrt{-1}}$$を求める」とも縁深い。要するにある数xの値が担保されるには乗法元1が掛けられている必要があり、その事を「x+1i」なる表現で明示的に示そうという魂胆なのである。

なおガウスが定義した無限遠の特徴は、円状座標系における中心と円弧、球面座標系における対蹠と赤道線の関係と重なってきます。
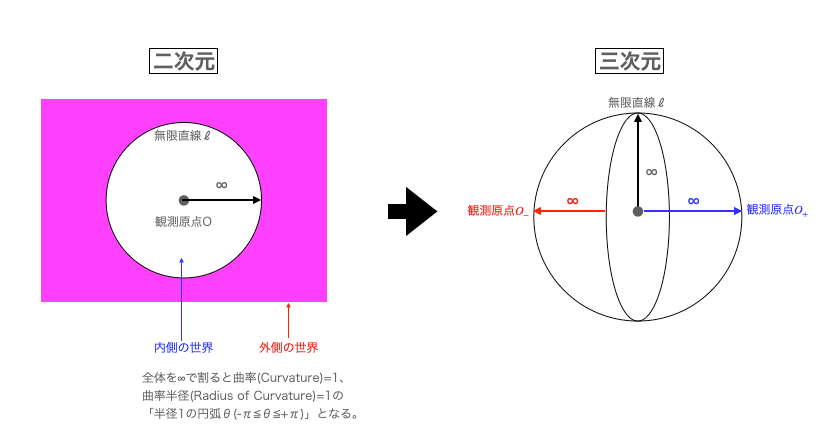
そこで今度は無限連続実数直線ℓ(-∞≦ℓ≦+∞,曲率=0,曲率半径=∞)を半径1の円弧θ(-π≦θ≦+π,曲率=曲率半径=1)にどうやって射影するかという話が浮上してくる訳ですが、まさにこの目的に適うのがタンジェント関数θ(Tangent,$${(-\frac{π}{2}≦θ≦+\frac{π}{2})}$$)およびその逆関数たるアークタンジェント関数ℓ(Arctangent=$${tan^{-1}}$$,-∞≦ℓ≦∞)という次第。
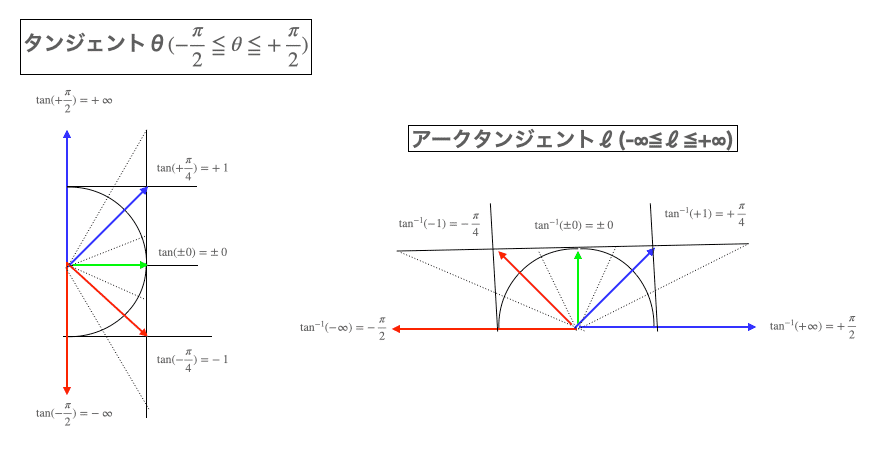
ここに虚数$${-1=i^2=i^{1-\cos(θ)}}$$の概念を導入するといわゆるリーマン球面、すなわち「半径1の赤道線を中心に片方の対蹠が0、もう一方の対蹠が∞となる球面座標系」が現れます。まさしくミクロコスモス=泡沫事象とマクロコスモス=事象全体が対峙する図式の復活…

逆をいえば「無限連続実数直線ℓ(-∞≦ℓ≦+∞)の両端が垂直方向2で交わる半径1の円座標系において、その角度は$${2tan^{-1}ℓ}$$で求められる」という事ですね。この時の分割、正確には1と∞-1の対比なのですが「∞-a=∞」が無限遠点の定義なので「1と∞の分割」と単純化される訳です。
事象全体に対する泡沫事象のあるべき最大サイズとは?
とりあえずこうして全ての出発点となる「ミクロコスモス(泡沫事象)とマクロコスモス(事象全体)の峻別」は定義されるのです。

観測原点Oから任意の無限連続実数直線ℓに下ろされた垂線が全て平行(すなわち無限連続実数直線とは直交し)かつ等距離となる場合の観測原点Oと無限連続実数直線ℓの距離
この辺りの考え方を脳内でうまく扱えない人が地球平面説に走ったりするという話ですね。
∞-a=∞(aは数えられる有限数)
この定義、一般的な人間の感覚だとどの時点から適用可能となるのでしょうか? 昨年の私はとりあえず古代バビロニア文明にまで遡る60進法をその基準に選んでみた次第。
1分(60秒)に対する1秒
1時間(60分)に対する1分
1日(24時間)対する24分
地球全体の大きさに対する$${\frac{1}{60}}$$の距離

ちなみに特定の気体や液体を構成する粒子の運動(微視的事象)が全体の温度や圧力(巨視的事象)を決定すると考える統計力学(Statistical Mechanics)の観測単位はアボガドロ定数=$${10^{23}}$$…
一方、「言葉をベクトル化して、その頻度分布と条件付同時出現分布から分布意味論的座標系を構築する」自然言語処理(NLP=Natural Language Processing)一種として出発した大規模言語モデル(LLM=Large Language Model)の雄transformerアルゴリズム。不思議にもこのモデルはセル数が$${10^{28}}$$を超えたあたりから劇的にパフォーマンスを伸ばした事で知られています。
それぞれの「泡沫事象の切り捨て範囲」には相応の意味があるはずですが、現状では分からない事だらけ。この世界を解析し尽くすのが如何に不可能な事業であるか改めて思い知らされる展開に…
コーシー分布(Cauchy distribution)への拡張。
かかる「ミクロコスモス(泡沫事象)dとマクロコスモス(事象全体)ℓが一対一で対峙する可換空間」においては、大数の法則も中央極限定理も通用しない。まさしくウシャニパッド哲学における「梵天一如」認識状態そのもの。
数え上げ可能な数aについて、それを超越した無限遠♾️在り方を「♾️±a=♾️」なる表現で規約する。この時、自明の場合としてマクロコスモス(事象全体)ℓは「無限遠点で無限連続実数直線の両端±♾️が交わる範囲全て」、ミクロコスモス(泡沫事象)dは「マクロコスモス(事象全体)ℓを無限個に分割した単位1(∞×1=1×∞の可換空間)」と規定される。
無限連続実数直線の両端±♾️から数え上げ可能な数a以上離れたミクロコスモス(泡沫事象)dは(♾️±a=♾️の定義が適用される為)、平行移動距離がα未満である限りその計算上の位置を変えない。従って平均の概念を持たず、かつ平均が存在しない以上分散の概念もまた備えない。
加法系における「平均も分散も存在しない」情景。

その指数写像を取った乗法系における「添字の加減算が無効となる」情景。

逆をいえば、かかる条件下において任意のミクロコスモス(泡沫事象)dがマクロコスモス(事象全体)ℓの何処にあるか明らかにする計算方法もまた存在しません。まさしくこの座標系には同一円弧上に実元として(0,±1(d),±∞=$${\tilde{∞}}$$(ℓ))が存在するのみ。もちろんそこで加減乗除の四則演算は成立しますが、上掲の実元影響を与えない(届かない)という意味合いにおいてかかる計算結果はある種の虚元として存在するに過ぎないとも。
実際に体験可能な範囲で探すなら「目の前の水平線や地平線に幾ら近付こうとしても、幾ら離れようとしても距離感が全然変わらない」状況に対応するといえるかもしれない。
もちろん地球の表面上においては「1日に移動可能な距離上限(1340km)を同一方向に60回繰り返すと同じ場所に戻ってくる(可能性がある)」みたいな例外展開も一応は想定可能だが、誤差などの累積もあって個人がそう簡単に思いつきで実践可能な範疇になく、まさにその辺りの認識上の限界が無限遠概念への自然な形での連続に結びついていく。
コーシー分布(Cauchy distribution)概念の導入
上掲の奇妙な座標系をそのまま「水平範囲+∞からー∞、垂直範囲0から1」に正規化(normalizing)するとコーシー分布(Cauchy distribution)となります。
①まず、水平方向には+∞からー∞、垂直方向には$${-\frac{π}{2}}$$から$${+\frac{π}{2}}$$にかけて展開するアークタンジェント(Arctangent)$${\tan^{-1}(ℓ)(-∞≦ℓ≦+∞)=θ(-\frac{π}{2}≦ℓ≦+\frac{π}{2})}$$を用意する。
$$
\tan^{-1}(ℓ)(-∞≦ℓ≦+∞)=θ(-\frac{π}{2}≦ℓ≦+\frac{π}{2})
$$
②その垂直展開を(πで割って$${\frac{1}{2}}$$を足す事で)0から1の範囲に正規化。これが標準コーシー分布(standard Cauchy distribution)の累計度数関数(CDF=Cumulative Distribution Function )F(x;0,1)となる。
$$
F(x;0,1)=\frac{1}{π}tan^{-1}(x)+\frac{1}{2}
$$
③さらにこの累計度数関数を微分して標準コーシー分布の確率密度関数(PDF=Probability Density Function)f(x;0,1)を得る。$${(\tan^{-1}(x))^{'}=\frac{1}{1+x^2}}$$なので、これを使う。
$$
F(x;0,1)^{'}=f(x;0,1)=\frac{1}{π(1+x^2)}
$$
④使い勝手を増す為にパラメーターとして分布の最頻値=中央値(コーシー主値)を与える位置母数(Location parameter,標準コーシー分布では0)$${x_0}$$と半値半幅(リーマン球面でいう半径)を与える尺度母数(Scale parameter)γを定める。
コーシー分布(累積分布関数)
$$
F(x;x_0,γ)=\frac{1}{π}tan^{-1}(\frac{x-x_0}{γ})+\frac{1}{2}
$$
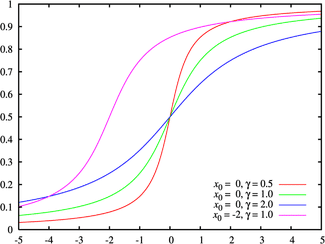
コーシー分布(確率密度関数)
$$
f(x;x_0,γ)=\frac{1}{πγ[1+(\frac{x-x_0}{γ})^2]}=\frac{1}{π}\frac{γ}{(x-x_0)^2+γ^2}
$$

この分布は主として比較的裾野の薄い正規分布(Normal distribution)より外れ値を強く意識しないといけない状況、例えば金融データや原子核物理学および素粒子物理学におけるエネルギー共鳴の記述などに使われます。

ブラックスワン概念の導入
かかる「梵天一如」構造は、いわゆる「ブラックスワン現象」まで扱えるのが魅力ですが、それはもう確率計算可能な領域ではありません。
「ベイズ更新」の概念を用いた場合も同様。条件が総入れ替えとなるので連続的計算が不可能となる訳です。
最近でいうとまさしくiPhoneが登場してノキアのSymbian OSやDOCOMOのiModeやAuのEzwebが一瞬にして歴史の掃き溜め送りとなる一方、GoogleのAndroidの急追を受けてスマートフォン市場の独占自体には失敗した展開。
童話「シンデレラ」において、かつて王子様の伴侶を巡るどんな政略結婚案が画策されていたにせよ、それは「ガラスの靴の美女」の登場によって最初からなかったものとされてしまった。
そして物語中においては自明の場合として「ガラスの靴の美女=シンデレラ」の構図が承認されてハッピーエンドに終わったが、現実の世界ではまた異なった結末を迎える事もある。
たかがミクロコスモス(泡沫事象)、されどミクロコスモス(泡沫事象)という感じですね。そんな感じで以下続報。
