
【数学的溢れ話13パス目】ガウス「ムッツリスケベは濡れ衣」補筆
これまで以下の様な投稿を重ねてきた訳ですが…
これらの考察の数理的延長線上で執筆したつもりの以下のQiitaの投稿で様相が一変。「オイラーやガウスの様な天体運動や自然現象の様な絶対不動の物理学的存在の観測結果から誤差を除くのが統計の主な役割だった時代の大数学者」を長寿のエルフや魔族、「生物や人間の集団の様なあやふやな対象に統計学的数理を求める様になった時代の統計屋や数学屋」を短命な人類に擬えた割とハード目な歴史観を展開する事になったのです。
まぁ普通に考えて「葬送のフリーレン」の以下の展開に引き摺られた形。その雰囲気が最もトールキン「指輪物語」の悲観的歴史観に近付くくだりですが原典とは「英雄の時代が終わる」事への悼み方がまた異なるという…





まぁ現実の「大数学者の時代」にはガウスがアーベルを、コーシーがガロアを冷遇して早逝させたりと暗黒面があったし、産業革命上の要請から始まった統計革命は彼らの存在感をその数学的功績を残してたちまち過去のものとしてしまったのでした。
とはいえ現実の歴史は物語の様に一筋縄ではいきません。「生物や人間の集団の様なあやふやな対象に統計学的数理を求める様になった時代」が最後の歴史となるとは限らず、実際「$${10^{23}}$$の粒子の運動を統計的に扱う」統計力学の延長線上に現れた情報理論の延長線上に「分布意味論的広がりが$${10^{28}}$$を超えた辺りから劇的にパフォーマンスを向上させる」Transformer系機械学習アルゴリズムが姿を表したりしている次第。
ここで興味深いのがノーバート・ウィーナー「サイバネティクス(1948年初版、1961年増補)」に時代において既に情報理論側から「生物や人間の集団の様なあやふやな対象に統計学的数理を求める様になった展開」に疑問が呈されていて、その予言が実現しつつある様にも見える事。例えば以下のトピックについてですが、どう調べても同じ結論に至るのでChatGPTの優等生的まとめを掲示しておきます。
頻度主義とベイズ主義は、統計学や確率論における異なるアプローチです。
頻度主義(頻度確率論):
頻度主義は、確率を「事象が起こる頻度」として捉えます。つまり、確率は過去の観測から導かれるものであり、事象が発生する回数の極限として定義されます。
例えば、コイン投げの場合、表が出る確率は実際に多数回の試行を行い、表が出る回数を全試行回数で割ることで推定します。
頻度主義では、確率は客観的であり、客観的なデータの解釈に基づいて推論を行います。
ベイズ主義(ベイズ確率論):
ベイズ主義は、確率を「信念の度合い」として捉えます。つまり、確率は不確実性や信念の表現であり、新しい情報が得られるたびに更新されます。
ベイズ主義では、事前の信念(事前確率)をもとに新しいデータを考慮し、事後の信念(事後確率)を更新します。これはベイズの定理に基づいています。
例えば、コイン投げの場合、表が出る確率に対する信念を持ち、コインを投げる度に新しいデータを使ってこの信念を更新します。
ベイズ主義では、確率は主観的であり、事前の信念の違いによって異なる結果が導かれることがあります。
簡潔に言えば、頻度主義はデータに基づいて確率を評価し、モデルを構築しますが、ベイズ主義は事前の信念を取り入れてデータと組み合わせて確率を更新し、信念を修正します。
ただChatGPT、自らが情報理論の落とし子なので、一般には「まだ証明されてない」と考えられてる「エルゴート仮説」についてこんな答えを返してきたりします。
エルゴード仮説は、確率過程の理論において重要な概念です。特にマルコフ連鎖の理論に関連しています。
エルゴード仮説は、マルコフ連鎖が一定の条件を満たす場合に、その連鎖がある種の平衡状態に収束するという仮説です。具体的には、以下のような条件が含まれます:
非周期性(Aperiodicity): マルコフ連鎖の状態間遷移グラフにおいて、任意の状態からその状態に戻るまでの周期が一定でないことを意味します。つまり、ある状態から出発して、任意の時間後に同じ状態に戻る確率が0ではないことです。
正則性(Irreducibility): 任意の状態から他のすべての状態へ到達できることを意味します。つまり、どの状態からでも有限ステップで他のすべての状態に到達できることです。
再帰性(Recurrence): ある状態から出発して同じ状態に戻る確率が1であることを意味します。つまり、ある状態が再帰的である場合、その状態に戻ることが確実です。
エルゴード仮説が成り立つ場合、マルコフ連鎖は長期的に平衡状態に収束し、その平衡状態での分布は一定となります。これは、確率的なシステムの挙動を理解する上で重要な概念であり、多くの応用があります。例えば、マルコフ連鎖モンテカルロ法(MCMC)などの統計的手法や、マルコフ連鎖の安定性や収束速度を評価するための手法などにおいて使用されます。
実際マルコフ連鎖モンテカルロ法(MCMC)で収束しないパターンが…
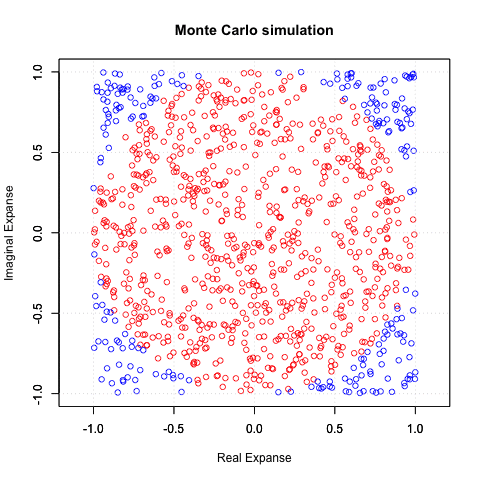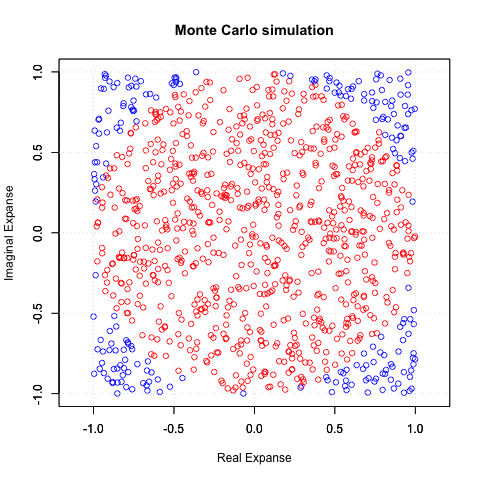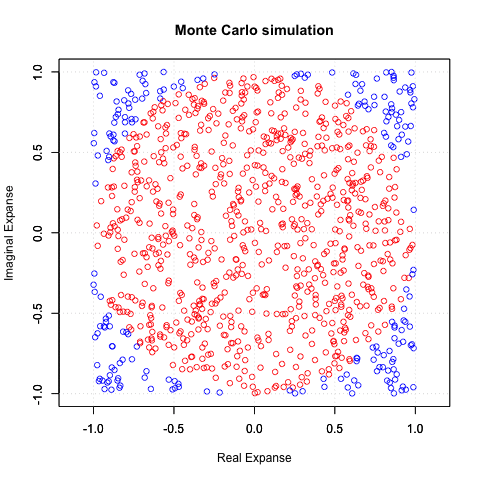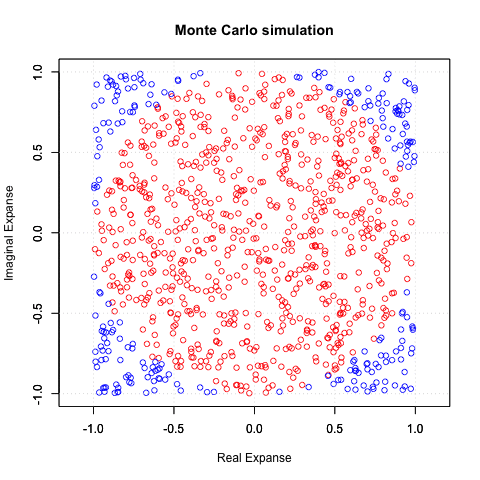
「最大の敵」によりによって「コーシー分布」と大数学者時代のラスボス級の名前がついていたりします。見た目は正規分布に近いのですがとにかく収束しない…
$$
f(x)=\frac{1}{π(x^2+1)}(-∞≦x≦+∞)
$$
こうした全体像を俯瞰すると、当時の大数学者が現代社会に甦っても必ずしも人類側の味方にはなってくれない気がします。そう「転生」といっても「異世界転生」の方でなく「魔界転生」の方って感じ…
最小2乗法から最小N乗法へ
一方、最小2乗法を巡る議論は大体収束したのでここにまとめておきます。
そもそもこの議論の発端はラプラスによる「最小一乗法(1799年)」の発表。詳細は不明ながら「偏差の総計が0となる問題」を絶対値を取る事で解消する技法と推測される。
これに対してガウスが「より優れた理論」として最小二乗法をまとめる(1809年と1823年)の論文。この記述には当然の様に「最小二乗法の最大の泣きどころたる外れ値を除去する」誤差関数への言及も含まれていた。
ここまでの議論は天体観測や地球測量といった物理的存在の観測誤差除去の話だったので概ね平均値と中央値と最頻値が一致したが、産業革命導入などを契機に統計学が生物や人間の集団の様な「あやふやな存在」も観測対象にする様になると貧富格差分布などを扱う為に「最小絶対値法」が復活。今日では「ロバスト回帰」などと呼ばれている。
まぁ最小二乗法、こういう「自然現象の観察においては想定する必要がなかった」状況に極めて弱いのです。
中央値だと18歳前後だが、平均値だと300歳を超える女子会 pic.twitter.com/hKxTmnMixJ
— 妥狂帝リコリス (@Licorice_DAKY0U) March 28, 2024
そういう状況で役立つのが「(論破された筈の)ラプラスの亡霊」ロバスト回帰という訳です。初見なので私も全然内容を理解しておりませんが、実用に到達してるだけあって相応に練り上げられた理論に見えます。
驚いたのが機械学習理論の分野ではさらに「最小0乗法」と「最小4乗法」が加えられ「最小N乗法」なるジャンルが構成されたという話…
まぁ「最小4乗法」については最小2乗法に増して外れ値の影響が大きくなる上、曲線に対する曲線のフィッティングになるので「鰻の掴み取り大会」の如き有様となり実用化には程遠い模様。一方「最小0乗法」というと一見偏差を0乗しても1がズラリと並ぶばかりで分布も収束もへったくれもない様に思えますが、そこを「ただの0」でなく「極限としての0($${\lim_{a→0}\lim_{b→0}a^b}$$)」について考える方向での試行錯誤が行われているとか。というのも平均値が「最小二乗法」に、中央値が「最小一乗法(ロバスト回帰)」に紐付く様に「最小0乗法」は(上掲の「その広がりが$${10^{28}}$$をを超えてからが本番の分布意味論空間」において唯一通用する尺度たる)最頻値と紐付いているからで、ひょっとしたらこの分野からまた新しい考え方が台頭してくるかもしれません。
こうして全体像を俯瞰してみると、少なくともこの範囲についてはガウスが「当時の世相に配慮した隠し事」をしてない事は明らか。なので、とりあえず切り離しておく事にしたという次第…
ガウス分布の名付け親はガウスじゃない?
そもそもここで「ガウス分布の名付け親はガウスじゃない」問題が表面化してきます。誰もがあまり語りたがらない統計学の暗黒史…
この話に踏み込むとさらに長くなってしまうので以下続報…
