
相関分析 「風が吹けば桶屋は儲かるのか?」を解明する方法
今回は複数のデータの関係性を明らかにする「相関分析」についてです。
さて、タイトルの「風が吹けば桶屋は儲かるです」が、ご存知の通りことわざで、ある事象が一見まったく関係がないようなことに影響を及ぼすことのたとえです。英語圏でもバタフライ・エフェクトという言葉があって「ブラジルの一匹の蝶がテキサスで竜巻を越すことを」検証したという話からきています。
自社の商品の売上や来店数に、何らかのその他の要因(例えば、気温など)と相関関係があることが分かれば、売上予測やそれにもとづく仕入計画なども立てやすくなりますので戦略の立案などに役立つデータとなります。
では、どうやって要因間の相関関係を見つけるか、ですが、まず2つの要因をそれぞれ縦軸と横軸にとって収集したデータをプロットし散布図を作ったとします。
以下の図表が散布図の例となります。
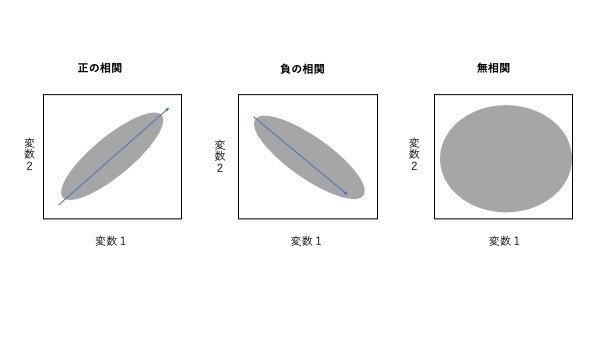
左側の図のようにデータの集まりが何となく右肩上がりになっている場合は、変数1と変数2の間には「正の相関関係」があると考えられます。
相関係数は0<相関係数≦1となります。
右側の図のように右肩下がりの場合、「負の相関関係」があります。
0>相関係数≧-1の範囲となります。
一番、左側のようにデータがばらついている場合は、相関関係がなく無相関となります。
この場合は、相関係数=0です。
相関係数が+1であれば、完全な正の相関で右上に上がる1直線上にデータが全て並ぶことになります。
現実のデータの世界でそのようなことはほぼなく、外れ値を含むデータから相関係数を算出する必要があります。
では、どうやって相関係数を算出するかですが、以下が相関係数を算出する式となります。
相関係数=共分散÷(標準偏差1×標準偏差2)
共分散は、2変数の偏差の積の平均のことです。
エクセルでCOVARIANCE関数を使うとすぐに計算できます。
標準偏差は、平均からのばらつきを平方根で表したものと以前に説明ました。
相関係数もCORREL関数を使うとすぐに計算できます。
まとめ
相関係数の求め方についてでした。相関分析については、次回もう少し掘り下げて検定や擬似相関についてまとめたいと思います。
最後までお読みいただきありがとうございます。
