【人事×Tableau】残業時間を箱ひげグラフで表現する

2024年6月13日 23:09

人事領域の課題をデータドリブンでTableauで解決しようとしています。

今回は、毎月報告する労働時間について箱ひげグラフを作成してみようと思います。

箱ひげグラフとは？

箱ひげグラフ（Box Plot）は、データの分布を視覚的に表現するための統計的なグラフです。
データの分布や偏り、異常値を確認するのに役立ちます。
社員の労働時間は偏差が生じやすいので、これが確認できるとばらつきがわかり、業務負荷が生じている社員の業務を分散したりできます。

箱（Box）：データの第一四分位数（Q1）から第三四分位数（Q3）までの範囲を示します。箱の中の線はデータの中央値（第二四分位数、Q2）を表します。
ひげ（Whiskers）：箱の両端から伸びる線で、通常はデータの最小値と最大値を示します。ただし、ひげの長さはデータの範囲に応じて適切な方法で計算され、異常値（アウトライアー）を除いた範囲を示します。
異常値（Outliers）：箱とひげの範囲外に位置するデータ点を示します。

詳しい説明は後程にして、さっそく作成してみます。
今回も、先日ChatGPTに作成してもらった社員データを用います。

行：時間外労働時間（メジャー：平均を徹底）

と設定し、右側にあるグラフの表示形式を箱ひげグラフを選択します。

列：本部（確認したい項目ごと）
詳細に氏名を入れると完成です！

営業一部を確認します。

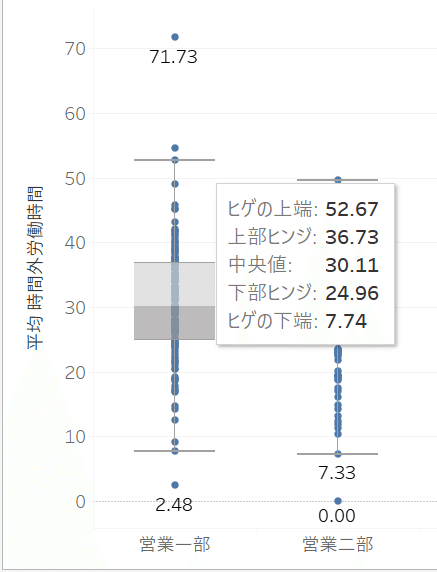
中央値（30.11）：営業一部の時間外労働時間の中央値は30.11時間です。これは、営業一部の社員の50%がこの時間より多く、50%がこの時間より少ないことを意味します。
上部四分位数（Q3: 36.73）：営業一部の時間外労働時間の上位25%の範囲の開始点です。
下部四分位数（Q1: 24.96）：営業一部の時間外労働時間の下位25%の範囲の終了点です。
箱の範囲（24.96〜36.73）：この範囲には営業一部の時間外労働時間の中央50%が含まれます。
ひげの上端（52.67）：営業一部の最大の異常値を除いた範囲内での最大値です。
ひげの下端（7.74）：営業一部の最小の異常値を除いた範囲内での最小値です。
異常値（71.73）：この点は他のデータポイントと比べて極端に大きい異常値です。

マウスを動かすと、↓のように誰なのかもすぐに分かります！

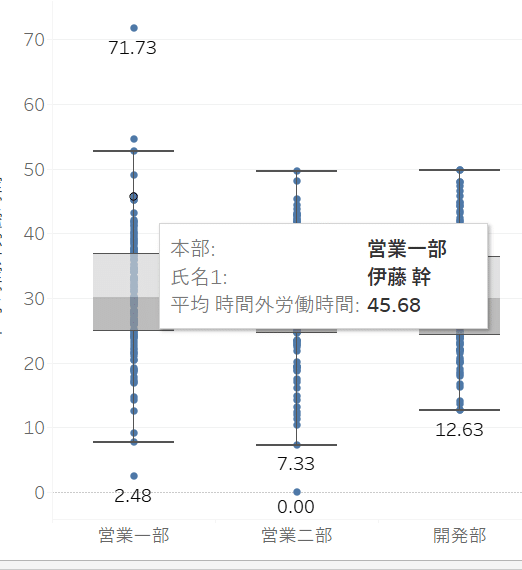
ちなみに、中央値が30なのは、事前にこのサンプルデータを作成した際に平均30時間で！とChatGPTに頼んだからです。
あまり面白いデータにはならなくて悔しいですが、実際に自社のデータで作成してみるとバラバラでした。

中央値（第二四分位数、Q2）：データの中央の値です。全データを小さい順に並べたときに、ちょうど真ん中にくる値です。データの半分がこの値より小さく、もう半分がこの値より大きいです。

例えば、今回のように、社員の労働時間を本部ごとに箱ひげグラフで表示する場合。

これにより、労働時間の偏りや異常を見つけ出し、労働環境の改善や適正な労働時間の管理に役立てることができます。

人事責任者なら、箱グラフ見たいですね。
偏差や異常値は本部によりバラバラです。
人事×Tableauは本当に効果的に人事の分析が出来そうです。