
勉強は思い立ったが吉日〜知識量と学習コストの考察~
――知識量だけが違う同じ能力の2人を比べたとき、新しい知識を学習するときどれくらいの差が生まれるか?
この問題を考えてみようと思います。
「知識量だけが違う同じ能力の2人なんて居るの?」と思うかも知れませんが、なんのことはなくて、今からちょっとだけ勉強して寝て起きた明日の自分と、今から何もせず過ごして寝て起きた明日の自分を比べれば、だいたいこういう状況かと思います。
考えてみた感想としては、勉強は「思い立ったが吉日」です。
▼問題のモデル化
①モデルの提案
定量的に考察してみたいので、以下のようなモデルを考えてみます。
新しい知識を1つ学習するために、
①平均 k 個の前提知識が必要となる。
②各々の前提知識は平均 s ステップ前まで遡る必要がある。

たとえば、「ブロックチェーン」がどんなものか知りたいとしましょう。
「ブロックチェーン」を調べてみると、理解するためには「ハッシュ」だったり「分散ネットワーク」だったりを理解する必要があると分かります。
もちろん、すでに知っている人からすればこれだけで理解できるのですが、「この分野にくわしくない人がバズワードとしての『ブロックチェーン』に興味をもって調べ出した」ような状況を考えてみると、おそらくこんな状況になることが予想されます。
しかも、「ハッシュ」を理解するためには「データ構造」や「関数」など、「分散ネットワーク」を理解するためには「ネットワーク」やその「分散」の意味を理解する必要があります。
このことから、1つの新しい知識を得るために、前提知識を数ステップ遡る必要が生じる場合がよくあります。
このモデルのもと、N個の知識を新たに学習したい場合に「全部でいくつ学習しないといけないか?」を考えていきます。
ここでは、「知識を新たに学習するのに必要な学習の総数」を「学習コスト」と呼ぶことにします。

②「学習コスト」の計算
もう一度「新たに1つ学習」する場合の図を見てみましょう。

総数は以下のように計算できることが分かります。分かりにくい場合は、kとsを2とか3くらいの場合で図を描いてみると理解の助けになるかと思います。

これは1個の場合だったので、N個の場合はこれをN倍してやれば求まります。高校数学で習うΣ(シグマ)という和の記号を使うと、こんな感じでスッキリ書けます。

これは、高校数学で習う「等比級数の和」の公式を使うとすぐに計算できます。すると、求めたい「学習コスト」は次のようになります。

▼具体例を考える
①考えてみる状況の設定
知識量の違うAさんとBさんを考えて、2人の「学習コスト」を比較してみましょう。
AさんはBさんよりも物知りで、Aさんが「1つの知識を新たに学習するのに必要な前提知識」は、Bさんよりも各ステップで平均 k' 個少ないとしましょう。言い換えれば、1つの知識を学習するために、BさんはAさんよりも各ステップで平均 k' 個余分に学習する必要があります。
この設定で、先ほど計算した結果からAさんとBさんそれぞれの「学習コスト」を計算してみましょう。


Bさんの方がAさんよりも「学習コスト」が大きくなると思われるので、「新たにN個学習するとき、BさんはAさんの何倍学習する必要があるか?」を計算してみましょう。
計算してみるとこんな感じです。

kやsが小さい、計算が簡単な場合で具体的に数値を入れて計算してみましょう。
以下では
(k,s)=(1,1)、(2,1)、(2,2)
の場合について計算していきます。
※(k,s)=(0,0)の場合は差は出ない(1になる)ので省きます。
②(k,s)=(1,1)の場合
新たに1つ学習する場合に、平均1ステップ遡って、平均1つ余分に前提知識を学習する必要がある場合です。
この場合に計算すると、以下のようになります。

これがどういうことかというと、AさんがBさんより平均2個多く前提知識を持っているとき、BさんはAさんの2倍学習する必要があります。
③(k,s)=(2,1)の場合
新たに1つ学習する場合に、平均1ステップ遡って、平均2つ余分に前提知識を学習する必要がある場合です。

この場合、AさんがBさんより平均3個多く前提知識を持っているとき、BさんはAさんの2倍学習する必要があります。
④(k,s)=(2,2)の場合
新たに1つ学習する場合に、平均2ステップ遡って、平均2つ余分に前提知識を学習する必要がある場合です。

まだちょっとピンとこないので、k’ が小さい場合で計算してみましょう。
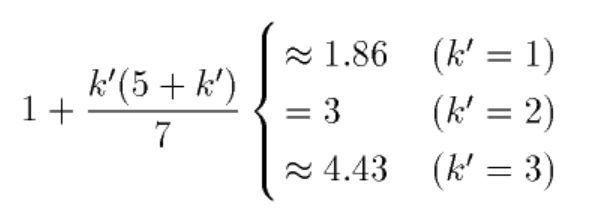
k’は「AさんがBさんより、各ステップで平均k’個多く知っている」ことを表すパラメータです。
つまり、「1学習あたり2ステップ必要で、各ステップでは2つ余分に学習する必要がある場合」にはAさんがBさんよりも各ステップで、
・平均1個物知りだった場合→1.86倍
・平均2個物知りだった場合→3倍
・平均3個物知りだった場合→4.43倍
BさんはAさんよりも余分に学習する必要があります。
▼まとめ
モデル自体やkやsの大きさにもよりますが、たとえばこんな簡単なモデルを考えただけでも、やはり前提知識があることは新たな学習をするとき有利になると思われます。
冒頭にも書いたように、これはAさんとBさんという別人2人というよりも「今から勉強した明日の自分」と「今から勉強しなかった明日の自分」を比べるとより危機感を感じるかも知れません。
「毎日1%改善できると1年後には38倍くらい改善できる」とかこの類の話で、長くやらないほど差が開いてしまいます。
ちょっとした差が複利的に積み重なると大きな差になることを考えると、「勉強してみようかな?」と思い立ったまさにその瞬間始めるくらいが絶好の始めどきなのだと思います。
