
間の数〜授業参観〜
1.はじめに
3年生の2学期の終わりは単元「間の数」を学習する。図に表すことで式を導き出すことができればと思い授業を行った。

いきなりではあるが、この式はどのように考えたか分かるだろうか?
この考え方の正体はこの後授業の内容を説明する中で明らかにしていく。
ここからは授業の具体について書いていく。
2.導入
似た問題を引き出す仕掛け
私は、以前まで本時の問題を提示した後、似た問題を子どもに聞き、既習の問題と本時の問題を同じ構造、似た構造の問題と捉えることができるよう仕掛けてきた。
その意図は、似た問題を引き出すことで、その問題で使ったカードを使って本時の問題も解くことができるのはないかと類推することができると考えたからだ。
しかし、先日の授業公開で教師が問いかけるのではなく、子ども水がが考えだす引き出す仕掛けが欲しいということをアドバイスいただいた。下記の内容↓↓
そのため、授業参観の本時で新たなチャレンジをした。
心理的安全性を高めるために、挑戦が大事とクラスの子たちにも言っているからこそ、私もあえて挑戦した。
仕掛け1.問題提示の工夫
問題場面は教科書同様、
15人が1列に並んでいます。あゆみさんは前から 5番目、ゆうとさんは後ろから4番目です。
で問題を提示した。
本時でも、前回同様、問いかけの文章を工夫し、子供たちが自ら既習とのつながりに気づくことをねらった。本時は、前回の公開授業でもらったアドバイス
答えの出ない問いかけの文章で問題提示を行った。
いただいたアドバイス
答えの出ない問いかけの文章を出したとしても、それは答えが出ないと判断し、正しい問いかけの文を作ることができることも大切
実際のやりとりは以下のように行った。
提示した問題
15人が1列に並んでいます。あゆみさんは前から5番目、ゆうとさんは後ろから4番目です。
実際のやりとり
T:今日ある情報はこれだけだよ。今日のQは、
1列は何メートルですか?です。
C:これは解けないよ!
C:情報はこれだけなんだよね。
C:他にも情報あるの?
T:どうしてそんなこと聞くの?
C:このQの文章では、問題として成立しないから…
T:そうなの?先生が作ったのに?では、解くことができる問題を作ってみよう。
仕掛け2 発問の工夫
子供が問いかけの文章を考えた後、発表させた。
すると
ゆうとさんの前には何人いますか?
あゆみさんの後ろには何人いますか?
2人の間には何人いますか?
この3つの問いかけの文章が表出した。そこで、私は、
みんなにとってどの問題が1番簡単なの?
と問題の難易度を比較する発問をし、
実際に選んだ問題の解決方法を考えることで習ったことがある問題とそうでない問題を区別できるのではないかと考えた。
実際に、子供たちは
あみさんの後ろには何人いますか?
優斗さんの前には何人いますか?
これらが簡単だと発言した。そこでこれらの2問の問題を黒板上で解決していくと、
これ習ったじゃん
と想定通りの声が聞かれた。
このような流れから、本時は、2人の間の数を求める問題について考えようと問いかけの文章とめあてが出来上がった。

1年生の学習と3年せで作ったカードをつなぐ
本時もカード実践で行ったが、子供たちは1年生では、学んだことをカードにはしていない。そのため
この問題ってカードがあるの?
カード作らないとダメかもしれない!
と。はじめはカードを作る方を多くの子は意識していた。
しかし、
コンパスで長さを比べられるという学習をした時も1年生で学んだ、電車いくつ分、鉛筆いくつ分は○がいくつ分で解くことができたでしょ。だから、今回も1年生で学んだことが、もうカードとしてあるんじゃない?
と、授業参観にもかかわらず、勇気を持って発言しだした子がいた。
また、昔の私の発言を思い出し、
先生1年生の学習は4枚のカードがあれば問題解けるって言ってたから、このカードも多分僕たちカード作ってるはずだね
と言い、カードを見返し出した。
この時、子どもたちは、前から何番目、後ろから何番目の1年生の学習なら何のカード作るのかという議論をしながらカードを探している姿があった。
(今回は、どのカードを選んだか見ている参観している先生はいないので、挙手で捉えたカードの選択を以下に載せる)↓↓↓
33人の選択したカード
図にする、絵に置き換える9人
線分図にする4人
まとめて移動5人
数える7人
サクランボ2
思いつかない・考え中6人
3. 問題解決
本時の授業参観は、保護者が全員来ていたため、せっかくなのでと思い、個人思考の時間に移ったときに、
お子さんの前で解決する過程を見守ってあげてください
と言った。
すると、私が机間指導する道が塞がれてしまい、いつもの見取ったことを価値付けたり、考え方を広げたり、考え方のを聞いたりといつもやっていた技がここで繰り出せないことがわかった。
このように状況が変わることで、いつも自分が何をやっていて、その行為にはどんな価値があるのかと言うことを理解できると感じた。
私が見取ることがてきたのは
子供たちは棒人間を描いていたり、丸描いたり、線分図にしたりして図に置き換えて考えている子がいる。ということだけであった。
しかし、子どもたちはいつも通り、友達と考え方を確認したり、他の考え方があるか他者参照をしたりして、
足し算をして引き算をしている子がいる。
引き算をしてまた引き算をしている子がいる。
1つの式で解けるの?
などと、私がいつもやっていることを、子供たちがやりながら、解決方法が多様にあることに気づいていった。
4.共有でまさかの…
解決方法の共有場面に入ると減減法の考え方の
15 − 5 − 4=6 、15 − 5 = 10 10 − 4 = 6の考え方や加減法という15 − (5 +4) =6 、5 +4 = 9 15 − 9 =6の考え方が上がった。ここまでは図と式を関連づけて考えることができた。
その後、
この4つの式に同じ考え方のものはありますか?と問いかけると、
15 − 5 − 4=6と15 − 5 = 10 10 − 4 = 6が同じ考え方であることや、
15 − (5 +4)=6と5 +4 = 9 15 − 9 = 6が同じ考え方であることを捉えることができた。
この時私はいつも通り授業が展開でき、子供たちも図と式を関連付けて考えることができたことで理解も深まり安心していた。
久しぶりに授業で焦り出した
ある男の子が
先生、Sさんの考え方すごく面白いよ
と言った。そこで私は、Sさんの考えを取り上げ、考え方を聞いてみると、15 − 7 − 2 = 6と式を書いた。これに対し、子供たちは
どういうこと?
わからない?
と疑問を訴えていた。それを聞いたとき私も同様に全くわからないと思っていた。
全員の保護者もいる前で子供の解決方法がわからない、さらに、どのように考えたかも全く検討がつかないとなると、さすがに私も焦りを感じた。しかし救いだったのは面白い考えがあるよと言ってくれた子が、
それは式だけではわかりにくいから絵も書いた方が絶対にいいよ
と言ってくれたことで、その子は絵を描きそれによって少しずつ考え方を紐解くことができていった。
謎解きのスタート
はじめにヒントの図をSさんに描いてもらい、みんなでその考え方を紐解いていくことにした。
図をかいたときに、

私は全くわからなかったが、5、6人の子がわかったと言っていた。しかし、保護者の方見ると、頭を傾けわからない様子だった。
思い切って、保護者に
わかった方いらっしゃいますか?
と聞いてみると、保護者もわかった方はゼロだった。つまり教室内の大人は誰も分からない状態であった。そこで
Sさんの考え方を当てられる人?
と言い、リレー形式で説明をしていくことにした。すると、1番初めの子が
7と言うのはと言って、はじめの4人を○で囲み、
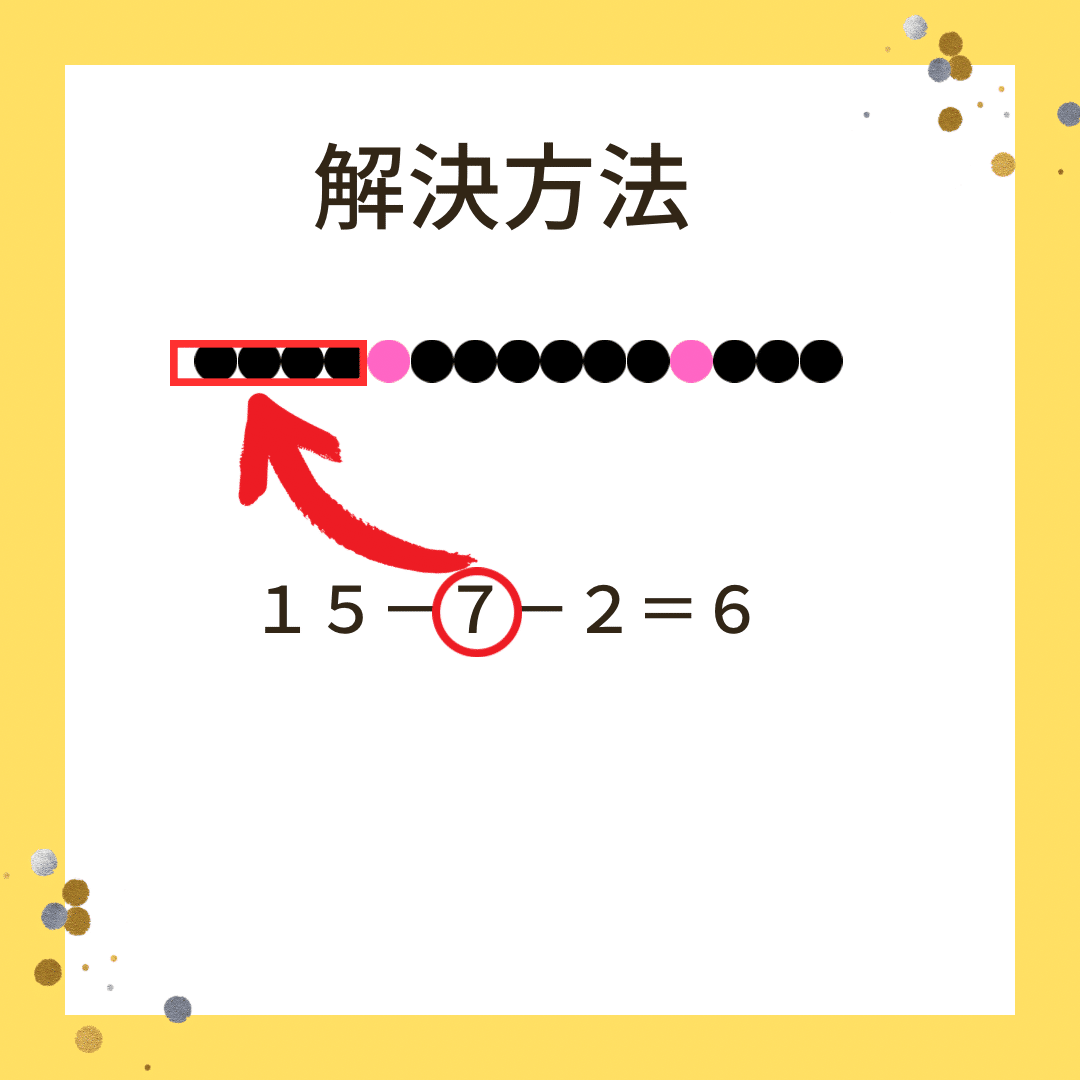
次の子にバトンタッチをした。すると、子供たちの中からわかったという子が増えてきた。保護者も2人わかったと言っていた。しかし、私はまだよくわからなかった。
その後、次の子が後ろの4人に丸を囲んだところで、私もようやくわかった。

クラスの多くの子もそれを機に解決方法を多くの子が理解した様子が見られた。
そして、
− 2の正体はなんですか?
と最後の説明リレーを行った。すると、最後の2人は、ゆうとさんとあゆみさん本人だと言うことがわかり、保護者の方、そして子供たちからもなるほどと感嘆の声が上がった!


5.まとめ
この後保護者の方から
先生、子供がやる気を出すような演技がすごくうまいですね
メジャーな考え方だけでなく、子供の個性のある考え方も取り上げていて、算数楽しかったです
と言われたりした。
今回、これは意図的に取り上げたものでもなかった。また、演技したわけでもなかった。しかし、自分の授業のやり方を保護者の方に授業参観で何度も見ていただいたり、動画で見ていただいたことで、今回の授業をポジティブに受け取ってもらえたのだと思う。
日々の授業をしっかり保護者の方に伝えること。そして子供たちの一人ひとりの考え方に寄り添い、みんなで理解する雰囲気を作ること、そういったことがとても大切だと感じる授業参観であった。
またいつも通り子供のノートを見取ることができない。そんな環境だったからこそ、ノートを見取る大切さや子供に話しかけて考え方の拠り所を探る、普段の行為の価値というものも改めて感じることができた。
そして、何より、大人も夢中になる考えたくなる。そんな授業をすれば子供も楽しむことができるのであろうと考えさせられた学びのある授業となった。
6.授業の終わりに
この授業の後、Sさんの考え方がはじめ全くわからなかったにもかかわらず、一生懸命子供たちが考え発言したこと、わからないことに向き合う姿勢、あきらめない心そういったところも褒め、この授業を価値づけていった。本当に終わってみたら楽しい授業であった。

