
UKD法〜カード実践における発展問題の作り方〜
はじめに
主体的で対話的で深い学びの実現を目指し、最近では個別最適な学び、協働的な学び、複線型授業、自由進度学習、自己調整学習など様々なワードを耳にするようになった。

それと同時にこれらの授業を見る機会も多くなってきました。その中で私は、先生方がたくさんのプリントを準備して授業に臨み、その授業で子供たちが
先生!この問題全部解いたらいいんだよね?
と意欲満々な姿を何度も見ることができた。しかし、この姿を見て、私はこの子供たちは主体的に学んでいるのか?と疑問を持った。

主体的とは?
私は、
先生!この問題全部解いたらいいんだよね?
と言っている児童は主体的ではないと考える。
その理由は、教科書の問題や用意されたプリントを解くことを続けていると、誰かにに何かを準備されないと動けない人、考えられない人になってしまうのではないかと考えたからである。

このような理由から、教科書の問題や用意されたプリントを行うだけでは、主体的に考える児童は育たないと考えた。
提案 問題を自分で発展させる!
そこで私は問題が与えられるという発想から問題を自ら発展させるという発想にマインドチェンジすることが大事ではないかと考えました。
その理由は、問題を解決した後に、自分で別の問題を発見し、働かせてきた見方・考え方が転移できないか考えることで、何かを与えられなくても自分で考えることができるそんな人になることができると考えたからである。

それではどのように問題を発見したり、作ったりしていけば良いのだろうか。
問題の発展のさせ方 手順①構造に着目
例えば、今日の学習で、本時の問題35 +24と練習問題36 +23も行ったとする。この場合、私は本時の問題と練習問題を同じ問題として見ることができないか、問題の類似性に着目させていく。

すると、
繰り上がりのない計算、2桁同士の計算、2項の計算、足し算など、共通点を見出すことができる。

そこで、私は、
今日の考え方を使って解決できるのは、本地の問題や練習問題だけですか
と児童の思考を揺さぶる発問をする。すると、
数を変えたり、数の個数を変えたり、問題場面を変えたりして子供たちは問題を発展させていくことができる。
数を変える、数の個数を変える、場面を変えるという発展させる視点を明確にし、子供たちに提示をするようにしている。

ここで私が大事にしている事は、
問題の類似性を捉えることで、問題の構造を同じと見ることができるようにしていくことである。
問題の発展のさせ方 手順②UKDの視点
問題の構造を捉え、同じと見ることができた後、私はUKD法という視点で発展問題を作ることができるようにしていく。
UKD法とは
UKD法とは、本時の問題や練習問題から
問題のレベルをアップ(上げる)

キープ(変えない)

ダウン(下げる)

の視点から問題を作る方法のことである。
アップ問題を作るときには、Uに丸を打ち、どこを変えて問題レベルをアップしているのか、ポイントをカードに書き記すようにしている。

さらに本時の問題や練習問題で見出した見方・考え方(カード)を作った問題で働かせることができるかを考えているので、問題とセットにして見方・考え方を働かせたことがわかるような解説を作らせ問題と合わせてロイロノートの提出箱に提出させるようにしている。
キープ問題を作るときには、アップ問題とは違い、ポイントを書かなくても良いこととしている。
また、問題を作る事は高度な思考が必要となるため、穴埋め形式での問題づくりのカードも準備をしている。

さらにダウン問題を作るときにはどういう視点で問題レベルを下げたのか、ポイントを記すようにしている。
UKDそれぞれのよさ
UKD法にはそれぞれのよさがある。
アップ問題は、発展的に考え、少し難しい問題を果敢に解くことができる。
キープ問題は、同じレベルの問題を解くことで、技能の定着を図ることができる。
ダウン問題は、過去の学習や下学年の学習と本時の学習を結びつけることができ、統合的に考えることができる。
それぞれ、問題レベルにはよいところがあると考えている。
さらにUKD法は問題を固定的に見ずに、動的に見ると言うことで、問題を発展的に見ることができる事はもちろんのこと、
対話を促す効果もあると考えている。
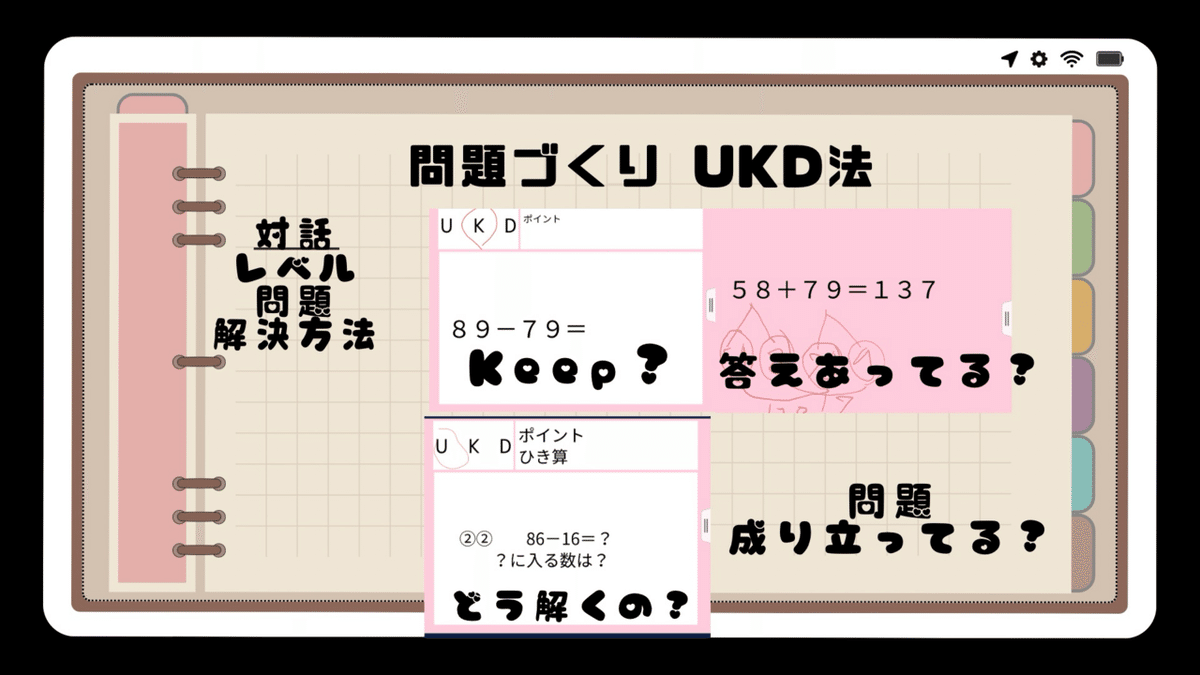
対話を促す効果
UKD法はどのような場面で対話を生み出すことができるかと言うと
問題のレベルは、これでキープなの?
と言う問題のレベルに対する対話であったり
この答えは合ってる?
問題は、成立してる?
と言うような問題に関する対話であったり
この問題難しいけど、どう解くの?
と言う解決方法に関する対話であったり、様々な対話を生み出すことが期待できる。
このように、必要な時に必要な人と関わる非同期コミュニケーションの中で対話を生み出す仕掛けを取り入れていくことで、多様な考え方に触れる楽しさであったり、課題を解決するために必要な人と関わる力というものが伸びてくると思う。

まとめ
私は、このように、UKD法を通して、問題を発展的に見る力や友達と関わる力を大切にして、今後も実践を進めていきたいと考えている。
引用・参考
「生涯にわたって能動的に学び続ける力」を養う教科教育への挑戦
東洋館出版 加固希支男
「自律した学習者を育てる算数授業のカード実践」東洋館出版 樋口万太郎
