
遊び×算数 単元「三角形」
はじめに
3年生の単元「三角形」の第1時で
遊びの中から問題意識を見出し、子供たちが自分で学びを進めることができるような展開を考え、実践を行った。
問題場面
子供たちに
今日はおみくじをやるよ
と以下の紙を青線できり、箱に入れて、おみくじを行った。


そのときに一つだけ約束として、全員引き終わるまでおみくじの中身は見ないこととした。
展開1 大吉とは?
全員おみくじを引き終わり、おみくじの中身を一斉に開けると
大吉だ!
僕は、中吉!
私も中吉!
小吉なんだけど!
私のおみくじには何も書かれていない。
私のおみくじって何吉なの?
どこに大吉とか書いてあるの?
などの声が上がった。子供たちは自分の引いたおみくじを友達に見せてどこに書かれているか、どんなものが大吉なのかみんなで確認をしていた。そんなときに、
僕のは大吉だ!
私も多分大吉!
これ、大吉とか文字なくても自分のおみくじが何か分かるかも!
と直感をもとに発言し始めた子がでてきた。
そこで、子供たちに大吉だと言っていた人のおみくじを見せ

どうして大吉だと思ったの?
と聞き、見方を引き出して行った。
すると、大吉だと予想していた子供は、
だって辺の長さが全部同じものが大吉だもん!
とこたえ、さらに周りの子も
大吉は辺の長さ全部同じだけど、中吉、小吉は辺の長さ全部同じではない!
と論理的な発言し始め、図形の特徴によって大吉などが決まっていることに気付き始めた。
これを機に、大吉とそうでないものの相違点から
辺の長さが全て等しい正三角形のものが大吉
となることを子供たちは気づくことができた。
展開2 中吉、小吉とは?
大吉がどんな三角形のものか、ここまでは子どもたちは直感で捉えていた。その後、中吉と小吉もどんな図形なのかということを、子供たちは考えていった。
ここで、直感だけでは突破できないように
パッと見て二等辺三角形(中吉)に見える一般三角形(小吉)を小吉として入れていたため、

直感だけてなく批判的思考を組み合わせないと考えられないように仕掛けていた。
その結果、
子供たちがコンパスを持ちだしたり、

定規を持ちだしたり、

折りだしたりする行動が見られた。


そこで私は
みんなは折ったりコンパスを使ったり、定規を使ったりしてるけど、どこに注目してるの?また、何をしてるの?
と問い掛けると、
辺の長さに注目して辺の長さを測ってる
と答え、見方・考え方を顕在化することがでてきた。
さらに、折って考えて子は、
長さだけでなく、角に注目して角の大きさが等しい数がおみくじの結果に影響していると思う
と答えた。
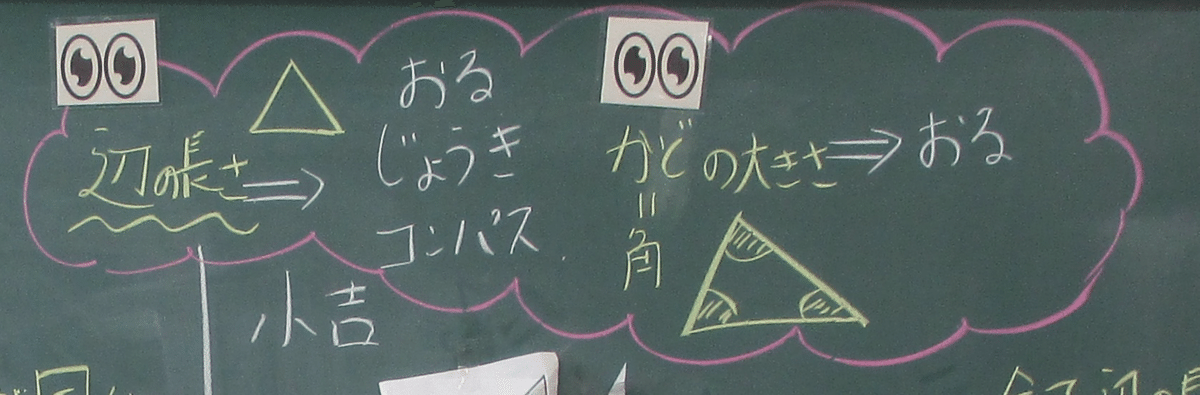
このようにして、
中吉は、2つの辺が等しい三角形、2つの角の大きさが等しい三角形
小吉は、すべての辺の長さがバラバラな三角形、すべての角の大きさがバラバラな三角形
という結論を導き出すことができた。そして最後に自分のひいたおみくじが何吉であったかを考え、黒板にそのおみくじを結ぶことができた。

展開3 次時へ
板書を大吉中吉小吉を分類することができ、子供たちは喜びの声を挙げていたが、そんな時子供たちから僕たちもおみくじ作りたいと言う声が上がった。そのためじじでは、大吉中吉小吉のおみくじを作ることにした。
これ以降は次回のnoteで書いていく。
カード実践の観点から本実践を見ると
本時では、カード選択のときに、
使えるカードがない!
いや、円なら形関係だから使えるかも!
半径に着目する(円の模様作りで作っていたカード)が使えるかな?
でも、半径今回ないよ!
コンパスで長さを比べるとか半径はどこも同じ長さとかもあるけど、使えないか…
というように始めはカードの選択をしようとして苦戦していた。
そして、
使えそうなカードがないので授業の終わりに作ろう
ということが目標となり授業を進めることとなった。
授業進める中で、辺の長さに着目する角の大きさに着目するという言葉が出たとき、ある子が、
円の学習でやった、半径に着目するの進化版じゃん!
進化というより、仲間だよ。というか同じ。円で使った「半径に着目する」が、辺や角になるだけじゃん
さらに「半径に着目する」というものも「辺に着目する」というものも、どちらも図形の線に注目しているってことと同じだよね!
結局はカードは同じだったのか!
と言い出し、
図形を作る線(半径、辺)に注目するというカードを多くの子が作っていた。
半径も辺も図形を作る線で同じと捉えるのか
と子どもの発想に驚かされたと同時に、カードをどんどん抽象化していくところに成長を感じた。
遊びを取り入れる意図を紹介
遊びを取り入れる意図を毎記事ひとつ紹介しようと思う。今回は↓↓

