
4年生「角」の楽しい場面:補助線の引き方と角の見方で広がる算数授業 / 小さな「センス・オブ・ワンダー」
今日は4年生「角」の単元の紹介です。
過去の板書を振り返ると板書の日付が6月になっており、ちょうど今頃が「角」の単元の最中でしょうか。
「角」の単元はどうしても技能(角度を分度器を使って測ることができるか)の習熟が中心になります。分度器の扱い方に慣れる必要もありますし、意外と分度器を使って角度を測ることに困りを感じる子もいます。
技能も高めつつも、友達との関わりの中で「なるほど!」「面白い!」と思える機会を単元の中につくっていきたいです。
「角」の単元で困らないために
まず「角」単元では「角」が理解できないと始まりません。
しかし、私と出会った何人かの子はその角が「何(どこ)を指すのか」がうまくつかめず困っていたことがありました。
4年生の教科書では「角」について、子どものキャラクターが次のように説明しています。
「角の大きさは、辺の開きぐあいで決まるから…」
そして、そのふきだしの下にはいわゆる「角の大きさ」を表した図があります。
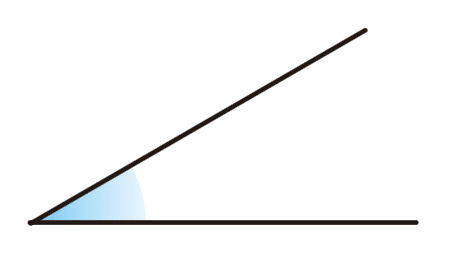
この説明をみたり、聞いたりすることでなんとなく「青の部分なんだな」と理解できると思います。
しかし、その角が「何(どこ)を指すのか」で困っている子は、ここの「開き具合」のイメージをもつことを苦手にしているのです。辺を線ではなく(紙を切って作ったような)「形」として認識しているので、「角の大きさは?」と問われると「角って大きさあるの?角って尖ったところでしょ。」と思ってしまうのです。下の学年で「尖った角」「尖っていない角」といった表現をする子どもたちがいるのは、こういう認識からくるものだと思っています。
この点について、教科書では円の紙を2枚組み合わせて角をつくる活動が組み込まれています。ここで「この辺とこの辺がこれぐらい開いているってことだね!」としっかりと確認をしていく必要があります。
続いて分度器です。分度器は「分度器の中心をどこに当てていいかわからない」という子がいます。頂点が辺と辺が交わったところであり、そこに分度器の中心を重ねることで辺と辺の開き具合が分かるというのはなかなか(はじめは)難しいのです。そうした場合は下の写真のような、辺と角を合わせて認識できるような教具を活用していくと良いです。

https://www.smartschool.jp/products/detail.php?product_id=176000&small_category_id=0&product_code=724661
私の現在の勤務校は、似たようなもので黒板に貼り付き角度を調べられる教具を4年生の全学級整備しています。青の棒がなくて黄色い棒を動かして角の大きさを調べます。(これから紹介する実践は現任校ではありません。)
4時間目:補助線の引き方と角の見方で広がる授業「180度より大きい角度を求める」
「角」の単元では、180度より大きい角度を求める内容が補助線や角の見方を変えることによりある程度広がりをもった授業ができる場面です。

板書を見てもらえば分かるのですが、そこまで難しい内容ではありません。
ここでは「補助線をどうひくか?」「求める角の反対側を角としてみるとどうか?」がポイントとなります。
既習事項として、分度器で測れる180度までの角の大きさを分度器を用いて調べる学習をしてきています。
授業の導入は「次の角の角度を求めましょう」と写真のような角度を提示します。すぐに「え!?」「できない!」と既習と比べて反応する子が出てくるので、話を聞くと「これじゃ180度より大きいから分度器で測れないよ!」と困りが引き出されます。
困っている子どもの話を聞いて、「これ計算すればできるよ!」「(既習の)1直角、2直角…と調べていけばいいんじゃない?」とアイデアが出てくるので(板書左上)、子どもたちに図を渡して調べてもらいます。「先生、線書いていい?」などの質問が出てきたら、詳しく聞くと必ずたし算の式が出てきます。そして、たし算ではなくひき算を書いている子も同時に探しておきます。
交流は子どもに補助線を引かせることから始めました。「この線で何が分かるのかな?」そう問いながら子どもたちに説明してもらうことで、補助線によって角度が分かることがはっきりしてきます。
一方で、もう1つの求める角の反対側を角としてみた子の考えは式から紹介します。「式の360ってどこのことだろう?」と疑問をもたせ、辺が一周回転することで360度開くことのイメージを共有するのです。
子どもの考えを見ていて、考え方によって演算(+、−)が変わるときはチャンスです。特に片方しか考えていない子が多ければ子どもの心は動きます。「なんだこの考え方は!」と思ってもらえるように、少し引っ掛かりがもてるように工夫して提示します。
以上が、180度より大きい角度を求める授業の紹介でした。
「角」の単元で出会った小さな「センス・オブ・ワンダー」
「先生、これね。三角定規は全部180度だと思うの。なんでかな。」
いつも授業にほとんど参加しない女の子がいました。
参加しないというか、人との関わることが苦手で近くの子ともうまく話すことができません。独り言のように話してしまうのです。そのため、授業中は下を向いてノートを書いています。ただ、たくさん書くわけではなく問題を写して答えを書くだけです。だからといって学力が低いわけではなく、テストはほぼ満点でおもしろいタイプ子でした。
「角」の3時間目に三角定規の角の大きさを調べる学習を行った時でした。
子どもたちは自分のノートに三角定規を写し取ったり、三角定規に直接分度器を当てたりして角度を調べます。
そのとき、この子が話しかけてきました。
その子はずっとノートに図形と式を書いてそれを見つめています。
「これ、三角定規だけかな?ほかの三角形も180度なのかな?不思議だな?」
少し早めな口調で話します。
いつもは3分の1で終わるノートが下まで書かれています。
「面白いことに気付いたね。他の三角形はどうなのかな?」と聞くと、「他の三角形も180度のような気がするな。」と返してくれました。
みんなで角度を確認する時間になりました。
角度をどんどん発表することに満足していく子どもたち。
わかったわかった!三角定規はなんだかキリがいい角度だね。
最後にさっきの女の子が手をあげました。
「私ね、全部たしてみたの。すると180度になったんだよ。」
立って俯いてノートに話します。
みんなは「ん?今は角度を調べるんじゃないの?」と思っていたはずです。
そこに「俺もそう思ってたんだよね。」と男の子が式を出してくれました。
ようやく子どもたちが気付き「あぁ!すごい!」と喜びます。「直角以外をたすと必ず90度になって180度だ!」と三角定規のおもしろい仕組みを見いだしていったのです。
その子が授業中にどんどん話すことはその時までほとんどありませんでした。
でも、小さいかもしれない発見がその子を全体の場で話したいと思わせたのです。

レイチェル・カーソンの著作「センス・オブ・ワンダー」にこんな一節があります。
美しさの感覚、新しくて未知なるものに出会った時の興奮、共感や哀れみ、賞賛や愛情ーこうしたさまざまな感情がひとたび呼び覚まされたあとになってようやく、私たちは心動かされたその対象を、もっと知りたいと思うようになるのです。このようにして得られた知識はいつまでも、かけがえのない意味を持ち続けることになるでしょう。
「センス・オブ・ワンダー」は主に自然に対して抱く感情のことを指していますが、訳者の森田はこの「ワンダー」の訳について、以下のように述べています。
この言葉がもつ豊かな広がりを、日本語でどのように表現すればいいだろうか。どこに進むのでも、たどり着くのでもなく、ただ心がいきいきと躍動している状態。驚異、驚嘆、驚き、不思議、好奇心、あるいは文脈によっては、疑念や不安と訳されることもある。静かでありながら、繊細に周囲に感応している。「ワンダー」という言葉から、僕はこのような心の風景を思い浮かべる。
先ほどの子の姿と重なって見えてくるのです。自然との出会いではなくても、きっとこの子の心は「ワンダー」を感じていたのではないか。もちろん、その子に「いつまでも、かけがえのない意味を持ち続ける」までとはいかないと思います。それでも、その瞬間のきっとあった、小さな「ワンダー」は人の行動を変えるのです。
毎日の授業のどこかに「ワンダー」を。
そして、どの子の心にも小さな「ワンダー」を。
そういう体験が生まれる授業を思い描いています。
この記事が気に入ったらサポートをしてみませんか?
