
【三角比】基本事項まとめ
高校生になって数学を勉強していくと、
おそらく一番最初に直面する不思議な概念が
「三角比」
じゃないでしょうか?
中学生までに出てきていない
sin、cos、tan、$${\theta}$$
なんて記号が繰り広げられるこの分野。
嫌になる人も多いでしょう。
でも慣れてきたらそんなに難しいものではないんです。
ここでは、数Iの三角比で出てくる重要な公式と、
なぜそれが成り立つのかをまとめました。
基本のおさらい
まずは基本のおさらい。
sin、cos、tanの定義です。
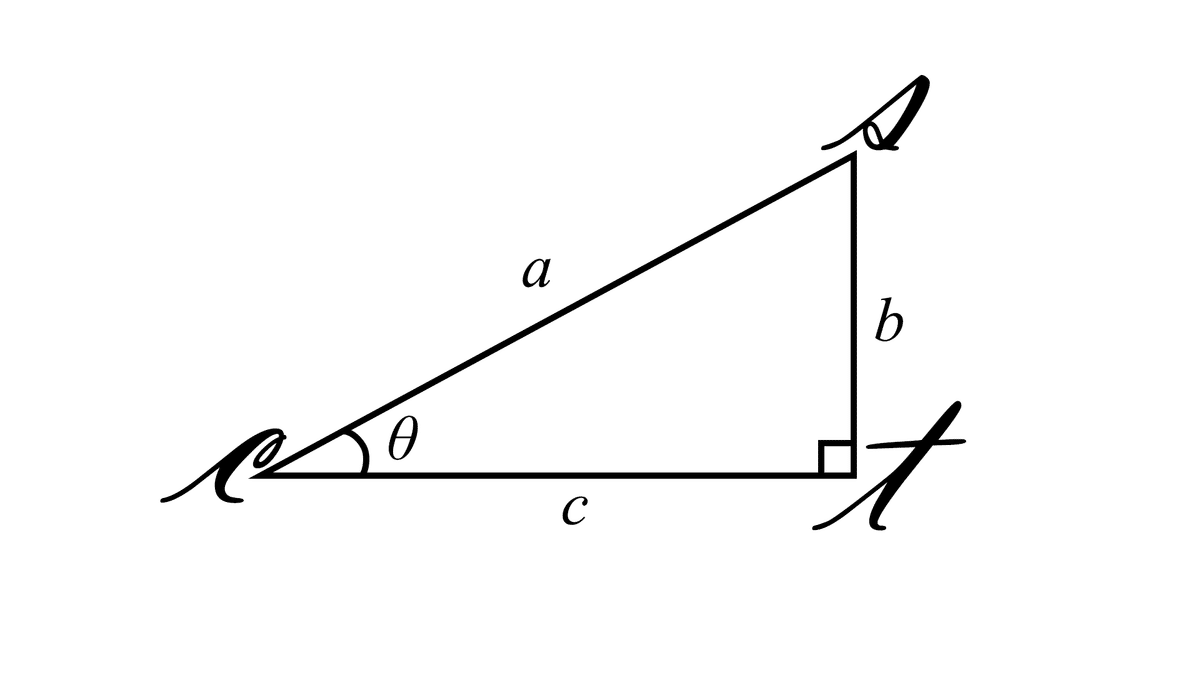
上の図のとき、
$$
\def\arraystretch{3}
\begin{align*}
\sin\theta &= \frac{b}{a} \\
\cos\theta &= \frac{c}{a} \\
\tan\theta &= \frac{b}{c} \\
\end{align*}
$$
でしたよね。
これは誰でも最初に教わると思います。
アレンジして便利に
上の基本の式を少し変形して、
$$
\def\arraystretch{3}
\begin{align*}
b &= a\sin\theta \\
c &= a\cos\theta \\
b &= c\tan\theta \\
\end{align*}
$$
と言う表現で覚えている人は意外と少ないのではないでしょうか?
教科書にもあまり書いていないと思います。
実は、この表現で覚えることが結構便利なんです。
特にsinとcosの式。
なぜかと言うと、
斜辺$${a}$$と角度$${\theta}$$が分かっているときに、
他の2辺をすぐに出せるから。
こんな感じで↓


特に物理をやっているときに役に立ちますので、
物理を学んでいる人には是非知っておいてほしい表現です。
超重要公式2選
高校1年生で最重要と言える公式が2個あります。
それが、
$$
\def\arraystretch{3}
\begin{align*}
\sin^2\theta+\cos^2\theta &= 1 \\
\tan\theta &= \frac{\sin\theta}{\cos\theta} \\
\end{align*}
$$
この2つです。
合わせて教科書では
$$
\tan^2\theta + 1 = \frac{1}{\cos^2\theta}
$$
も紹介されているかもしれません。
でも、これはそんなに重要ではないです。
なぜかと言うと、
一つ目の重要公式
$$
\sin^2\theta+\cos^2\theta = 1 \nonumber \\
$$
これの両辺を$${\cos^2\theta}$$で割ると、
$$
\def\arraystretch{3}
\begin{align}
\frac{\sin^2\theta}{\cos^2\theta}+\frac{\cos^2\theta}{\cos^2\theta} &= \frac{1}{\cos^2\theta} \nonumber \\
\tan^2\theta + 1 &= \frac{1}{\cos^2\theta} \nonumber
\end{align}
$$
となって、出てくるんです。
結局、最初の2つの式があればOKってことです。
なので、覚えなくても良いです。
実際、私は覚えていません。
ちなみに、この2式が成立する根拠はこちらの記事で解説しています。
まあ、この根拠は分からなくても良いです。
ただ、めちゃくちゃ重要な2大公式なので、絶対に覚えてくださいね。
「常識」になるまで、いろいろな問題で練習してほしいです。
正弦定理と余弦定理
正弦定理と余弦定理もかなり大事な定理ですね。

$$
\frac{a}{\sin A}= \frac{b}{\sin B}= \frac{c}{\sin C} = 2R
$$
$$
a^2 = b^2 + c^2 -2bc \cos A
$$
これは丸暗記で構わないと思います。
詳しい出し方はこちらに記載しましたので、良ければどうぞ!
三角形の面積
最後に紹介するのは、三角形の面積の求め方です。
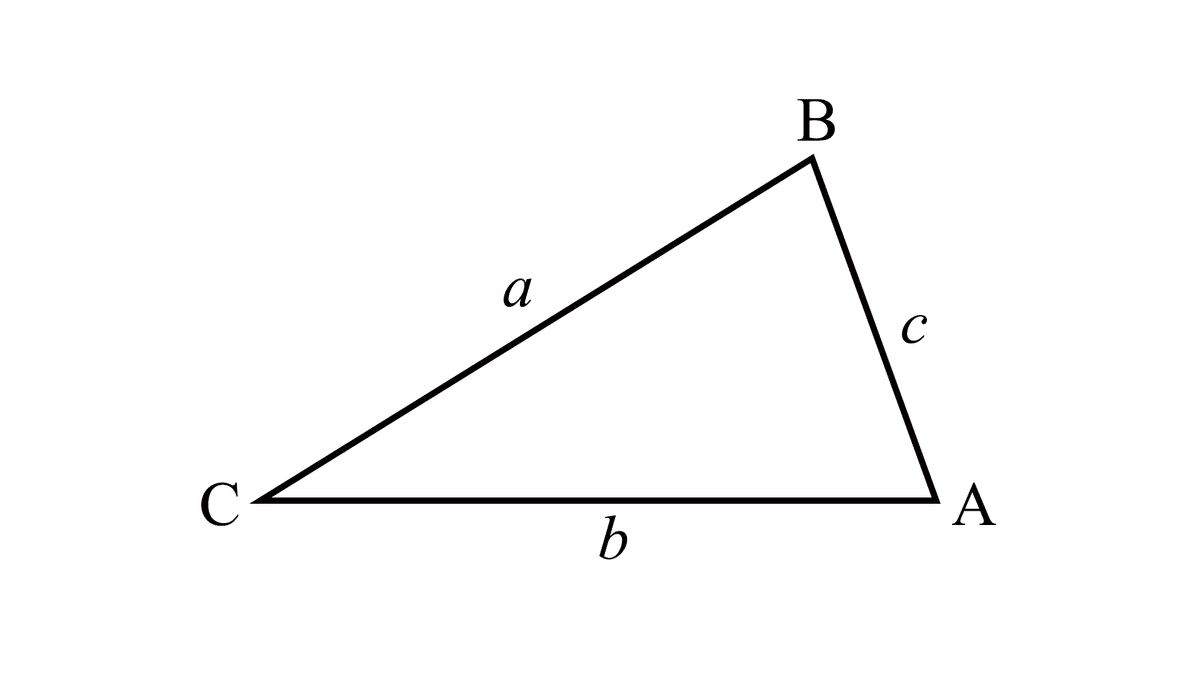
こんな三角形があったとして、面積$${S}$$は、
$$
S=\frac{1}{2}bc\sin{A}
$$
これも、実際上は公式的に暗記してしまって運用していくことが大半だと思いますが、成り立つ理由は下記に示しましたので、良かったら読んでみてくださいね。
覚える必要はないですが、ヘロンの公式についても記載していますので、是非どうぞ。
まとめ
以上です。出てきた式をまとめると
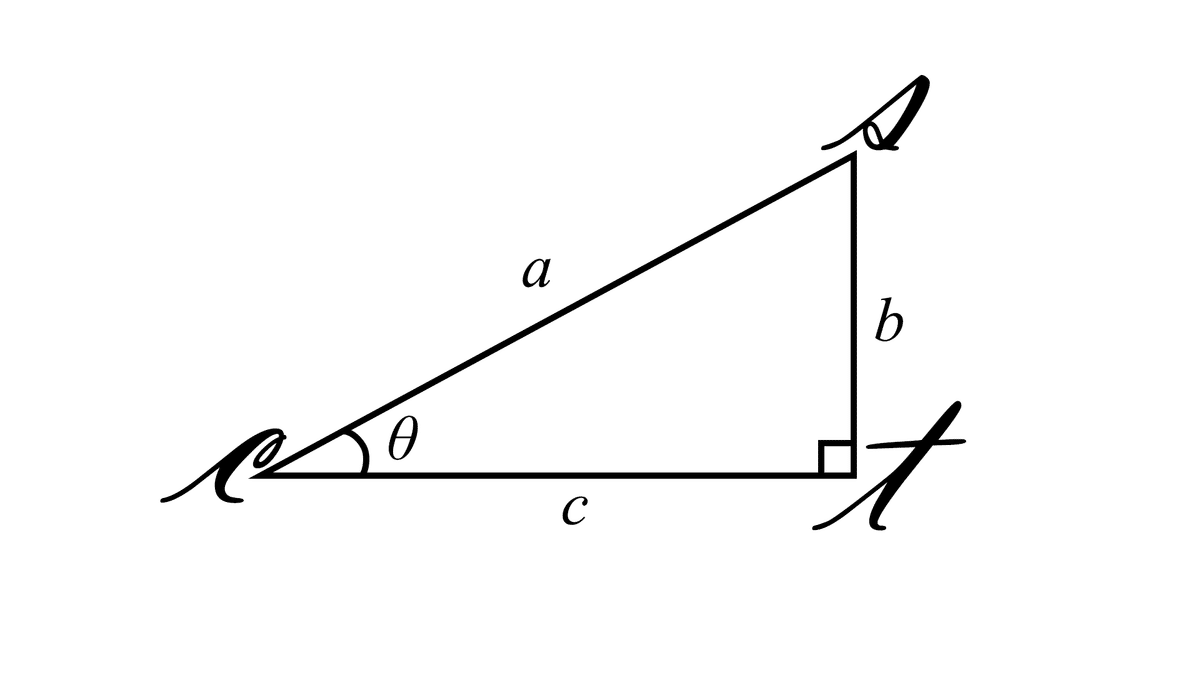
$$
\def\arraystretch{3}
\begin{align*}
\sin\theta &= \frac{b}{a} \\
\cos\theta &= \frac{c}{a} \\
\tan\theta &= \frac{b}{c} \\
\end{align*}
$$
$$
\def\arraystretch{3}
\begin{align*}
b &= a\sin\theta \\
c &= a\cos\theta \\
b &= c\tan\theta \\
\end{align*}
$$
$$
\def\arraystretch{3}
\begin{align*}
\sin^2\theta+\cos^2\theta &= 1 \\
\tan\theta &= \frac{\sin\theta}{\cos\theta} \\
\end{align*}
$$

$$
\frac{a}{\sin A}= \frac{b}{\sin B}= \frac{c}{\sin C} = 2R
$$
$$
a^2 = b^2 + c^2 -2bc \cos A
$$
$$
S=\frac{1}{2}bc\sin{A}
$$
以上です!どの式が何を意味しているのか、分かるようになるまで考えてみてくださいね。
最後に宣伝を。
もし、勉強に対する悩みや不安を感じているなら、ぜひ私たちのオンライン個別指導サービス【Your Guide】をご検討ください。
あなたの目標達成に向けて、丁寧にサポートいたします。
勉強の楽しさを再発見し、自分のペースで確実に成長していける環境を提供します。
興味のある方は、ぜひお気軽にお問い合わせください。
あなたの未来への一歩を、私たちが全力でサポートします。
