
高校物理のためのベクトル
高校物理では色々な数学を使います。
ベクトルの考え方もとても大事です。
高校のカリキュラム的には、数学Bから数学Cに移され、学ぶタイミングが遅くなってしまう高校も多いことでしょう。
物理で使いそうな話に的を絞って、簡単に紹介します。
※よく分からなくても、とりあえず流し読みしてください。何回か読めばきっと分かると思います。
ベクトルとスカラー
そもそもベクトルとは何なのか、と言うと「向きを持つ量」のことです。
例えば速度。速度には方向性がありますよね。
一方で、「向きを持たない量」のことを「スカラー」と言います。
例えば質量。どこかの向きに対して何グラム、と言った概念ではないですよね。
また、注意しなければならないことがあります。先ほどの「速度」に対して、「速さ」と言った場合、これは向きを持たない量として扱います。つまりスカラーなのです。端的に言えば、速度の大きさを速さと言うわけです。
速さ60km/hで走っている車、という言い方の場合、どの方向に走っているかは分かりませんが、言葉の使い方は問題ありません。
速度60km/hで走っている車、という言い方はよくないです。速度と言った以上、方向も明示すべきです。
ベクトルは記号の上に矢印を書いて表したりします。例えば速度は
$$
\vec{v}
$$
のように。
矢印が付いていないただの$${v}$$はスカラーとして扱います。
大学以降の表記法
ちなみに、大学以降では矢印を書くのを省略して、太字で表したりします。
つまり、
$$
\vec{v}=\bm{v}
$$
ということ。
とはいえ、手書きで太字は難しいです。この表記は活字の場合だと思ってください。手書きの場合は、太字にする代わりに記号のどこかに線を入れて、これはベクトルですよ、ということを明示します。書き方をまとめるとこんな感じです。

高校のうちは、矢印の表記しかしないので気を付けて下さい。
ベクトル・スカラー具体例
方向性のある物理量はすべてベクトルです。以下に例を挙げます。
$$
\def\arraystretch{1.5}
\begin{array}{ll}
物理量 & よく使われる記号 \\ \hline
位置 & \bm{x} \\ \hline
速度 & \bm{v} \\ \hline
加速度 & \bm{a} \\ \hline
力 & \bm{F} \\ \hline
運動量& \bm{p} \\ \hline
角速度 & \bm{\omega} \\ \hline
圧力 & \bm{P} \\ \hline
電場 & \bm{E} \\ \hline
磁束密度 & \bm{B} \\ \hline
\end{array}
$$
方向性のない、ただ大きさのみを表す物理量はスカラーです。以下に例を挙げます。
$$
\def\arraystretch{1.5}
\begin{array}{ll}
物理量 & よく使われる記号 \\ \hline
時間 & t \\ \hline
質量 & m \\ \hline
エネルギー & E \\ \hline
仕事 & W \\ \hline
熱 & Q \\ \hline
振動数 & f \\ \hline
波長 & \lambda \\ \hline
電荷 & q \\ \hline
電位 & V \\ \hline
\end{array}
$$
もちろんまだまだありますが、方向性の有り無しをイメージしてみてくださいね。
分解と合成
ベクトルには方向があるので、矢印で表現することが多いです。
矢印は他の方向に分解したり、2個以上の矢印を合成したりすることができます。イメージは以下の通り。

$$
{\bm{v}}={\bm{v}_x}+\bm{v}_y
$$
ということになります。つまり、
$${\bm{v}}$$を$${\bm{v}_x}$$と$${\bm{v}_y}$$に分解することもできるし、
$${\bm{v}_x}$$と$${\bm{v}_y}$$を合成して$${\bm{v}}$$にすることもできるということです。
平行四辺形を形成するように気を付ければどんな方向にも分解可能です。
この分解と合成はいろいろな場面で必要なテクニックです。
よくあるケース
例えば以下のようなケースはよく見かけます。

重力$${mg}$$を斜面方向と斜面に垂直な方向に分解しています。
こうすることで、地面ではなく斜面を水平面($${x}$$軸)として考えることができるわけです。考えやすくなるってことです。
以下はドップラー効果の問題で見かけるケースです。

自分に対して斜めに動いている物体の速度を、自分に向かってくる方向のみ抽出したいため、分解をしています。
他にもいろいろとあるのですが、キリが無いのでこのあたりにしておきます。
とにかく矢印(ベクトル)は分解できる!ということです。
自分に都合のいいように、遠慮なく分解してください。
成分表示
ベクトルを分解したら、それぞれの方向にどれだけの大きさなのか、と言う意味を込めた表し方をすることができます。多くの場合、$${xy}$$平面を考えて分解しますので、たとえば以下のような場合、

ベクトル$${\bm{p}}$$は、
$$
\bm{p} = (4,3)
$$
と言うように表します。これを成分表示と言います。
慣例的に、$${x}$$、$${y}$$の順で書きます。
ベクトルは2次元とは限りません。方向性があればベクトルなので、3次元でもOK。そうなると、最後に$${z}$$座標を入れます。
ベクトルの掛け算
ベクトル同士を掛け算するとどうなるでしょうか?
実は、ベクトルの掛け算には内積と外積という2つの概念があるのですが、高校数学では内積のみ取り扱い、外積は大学以降になります。
内積
ですので、まずは内積についてお話します。
内積というのは、方向を合わせて大きさを掛け算することです。
と言っても良く分からないので、具体的な事例を考えていきます。
例えば仕事を計算するときは、力×動いた距離、見たいに覚えている人も多いでしょう。でも、力を書けている方向と動いた方向がずれていたら、そのままかけてはいけないのです。しっかり方向を合わせてから、その成分をかけ合わせないとダメなのです。
つまり、以下のようなイメージです。
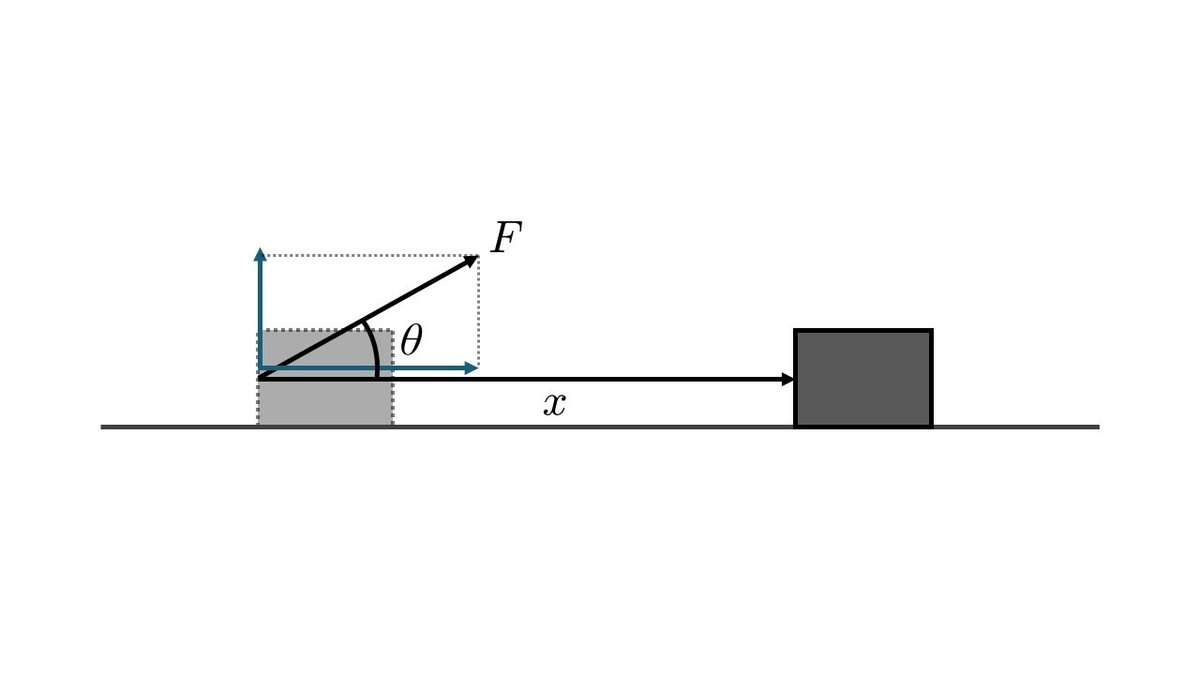
物体を、力$${F}$$で斜め上に押したら、距離$${x}$$動いた場合。この場合は仕事は$${W=Fx}$$とはなりません。$${F}$$を$${x}$$の方向にあわせて上げないといけないのです。
結果、$${F \cos{\theta}}$$となるので、$${W=Fx\cos{\theta}}$$となります。
ここでは力を分解して、その成分の積を書いたのですが、2つのベクトルの内積は下記のようにも表せます。
$$
\bm{F} \cdot \bm {x}
$$
$${\cdot}$$(ドット)を使うのです。数学でも、掛け算するときに$${\times}$$の代わりに使うことも多いですよね。
結局
$$
W=\bm{F} \cdot \bm {x}=Fx\cos{\theta}
$$
となります。この$${\cos{\theta}}$$が出てくる式が教科書にはいくつか書いてあるはずですが、だいたい内積の考え方をしていると思えば良いでしょう。
そしてもう1つ触れておきたいことは、ベクトルの内積はスカラーになるということ。今回も、力と変位という、方向性のある2つの量でしたが、内積を取ると仕事という、方向性のない量になりました。内積はそいういうものなので、不安にならなくて大丈夫です。
ちなみに、内積の場合は$${\times}$$は使ったらだめなんです。
実は、この$${\times}$$を使うと、内積ではなく外積を計算をするという意味になるのです。ちなみに内積と違って、外積はベクトルになります。
外積
外積は、高校ではやりませんので、大学受験には不要な知識です。
といっても、実は高校物理の内容でも外積の概念が適用できる場面があります。
ですので、物理が好きな人は知っておいて損はありません。
外積が関係する高校物理の内容には以下のようなものがあります。
力のモーメント($${\bm{M} = \bm{d}\times\bm{F}}$$)
ローレンツ力($${\bm{F} = q(\bm{v}\times\bm{B})}$$)
では、外積の計算方法を簡単に説明します。
外積は、2つのベクトルのつくる面積を大きさに持つ、両方のベクトルに垂直な成分のベクトルになります。以下のようなイメージです。

この図で、$${\bm{a}}$$と$${\bm{b}}$$が作る平行四辺形の面積の大きさが、$${\bm{c}}$$の大きさに合致するということ。
そして、$${\bm{c}}$$の方向は$${\bm{a}}$$と$${\bm{b}}$$に垂直な方向になります。必然的に3次元になりますね。
ここで、あれ?と思った人もいるでしょう。垂直な方向と言っても2通りあるので、どちらになるの?と言う感じですよね。
これは、実はかける順番によって決まります。
上の図の場合は、
$$
\bm{a} \times \bm{b} = \bm{c}
$$
という順番の外積になっていて、このとき、$${\bm{a}}$$から$${\bm{b}}$$側に右ねじを回したときにねじが進む方向が$${\bm{c}}$$の方向になります。

つまり、外積は、かける順番が大事ということになります!
逆にすると、計算結果(の符号)が逆になるのです。
ローレンツ力の公式は高校でも出てきますが、その際は力の方向はフレミングの左手の法則で出すことになっていると思います。
あれは外積の計算でも同じ結果が得られます。
ですので、公式を覚える際は順番も意識しておくとよいでしょう。
計算法まで細かくやると行き過ぎた内容になりそうなので、このあたりで終わりにしたいと思います。
まとめ
以上、本当にざっくりと、ベクトルについてまとめてみました。
矢印は他の方向に分解できる!
このことを特に意識してもらえれば、他のことは些細なことですので、深く考えなくても不都合はないかもしれません。
学習の役に立てば幸いです。
最後に宣伝を。
もし、勉強に対する悩みや不安を感じているなら、ぜひ私たちのオンライン個別指導サービス【Your Guide】をご検討ください。
あなたの目標達成に向けて、丁寧にサポートいたします。
勉強の楽しさを再発見し、自分のペースで確実に成長していける環境を提供します。
興味のある方は、ぜひお気軽にお問い合わせください。
あなたの未来への一歩を、私たちが全力でサポートします。
