
Enhancing Variational Quantum Circuit Training: An Improved Neural Network Approach for Barren Plateau Mitigation
Blood Huntについて
MARVELコミックをよく買うのですが、今年の春頃から連載されていた"Blood Hunt"シリーズが先日まとまって売られていたのでつい買っちゃいました。

まだ読んでないので詳しくは分かりませんが、どうやらブレイドが反乱を起こしてNYをヴァンパイアで埋め尽くそうとしているらしいです。
そして我が推しドクター・ドゥームの活躍()もあるようなので非常に楽しみですね。
ただ、未読のコミックがまだ20冊以上あるのでこのバックログをどうにか片付けたい…。
概要
Enhancing Variational Quantum Circuit Training: An Improved Neural Network Approach for Barren Plateau Mitigation
written by Zhehao Yi, Yanying Liang, Haozhen Situ
published on Thu, 14 Nov 2024
[Abstract]
Combining classical optimization with parameterized quantum circuit evaluation, variational quantum algorithms (VQAs) are among the most promising algorithms in near-term quantum computing. Similar to neural networks (NNs), VQAs iteratively update circuit parameters to optimize a cost function. However, the training of variational quantum circuits (VQCs) is susceptible to a phenomenon known as barren plateaus (BPs). Various methods have been proposed to mitigate this issue, such as using neural networks to generate VQC parameters. In this paper, we improve the NN-based BP mitigation approach by refining the neural network architecture and extend its applicability to a more generalized scenario that includes random quantum inputs and VQC structures. We evaluate the effectiveness of this approach by comparing the convergence speed before and after it is utilized. Furthermore, we give an explanation for the effectiveness of this method by utilizing a loss landscape visualization technique and the expressibility metric of VQC. The smoothness of the loss landscape offers an intuitive insight into the method's utility, while the reduction in expressibility accounts for the enhanced trainability. Our research highlights the universal applicability of the NN-based BP mitigation approach, underscoring its potential to drive progress in the development of VQAs across diverse domains.
[Abstract(翻訳)]
古典的最適化とPQCの評価を組み合わせた変分量子アルゴリズム(VQA)は、近い将来の量子コンピューティングにおいて最も有望なアルゴリズムの1つである。ニューラルネットワーク(NN)に類似して、VQAは回路のパラメータを反復的に更新し、コスト関数を最適化する。しかし、変分量子回路(VQC)の学習は、"Barren Plateau (BP)"として知られる現象に影響されやすい。この問題を軽減するために、NNを使用してVQCのパラメータを生成する方法を含む、さまざまな手法が提案されてきた。本研究では、NNベースのBP軽減手法をNNのアーキテクチャを洗練させることで改善し、ランダムな量子入力やVQC構造を含むより一般化されたシナリオにもその適用性を拡張する。本手法の有効性を、利用前後の収束速度を比較することで評価する。さらに、損失ランドスケープの可視化技術とVQCの表現力の指標を用いて、この手法の有効性について説明を行う。損失ランドスケープの滑らかさは手法の有用性について直感的な洞察を与え、表現能力の減少は学習性能の向上を説明する。我々の研究は、NNベースのBP軽減手法の普遍的な適用可能性を強調し、多様な分野でのVQA開発の進展を促進する可能性を示している。
コンテンツ
VQAとBP問題、そしてNNを使った軽減の可能性
量子コンピュータは長年の研究と開発により、驚くべき進歩を遂げてきた。
中でも変分量子アルゴリズム(VQA)は、NISQ時代に適応するように設計された量子-古典ハイブリッドアルゴリズムで、多様な複雑な問題を解決することを期待されている。
VQAは、量子状態としてエンコードされたデータを処理し、その測定結果をコスト関数の計算などに使用する量子コンポーネントと、測定結果に基づいて変分量子回路(VQC)内のパラメータを調整する古典コンポーネントによって構成されている。
代表的なVQAには、組合せ最適化問題の近似解を効率的に求めるQAOAや、量子系の基底状態エネルギーを近似的に求めるVQE、量子および古典データを生成するQGANなどがある。
VQAの進展にも関わらず、依然として克服すべき課題がある。
"Barren Plateau (BP)"はコスト関数の選択や量子状態のもつれ、ノイズの存在などを原因として発生する勾配の無い状態を指す。
量子ビット数の増加により、考えられる量子状態の規模が大きくなり、損失関数の勾配が非常に小さくなるためグローバル最適解への収束が極めて困難になる。
これまでにBPの問題を緩和するために多くの手法が提案されてきたが、中でも注目されるのはニューラルネットワーク(NN)を用いたアプローチである。
この方法ではより高速な収束を実現し、BP問題を軽減する可能性を示す一方で、エンコードするデータが古典データに限定されることやVQC構造が固定されたものとして設計されることなどの制約があった。
本研究では、NNベースのBP軽減アプローチを改良し、VQCの入力をランダムな量子状態に拡張し、構造をランダム一般化し、NNアーキテクチャを最適化する。
表現能力
表現能力(Expressibility)は、ヒルベルト空間内の様々な量子状態を生成する能力を定量化する指標である。
VQC $${\mathcal{U}(\theta)}$$ の表現能力 $${Expr}$$ は、KLダイバージェンスを用いて次のように与えられる。
$${Expr = D_{KL}(P_{\mathcal{U}}(F) || P_{Haar}(F)) = \sum_F P_{\mathcal{U}}(F) \ln \frac{P_{\mathcal{U}}(F)}{P_{Haar}(F)}}$$
表現能力の推定には次の3ステップを用いる。
入力状態として $${|0\rangle}$$ を設定し、量子回路のパラメータをランダムに選択し、 $${2K}$$ 個の量子状態を生成、これを $${K}$$ 組のペアに分ける。
各ペアのFidelity $${F = |\langle \phi_1 | \phi_2 \rangle|^2}$$ を計算し、 $${K}$$ この値を取得する。
Fidelityの値のヒストグラムから $${P_{\mathcal{U}}(F)}$$ を求め、 $${P_{Haar}(F)}$$ と比較してKLダイバージェンスを計算する。
この表現能力の値が小さいほど量子回路は望ましい解に到達しやすい一方で、BPの影響を強く受けてしまう。
Barren Plateau
BPの原因としては、コスト関数にグローバルな観測量を用いていることやランダムなエンタングルメントを生成していること、局所的なPauliノイズなどが挙げられる。
対策としては、層ごとに段階的に学習を行う方法や、メタラーニングを使用して他のタスクから得た知識を初期パラメータに適用する方法などがあった。
また、NNを用いたアプローチではBP問題を大幅に改善することが見込まれている。
数値実験において、NNが生成したパラメータをVQCの変分箇所に適用すると、BP問題の影響が軽減され、収束速度が向上した。
方法
VQCの変分箇所に注目するため、ランダムな量子状態を入力とすることで一般化を図る。
また、VQCの構造もランダムなものに拡張する。
具体的には、各量子ビットに $${U = R_z(\theta_1)R_y(\theta_2)R_z(\theta_3)}$$ を適用し、ランダムに選んだ量子ビットペアに $${CZ}$$ ゲートを適用、その後1量子ビットの回転ゲート $${R_y, R_z}$$ を追加したものを考える。

パラメータ数としては、量子ビット数 $${N}$$ とゲートブロック数 $${L}$$ を使って $${3N + 4L}$$ となる。
標準量子回路(SQC)とニューラル強化量子回路(NEQC)のモデルでの学習過程は以下のとおりである。
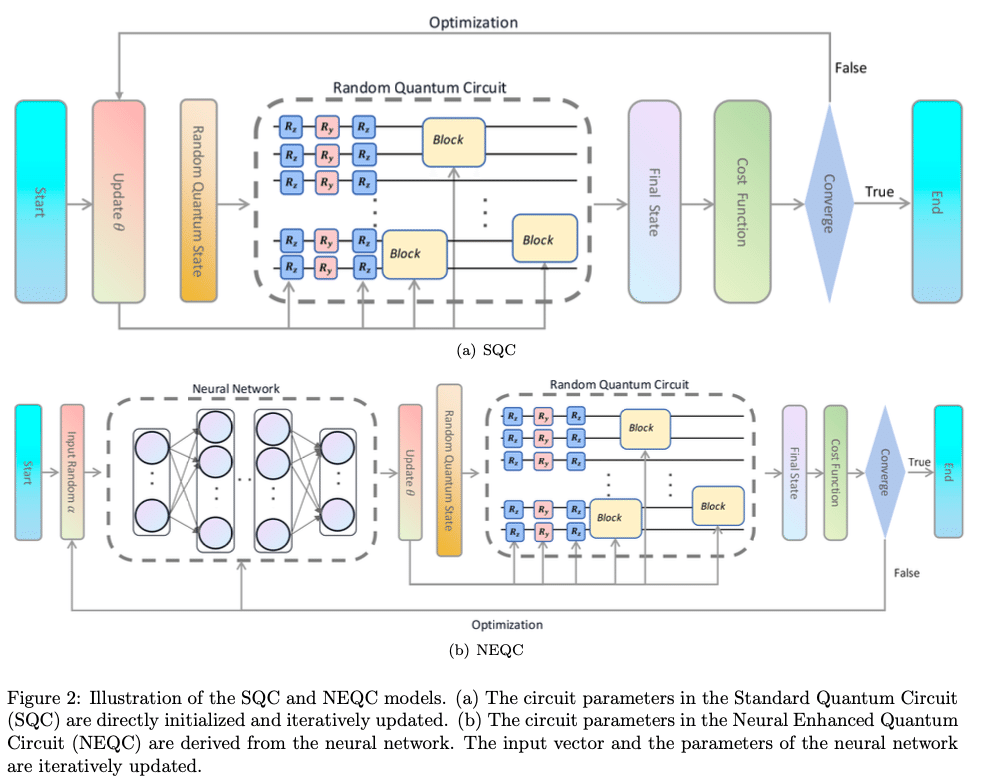
先行研究におけるNEQC(NEQC-NN)と本研究で扱うNEQC(NEQC-CNN)のアーキテクチャの違いを以下に示す。

本研究で用いるコスト関数は次のものである。
$${C = 1 - \frac{1}{N} \sum_i Tr[(| 0 \rangle \langle 0 |_i \otimes I_{\bar{i}}) \rho]}$$
ここで、 $${| 0 \rangle \langle 0 |_i}$$ は第 $${i}$$ 量子ビットに作用する演算子、 $${I_{\bar{i}}}$$ はその他の量子ビットに作用する恒等演算子、 $${\rho}$$ は量子回路の出力状態である。
全ての量子ビットの測定結果が0であることは $${C = 0}$$ であることと等価であり、任意の量子状態 $${| \Phi \rangle}$$ を $${| 0 \rangle^{\otimes N}}$$ に変換するように量子回路を学習することでコスト関数の最小化を図る。
SQC、NEQC-NN、NEQC-CNNの3つのモデルを、収束までにかかる反復回数、パラメータ空間におけるコスト関数の滑らかさを3次元プロットで可視化したランドスケープ、表現能力の3つで評価し比較する。
数値実験結果
数値実験の設定として、量子ビット数 $${N}$$ を3〜8にし、ブロック数 $${L}$$ を $${L = \lceil N^2 \ln N \rceil }$$ とする。
各量子ビット数の実験に対し、SQC、NEQC-NN、NEQC-CNNの3つのモデルを独立に10回ずつ学習を実行する。
最適化器にはモーメント付きSGDを用い、ロスの値が0.001を下回るか、100イタレーションごとにロスの算出を行い、ロスの変化値が0.0001を下回ったら学習を止める。
環境としては、PyTorchとTensorCircuitフレームワークを使用してモデルを構築および学習を行う。
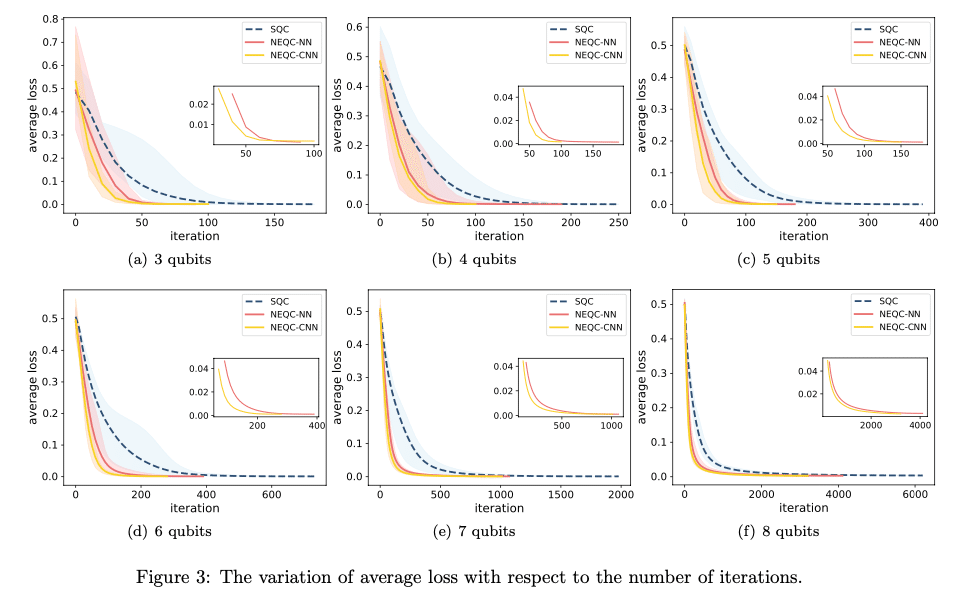
図を見ると、NEQCモデルはSQCモデルよりもはるかに少ない反復回数で収束することがわかる。
量子ビット数が増えるにつれ、収束に必要な反復回数は全てのモデルで増加しているが、NEQCモデルはSQCモデルに比べて緩やかに増加しており、高いスケーラビリティを示している。
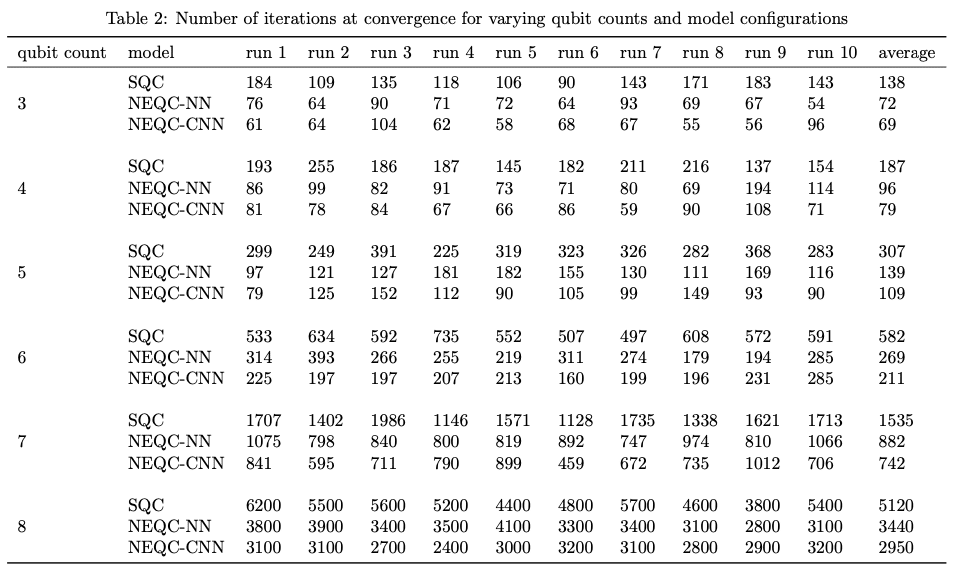

コスト関数のランドスケープを3次元プロットで可視化して、モデルの比較分析をした。

この図は左から順に、SQC、NEQC-NN、NEQC-CNNのモデルを表し、縦方向には上から順に3量子ビット〜8量子ビットのランドスケープを表す。
結果としては、NEQCモデルはSQCモデルよりも滑らかであり、滑らかなランドスケープは勾配が大きくなる傾向があるため、結果的にBPの影響を軽減できる。
最後に、それぞれのモデルの表現能力を比較する。

これから、NEQCモデルがSQCモデルより圧倒的に高い表現能力の値になっていることがわかる。
前述した通り、表現能力の値が低いとBPの影響を受けやすいので、明らかにNNで生成したパラメータを持ったVQCの方がBPに強いことが示せた。
結論
本研究では、ランダムな量子状態のエンコーディングから、ランダムなVQC構造の学習におけるBP問題の軽減を行なった。
NNベースのBP問題へのアプローチは、標準的なVQCに比べ非常に優れたものとなった。
QAOAやVQEなどの量子アルゴリズムにも適用できるため、汎用性の高いモデルとして多くの分野で活躍が見込める。
感想
なんか、わかるようでわかんないですね。
CNNモデルに置き換えて、確かに少し良くなったのかもしれないですが、結論としてSQCとNEQCを比較してNEQCが優れているという持っていき方なので、そこのところ先行研究で十分だったんじゃ…?と思ってしまいますね。
まあ、ニューラルネットワークで忌まわしきBarren Plateauが軽減出来るのならそれに越したことないんですが、今回もたった8量子ビットまでしか扱っていないのに収束までに何千回と回さなきゃいけないなんてそんな馬鹿げた話ねぇ。
IBMの実機に突っ込んだら一瞬で1ヶ月の上限超えちゃいますよね。
