一般と特殊、あるいは抽象と具象

デカルトは『方法序説』第二部において、問題解決の方法を述べている。
まずは「疑う」ということを、理性によって喚起し、自分が納得しないものを「鵜呑み」にしないことが、これから生きていくうえで大切なことだと説いている。

彼が論理学、ことに幾何学において論理的取り組み方を四つの方法で示している。
①私が明証的に真であると認めるのでなければ、どんなことも真として受け入れない。疑いをさしはさむ余地のまったくないほど明晰かつ判明に精神に現れるもの以外は、何も私の判断の中には含めない。
②私が検討する問題の一つ一つをできるだけ多くの、しかも問題をよりよく解くために必要なだけの小部分に分割すること。
③私の思考の順序にしたがって、単純なものからより複雑なものへ認識の段階を踏んで解決に向かうこと。
④最後に、見直して見落としのないことを確かめること。

デカルトは若いころ、カトリック系の学校に通わされていた。
そこで、数学や論理学に出会い、また社会学的な分野や占星術や錬金術に至るまでの、その道の学者によって恣意的な論理で構築されているような学問にも触れ、その矛盾や不可解な論理に不満と疑問を抱くにつれ、自分が理性的に真であると思えるもの以外は捨て去ることにしたと述べている。
とくに「耳学問」や、書物中心の学習では陥りやすい「鵜呑み」に気をつけなければならないと早くから気付いていたらしい。
これには私もいささか耳が痛いと思った。
「情報リテラシー」にもかかわる、重要な学ぶための心構えだと思う。

ここで、デカルトも思索の上で使ったであろう思考の概念を図式化してみる。

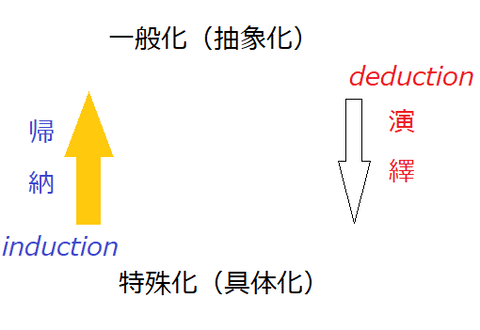
論理には、「一般化」と「特殊化」の間に行き来がある。
アインシュタインの「一般相対性理論」と「特殊相対性理論」が典型だろう。
ここで一般化と抽象化は同じ意味と考えてもらっていいし、特殊化と具体化（もしくは具象化）も同じ意味と考えてもらっていい。
相対性理論でもそうなのだが、まず特殊な例から帰納法によって一般化されるような論理立てが、数学などの論理学の学問では多い。
数学的帰納法は数列の一般項を求める場合などで使われる。
ところが社会学などで、事例がちまたに溢れている場合に、そこから何かしらの法則性を見出し、特殊解を求める（演繹する）、とういうような微分方程式を立てて一般解と特殊解のようなものを求める作業もある。

数学と算数の違いは、おそらく算数が「特殊化」の学問であり、数学が「一般化（抽象化）」の学問だというようなことだろうか？

このように演繹法と帰納法を使って、デカルトも理性に従って論理立てていったものと考えられる。

そしてデカルトのいいところは、常に内省的であり、④にあるような「見直し」をちゃんとおこなっているところだろう。

PDCAサイクルを彼は、すでに使っていたのだと思うと、頭が下がる思いだ。
※Plan,Do,Check,Actの頭文字で「計画、実施、検証、改善」を作業現場で回す、QC活動の一環

無人島に持っていく本に『方法序説』は絶対だ。