
第20話 回るあまりと循環するシャッフル
「とりあえず、ここまでをおさらいしとこか。」
高木がホワイトボードをいったんぜんぶ消して、これまでの内容をまとめた。
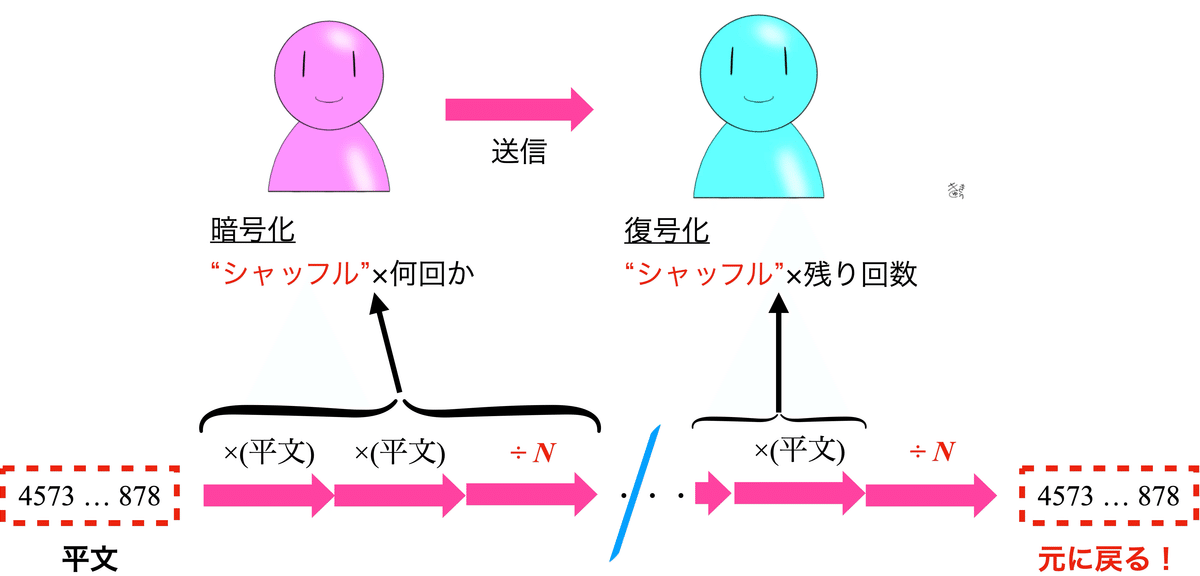
「RSA暗号の背後にあるのは、数字が循環するっていう法則。“ある操作” ––– “シャッフル”って呼ぶとして ––– 平文を一定回数だけシャッフルしてやると、元の平文に戻るわけやな。」

「で、そのシャッフルには、平文と公開鍵$${N}$$を使うと。」

「あるいは、さっき君が証明してくれたとおり、『平文のかけ算だけ先に済ませて、あまりを求める計算は最後に$${1}$$回だけやる』でもええ。」

「平文を暗号化するときは、平文に戻る前の中途半端なところでシャッフルを止めるわけやな。」
大翔が説明を引き取った。
「そうそう。受信した人は、残り回数分だけシャッフルしたらええ。ただし、今言った方法で計算するなら、暗号化の最後にあまりを求める計算が入るけどね。」(※1)
「で、その暗号化するときの回数っちゅうんが、もう1つの公開鍵$${e}$$のことなんやな?」
「そう。$${e-1}$$回やね。」(*1)

「で、あと残ってるんは復号化のやり方やな。」
ここまでの説明を聞く限り、シャッフルには毎回平文そのものが必要になる。復号化の計算も例外ではない。
「そやね。そこでやな。最初に『シャッフルを一定回数くり返したら平文に戻る』って話したやん? それを数式で書いてみてくれへん? シャッフルの別の計算法の方使って。」
「最初のヤツを? 別のヤツで?」

「いや、ちょっと待て。何回シャッフルしたらええか、俺知らんぞ?」
「それは僕かて知らんよ。ここは、数学のお決まりで行こうな。」
「・・・・・・。『〇〇を××とおく』いうヤツか。」
ついさっき、大翔自身も使ったやり方である。普段なら聞いただけでうんざりするフレーズだが、今の彼にはバフがかかっている。
「よっしゃええやろ。ええっと、なんておいたろうかな・・・?」
「提案。“$${f}$$”とかどう?」
「$${f}$$? 別にええけど、どっから出てきてん、それ?」
「それはまぁ、後で説明する。」
「? まぁほな、なんかようわからんけどそれで行こか。」
ふたたび平文を$${x}$$とおき、さきほどの図と照らし合わせてみる。

「つまり、こんな感じか?」
$${x^{f+1}}$$を$${N}$$でわったあまりは$${x}$$
「そうそう!」
「・・・・・・。」
大翔はアゴに手を当て、自分が書いた数字をしげしげとながめ、首を傾げた。
「どしたん?」
どこかしら既視感のある内容だが、いつ見た何なのか、まったく見当がつかない。見た場所は、ほぼ確実に近所の神社だが。
「いや・・・。なんでもない・・・。ほんで?」
「うん。その右肩の$${(f+1)}$$ってさ。現時点で値は不明、それどころか素数かどうかもわからへん。でも仮に、ある$${\textbf{2}}$$つの整数$${\textbf{e, d}}$$のかけ算で書けるとしたら、どうよ?」
「なんや。また新しい文字が出てきて・・・。いや、ちょっと待て?」
よく見ると、$${2}$$つのうちの片方は$${e}$$である。意味深だ。
「仮にお前の言うとおりやとすると・・・。」
ホワイトボードに書いた数式を、すこし書き直す。
$${x^{f+1}=x^{ed}=\left(x^e\right)^d}$$を$${N}$$でわったあまりは$${x}$$
「いいね。で、さっきも言ったとおり、暗号化の計算は、$${x}$$を$${e}$$乗して$${N}$$でわっても求められる。」

「つまり・・・、どうなる?」
高木に問われ、大翔はあらためて自分が書いた数式を見た。式には、今高木が口にした$${x^e}$$が入っている。
「つまり、こういうことか?」
$${x^{f+1}=x^{ed}=\left(x^e\right)^d=\left(\text{暗号文}\right)^d}$$を$${N}$$でわったあまりは$${x}$$
「イエス! これで謎解けたやろ?」(※1)
「はあー! なるほどな! 平文やのうて、暗号文自体を使たらええのか!」
「そう。シャッフルのやり方自体は暗号化のときと一緒やけど、平文の代わりに暗号文自体を使えばええわけやね。」

言われてみれば、先日吉栄光比売が、『RSA暗号を解くには、暗号文を複数回かけ算して$${N}$$でわったあまりを求めればいい』というようなことを言っていたような気がする。あれはこういう意味だったのか。
「そうと決まれば、さっそく!」
大翔は叔父からの宿題を開いた。
公開鍵:$${N=2077, e=283}$$
暗号文:$${1189, 465, 1500, 190, 907}$$
「たとえば、この$${1189}$$を$${d}$$乗して$${2077}$$でわったらええんやろ!? ・・・・・・。$${d}$$って何?」
「$${f+1}$$を$${e(=283)}$$でわった数。」
「$${f}$$って何?」
「さあ。」
「わからへんのかい!」
「まぁまぁ、そう慌てるなって。手がかりはあるやろ。」
そう言って、高木はお茶を一口飲んだ。
「手がかり?」
「そもそも、その$${f}$$ってどこで出てきたんやったっけ?」
「おん? それは・・・えっと?」
大翔は考えながら、自分がそれまで書いてきた数式をさかのぼって行った。
「ああ、これやん。」
$${x^{f+1}}$$を$${N}$$でわったあまりは$${x}$$
「やろ? ようするに、それが$${f}$$に対する条件式や。『$${x}$$を$${(f+1)}$$乗して$${N}$$でわったら$${x}$$に戻るような数』ってこと。」
「ええ?? そんな数あるかぁ?」
大翔は首を傾げた。
気をつけなければならないのは、文面に登場する未知数$${x}$$は、今回は主役ではないということだ。普段の授業なら、$${x}$$は何かしらの方程式の解であることがほとんどだ。それが登場すれば、生徒は(イヤイヤ)$${x}$$の値を求めようとする。
だが今回の問題では、求めなければいけないのは$${x}$$ではなく$${f}$$の方なのである。$${x}$$はどちらかというと助演である。
「いや・・・。むしろ$${x}$$ってなんでもええんちゃうんか? 平文なんやから。」
もし$${x}$$が特定の値でしかあり得ないのだとしたら、暗号化できない平文が存在することになる。暗号としては片手落ちだろう。どんな値でもいいのだとすれば、助演どころか、もはやエキストラだ。
「んん〜。“なんでも”は言い過ぎかな。一応、$${N}$$より小さい数っていう制約はあるよ。でもまぁ、それだけやね。」
「いや、ムリムリムリ! そんな都合のええ数があるとは思えん。」
「それがあるんよなぁ。実は、フェルマーの小定理って定理があってさ。」
「いや、めっちゃ知ってるぅ〜。」
「へ?! 知ってんの?」
高木が素っ頓狂な声を上げた。
ムリもない。数学弱者で通っていたクラスメイトがそんな定理を知っていたら、「3日会わない間に何があったのか」といぶかる方が自然だ。
「これやろ?」
大翔はカバンからメモ書きを取り出し、高木に見せた。
$${p}$$ は素数
$${a}$$ は $${p}$$ でわり切れない整数
このとき、$${a}$$ の $${(p-1)}$$ 乗を $${p}$$ でわったあまりは $${1}$$
「そうそう! なんや、知ってるんなら話は早い。この定理のおかげで、さっき言うてた$${f}$$が求められるねん。」
大翔はアゴに手を当て、メモ書きをじっくりとながめた。
たしかに先日、この定理から派生して、「あまりは回る」という話につながった。たとえば、$${10}$$は$${6}$$乗するごとに$${7}$$でわったあまりが$${1}$$になる。そして、それ以外のときはあまりがくり返しになるのである。

これは、「平文を一定回数シャッフルすれば元に戻る」という話にも通じる。さきほど、「$${x^{f+1}}$$を$${N}$$でわったあまりは$${x}$$」という文言を見たときに感じた既視感の正体はこれだったのだ。
だがこのフェルマーの小定理に関しては、大翔には苦い記憶もある。最初に叔父に教えてもらったとき、定理の前提を確認し忘れてしかられるという憂き目にあったのだ。
おかげで定理の前提をきっちりチェックするようにはなったのだが、だからこそ、今この流れでフェルマーの小定理が出てきたのには違和感がある。
「フェルマーの小定理やとさ。$${p}$$は素数で、$${a}$$は$${p}$$でわり切れへん数やん。とてもじゃないけど、今の話には役に立ちそうにないで?」
おそらく、$${p\rightarrow N, a\rightarrow x}$$とでも置き換えればいい、という話だろう。だが、$${N}$$は素数ではないし(昨日、素因数分解したばかりだ)、$${x}$$にいたっては$${N}$$未満の数すべてである。定理の前提条件をまるで満たしていない。
「ふっ。気づいたか・・・。さすがは・・・」
「相棒ではないから、とりあえず説明せぇ。」
「・・・・・・。たしかに、フェルマーの小定理だけでは荷が重い。実は、これをより一般化したオイラーの定理ってのがあってやな・・・。」
To Be Continued…
*1: 第19話の記載に誤りがありました。ここでは、訂正した内容に基づいた記載をしております。
進んだ注
以下、やや専門的な注釈になります。内容がわからなくてもストーリーには直接関係ないので、興味ある方だけご覧ください。
※1:厳密には、この指摘をするには以下の命題を証明する必要がある。
命題
$${x,n,m,N}$$を正の整数とする。また、$${x^m}$$を$${N}$$でわったあまりを$${y}$$とおく。この時、$${x^{mn}}$$を$${N}$$でわったあまりと$${y^{n}}$$を$${N}$$でわったあまりは等しい。
証明
題意より、適切な非負の整数$${\xi}$$に対し、
$$
\begin{equation}
x^m=\xi N+y
\end{equation}
$$
と書ける。
・$${n=1}$$の場合
$${x^{mn}=x^m=\xi N+y}$$であり、$${x^{mn}}$$を$${N}$$でわったあまりは$${y=y^n}$$に他ならない。よって成立。
・$${n=k}$$の場合
$${x^{mk}}$$を$${N}$$でわったあまりと$${y^{k}}$$を$${N}$$でわったあまりは等しいと仮定する。このとき、ある適切な非負整数$${\xi'}$$を使って
$$
\begin{equation}
x^{mk}=\xi' N+y^k
\end{equation}
$$
と書ける。
・$${n=k+1}$$の場合
式(1)より、
$$
\begin{equation*}
\begin{split}
x^{m(k+1)}&=\left(\xi N+y\right)^{k+1} \\
&=\left(\xi N+y\right)^{k}\cdot\left(\xi N+y\right) \\
&=x^{mk}\cdot\left(\xi N+y\right)
\end{split}
\end{equation*}
$$
式(2)より、
$$
\begin{equation*}
\begin{split}
x^{m(k+1)}&=\left(\xi' N+y^k\right)\cdot\left(\xi N+y\right) \\
&=\left[\left(\xi' N+y^k\right)\xi+y\xi'\right]N+y^{k+1}
\end{split}
\end{equation*}
$$
ここで、右辺第$${1}$$項は$${N}$$の倍数なので、あまりには寄与しない。よって$${x^{m(k+1)}}$$を$${N}$$でわったあまりは、右辺第$${2}$$項$${y^{k+1}}$$を$${N}$$でわったあまりということになるが、これが証明したいことであった。
よって数学的帰納法により、すべての正の整数$${n}$$に対し、題意が示された。
Q.E.D.
