
ペントミノ講座③ 組み換え可能な図形とは?
みなさんどうも、うつろです。
今回は線対称からは少し離れて、新しい概念のお話に移ろうと思います。
「組み換え可能な図形」
サムネイル画像を見てある程度は理解できるかもしれません。
勝手に見つけて適当に名前をつけたのでしっくりこなかったらすみません。
それでは本編。
線対称じゃないのに…
今回紹介する「組み換え可能な図形」は、ピースの位置を変えて2通りの方法で置ける図形のことを指します。線対称な図形との一番の違いは、当たり前ですが「線対称ではない」こと。
線対称な図形については下記の記事をご確認ください。
線対称な図形は対称軸を中心とすれば2通りの方法で置けるのはある意味当たり前。そういった意味で、軸もないのに2通りの置き方ができる組み換え可能な図形は文字通り謎の塊です。
2ピース構成のものは、現在見つかっているものでは下の2種類しかありません。
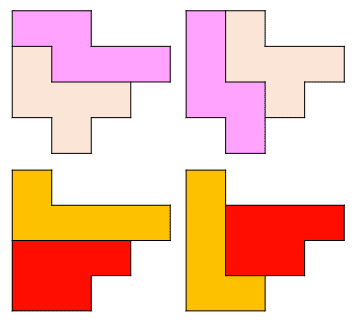
なんとなくわかるかもしれませんが、見つけるのがすごく難しいんですよ。形やピース数に一切の法則性がないわけですから、それっぽい形を見つけるたびに頭の中でピースを移動していちいち考えないといけないんです。
2ピース構成を見つけてからは、3ピース構成、4ピース構成のものも探すようになりました。
見つかったはいいが
3ピース構成のものの中で、実際に解に使用されがちなのが下の3つ。

どれも偶然に見つかったものです。他にも3ピース構成のものは数多く見つかっていますが、実際の解にはあまり使われないものが多く、あくまで理論上の概念として考えています。
2〜4ピース構成を全て合わせると、現在は24種類もの図形が見つかっています。イラストを作るのがめんどくさいのでノートの裏に覚え書きしたやつを撮ったものですがご勘弁。

それぞれどんなふうに組み換えられるのか、考えてみるのも面白いですよ。
今になって思うこと
今になって「この図形には気づかないほうが良かったのかもしれない」と思うようになってきました。2ピース構成ならまだいいのですが、4ピース構成ともなるとそれだけで図形自体がかなりの大きさを占めています。これでは実際の解に適応される例もかなり限られてきて、実用性に欠けてしまう。
また、線対称ではない以外の法則性が全くといっていいほど見つかっていないのも不安要素です。何が効いているか分からないけど、とりあえず体にいい葉っぱを医療に使っているような感じ。図形の性質としての面白みはもちろんあるのですが、解を見つけるための手段としてこれを用いるにはまだ知見が少なすぎたように感じます。
今回はここまで。結局何が言いたかったの?と聞こえてきそうですが、大丈夫。私も何を説明していたのかよくわかっていません。
いただきました、この記事、スキ0個。
それではこのへんで。
いいなと思ったら応援しよう!

