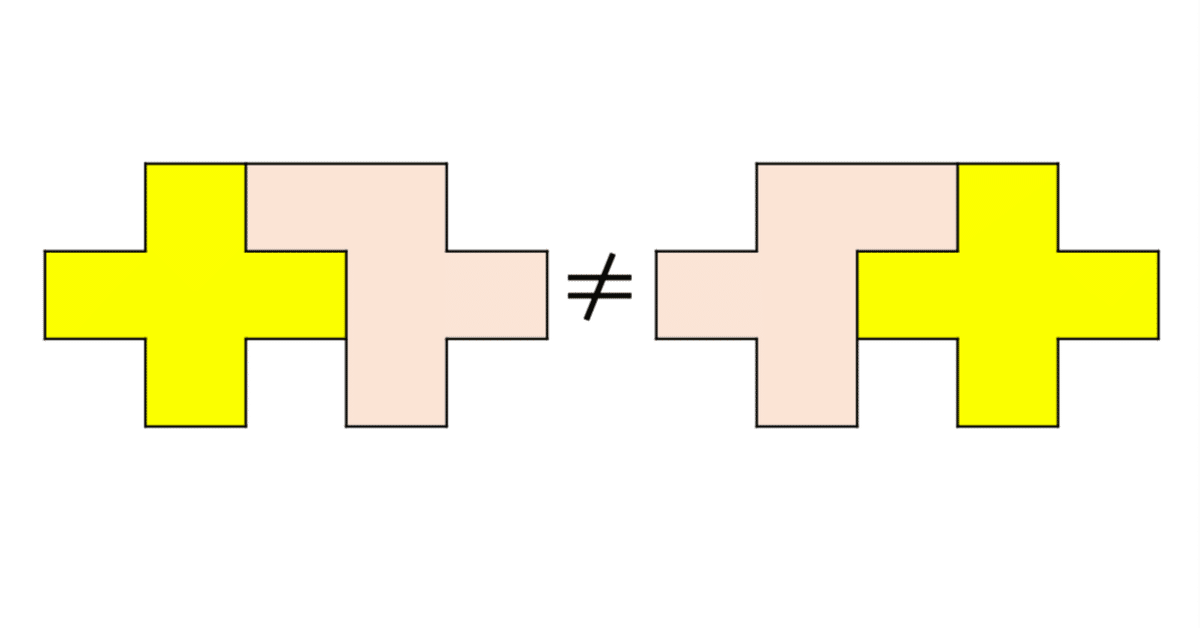
ペントミノ講座① 線対称な図形の発見
みなさんどうも、うつろです。
毎週月水金の特集記事、今日は2回目。
私がかつて傾倒していた、ペントミノパズルについてご紹介しています。
さて、初回「ペントミノパズルとの出会い」は見事0スキ。まあ内容ないので仕方ないですね。
ただピースの基礎的な説明などしているので、この記事を読まれる方は先に軽く目を通してもらった方が理解しやすいかもしれません。特に各ミノの名前とか。
今回はしっかり内容ある、つもりです。
それでは本編。
とりあえず解を見つけてみる
はじめてパズルをやった時には、ピッタリ埋めることができず挫折してしまった私。このままではいけないと、とりあえずがむしゃらにピースを当てはめて解を探し始めました。
そんな中で、だんだんキレイにプレートを埋めていくコツがわかってきました。
ピース同士には相性がある
始めてしばらく経ってわかったのですが、
「このピースとこのピース、一緒に扱うとキレイに埋まりやすいな」
と感じる組み合わせがいくつかあるんですよね。
イラストがあれば分かりやすいかな。

共通して言えるのは、「長方形に近い形になっている」ということですかね。歪な形よりもキレイに角が揃っていた方が組み込みやすいわけです。
それぞれのピースには制約がある
もう一つ、それぞれピースには置き場所に制約があることを忘れてはいけません。
一番分かりやすいのはXのミノでしょうか。このミノは唯一、形の都合でプレートの角に置くことができません。同じように、不可能というわけではありませんが、Wのミノを角に置くのもなかなか至難の業です。
一方でIのミノは、基本的にプレートの外周にしか置くことができません。もちろん内部に置いてもある程度は埋めていけるのですが、全部埋めようとするとほぼ不可能に近い。
このような制約がないものが自ずと使いやすいミノになってきます。
特に使い勝手がいいのが下の4つ。

Pのミノは、12個の中で唯一2×2の正方形が含まれている特殊な形。最後まで残していても怖くない、万能のミノです。
N、Y、Lはどれも細長い形をしているのが売り。意外と細長いミノには重宝するものです。「Iも細長いじゃん!」と思うかもしれませんが、あいつは長すぎて何かと使い勝手が悪いので除外しています。
やっと見つけた一つ目の解
こんなようなことをしばらく考えているうちに、ようやく私も記念すべき1つ目の解にありつきました。未だに基本の形としている、思い出深い解です。

これを基準にしてミノの配置を少しずつ変えることで、順調に解を見つけていった私。そんなある日、新たに見つけた解に疑問を抱きます。
同じ、ではない?
それがこちら。

初めて見つけた解と比べてみてください。ほぼほぼ同じですよね。でも内部のFとXの場所だけ違うので違う解です。一体どういうことでしょうか?
そうです、FとXでできたこの形、線対称な図形になっているんです。当時の私にとってはまさしく大発見。一気に解を見つけるスピードが上がっていきます。解を見つけた時、もしその中に線対称な図形が含まれていたら、線対称な図形だけひっくり返したものも新しい解として認めていいわけですから。
さらに私はこれと並行して、2つのミノで作れる他の線対称な図形についても合わせて探していきました。
線対称な図形 (2ピース) 全紹介
せっかくなので2ピース構成の線対称な図形を全て発表しましょう。
全て、といっても最近まで見つかっていなかったものもあるのでこれで全部かは確証が持てていません。とりあえず現段階では31種類。



解を見つけたら線対称な図形がないか自然と探すようになりました。また逆に、特定の線対称な図形を含むような解を探すということもできるわけです。
このようにここから新規の解の探索は、線対称な図形を軸に進んでいきます。
いかがだったでしょうか。線対称な図形について、ほんの少しでもわかっていただけていれば幸いです。
こんなものでは物足りないという方もいるかもしれませんがご心配なく。新要素、続々登場予定です。ぜひお楽しみに。
次回金曜日は、もう少しこの線対称について掘り下げてみようかなと思います。
それでは今日はこのへんで。
いいなと思ったら応援しよう!

