
ペントミノ講座⑤ 巨大線対称と特殊組の関係
みなさんどうも、うつろです。
相変わらずストックを作ることができていないので、この原稿は金曜日の22時半ごろから急ピッチで進めています。毎日投稿はなんとか達成したのですが、先週叶わなかった毎日2本投稿を達成するためにも、全力を尽くして今日中に記事を上げないといけない。強迫観念に攻め立てられています。
前回の記事も想像以上に好評で感動しています。フォロワーが増えた影響もあるのでしょう。今回も落胆されることのないように心がけます。
それでは本編。
巨大線対称とは?
今回のテーマは巨大線対称。文字通り巨大な線対称のことを指します。具体的には、4ピース以上で構成された線対称な図形のことです。下に2つほど例を挙げておきます。
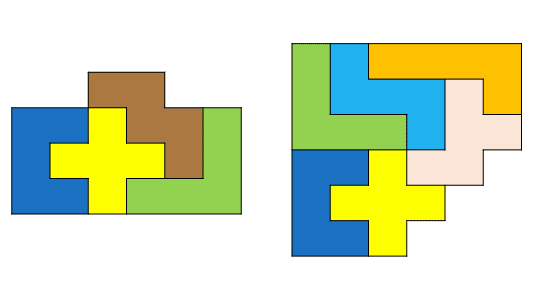
左は4ピースで構成されていますが、右は6ピース構成。全体の半分が線対称な図形に使われています。ほかに7ピース構成のものも見つかっています。そのため実際に使用している解の数は極めて少なく、実践的ではないものとなっています。見つけてしまったから泣く泣く概念として認めるしかなかったというのが正直なところですがね。
それぞれの特殊組の関わり合い
これまで紹介してきた、線対称な図形、組み換え可能な図形、入れ換え可能な図形、そして今回の巨大線対称。これらのような、解を増やすために用いることのできる特殊な図形を独自に「特殊組」と呼んでいます。そして前回の記事でも紹介しましたが、それぞれは相互に関わり合っています。
まずは下のような巨大線対称。

全体としても線対称な図形ではあるのですが、内部にXミノとFミノでできたセン対象な図形を内包しています。そのためこの巨大線対称を含む解が見つかると、全部で解は2×2=4個も見つかることになります。
下の巨大線対称についても同じように見てみましょう。
特殊組を探してみてください。

正解を発表します。FミノとNミノでできたこの形、なんか見覚えありませんか?
そう、実はこれ、2ピース構成の組み換え可能な図形なんです。
ご存じない方のために一応記事を載せておきますね。
こういうふうに長いことペントミノを見ていると、特殊組が自然と見えてくるようになります。ということで今週までの講座でみなさんの力がある程度ついていると仮定して、来週からはより実践的な内容を紹介していきたいと思っています。
今回はちょっと抜き気味。字数も1000字ちょっきりくらいでしたね。
リアクションいただけるとすごくうれしいです。
それではこのへんで。
いいなと思ったら応援しよう!

