
時系列データ解析としてのTSS その2
前回、サイクリングスポーツのトレーニングに現れるTSS (Training Stress Score)と言う数値について、その計算法をレビューした。TSSの定義式に沿って行くうちに、このTSSという数値には多少クセがある事が判明した。今回はすこしその点について掘り下げてみたい。
前回の記事
TSSは相加性を持たない
相加性:
ある対象について何かの数値を計測する際に、対象を細切れにした断片の計測値を足し上げたものが、全体についての計測値と等しくなるとき、その数値は相加性をもつと言う。
例えば、「液体の体積」とか「物質の質量」は相加性を持つ。スポーツであれば「消費カロリー」「獲得標高」「走行距離」は相加性を持つ。基本的にはアクティビティを切り分けても、つなげても、最終的に足し合わせたら、アクティビティ全体の値になるからだ。
※相加性:物理学では「示量性」とも称する。
TSSは本来的にこの相加性を持たない。パワーがおおむね一定の場合はTSSはおおむね相加性を持つし、日をまたいだ完全に独立のアクティビティについても相加性を持つかのように扱うため、(ちょうど消費カロリーと同じように)相加性を持つと感じがちである。
パワー変動がTSSに悪さする例
しかし、パワーの変動が大きいと挙動がおかしくなる。以下にこの効果が最も顕著に出るケースを示す。下図はZwiftで"Road To Sky"を登って下ったアクティビティのグラフである。データはStravaからダウンロードしてPythonで処理した(そのことについてはまたの機会に書こうと思う。)
下側のグラフの黒線がパワー、その他の線はある時刻までのデータで計算した平均パワー(緑)、NP(赤)、TSS(青、上側グラフ)である。例えば2400秒から右を紙で隠してやれば、そこでアクティビティが終わったとしたときの平均パワー、NP、TSSがいくらかを、その時刻の各線の値から読めるようになっている。
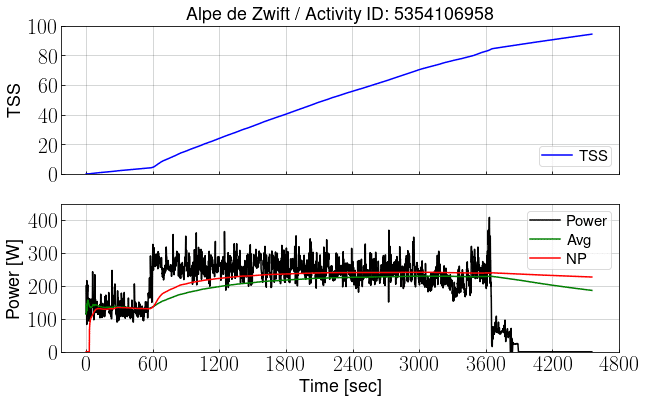
およそ3600秒で山を登り切り、その後1000秒掛けて下山している。頂上でやめていれば82程度だったTSSは、下山の間ほとんど踏んでいないにもかかわらず98まで上昇している。最初の600秒を平均130W程度で踏んでもらえたTSSは4程度だったのに、何もしなくてもTSSが16も増えてしまうのはおかしくないか?これがTSSの相加性がない、ということである。
こんなことが起こるメカニズムはというと、これは下山で踏まないでいてもNPがあまり下がらないからである。上図で平均パワーとNPの推移を見て欲しい。
平均パワー(グラフ緑色)というのは
「パワーの総和(=総投入エネルギー)」を「走行時間」で割った物
だから、あたりまえだが時間を掛ければ総投入エネルギーに戻る。つまり、下山で踏まなければ平均パワーは減少し、走行時間の延びの効果は相殺される。
これに対しNPは(Appendixで述べるが)、高パワーのデータを「優遇」するという傾向がある。そのため、低パワーで走行していても平均パワーほどは落ちてこない。しかもTSSの式はNP^2を含む
TSS = (NP / FTP)^2 x (T / 3600) x 100
から、この効果はさらに強化されてTSSに現れてしまう。
ではどうするか
もちろん理由があるから、こんなややこしい指標を採用しているのである。人間の体というのは2倍のパワーだと2倍疲れる、といったような単純なものではなく(つまり線形では無く)、高パワーではより一層の負担がある。そういう特性をちょうど良いあんばいに取り入れたいということがNPの導入動機であろう。(これはオーディオで耳の聴覚特性を補正するための関数である、ラウドネス関数に少し似ている。)
そのスポーツ生理学的な妥当性については論文などを追わなければ検証できないが、専門家ではないしそこには立ち入らない。つまり、ここでは概ねTSSの妥当性・有効性は認めるとするが、漕いでいないのにTSSが増えるということだけは我慢がならない(笑)というスタンスである。
インターバルトレーニングやスプリントなどの変動の大きいパワーを過小評価しないために導入したのに、力行していない時間帯がTSSに無用な影響を与えるというのはTSS/NPの数学的な定義のもたらす不幸である。でもこれについてはなんとかできそうな気がするので、次回以降でトライしてみる。
Appendix: Normalized Power と一般化平均
NP (Normalized Power)とは何か、にもう少し迫る。NPの計算ではパワーに対して30秒の移動平均をとったあとのパワーのデータx1, x2, ..., xiに対し以下のような「平均操作」をするのであった。(パワーのデータは1秒サンプリングであると仮定)

ここで4乗をpに置き換えた

は一般化平均と呼ばれ、ちゃんとウィキペディアの項目もある。
この一般化平均は、pをいじる事によって様々な平均を表現する事ができる万能な奴なのである。
・p=1:μ_1は普通の平均(相加平均)を与える。
・p=-1:調和平均
・p=0:計算に少し困惑するかも知れないが、p->0の極限をとると、μ_0は幾何平均(相乗平均)に収束する。
・p=2:二乗平均平方根(RMS: Root Mean Square)
このμ_pは-∞から∞の実数pで定義可能であり、面白いのがpが無限大もしくはマイナス無限大の極限をとったとき、データの最大、最小を与える。
・p -> ∞ではμ_p = max(x0, x1, ..., xn)
・p -> -∞ではμ_p = min(x0, x1, ..., xn)
なるほど、これは目からウロコであった。
このpの値を変化させて得られる平均値μ_pについて見てみる。いま、例として100個のデータの平均を取る事を考えよう。
・まず、全てのデータが同じ値xのとき、pを変えても差は出ない。括弧内はx^pになるので、μはどのpでもxになるからである。
・pによる差が出るのは変動の大きい(glitchyな)データの時である。そのようなデータを考えるために「99個の0」と「1個の100」を含むデータを考える。ただし、0をそのまま使うとpが負の時に括弧内が無限大になってしまうので、0の代わりにxを使い、あとでx->0の極限をとる。その結果が以下の通りである。

p=1の時は普通の平均なので、総和である「100」をデータ点数100で割った1が値となる。
p>1では大きな値のデータにより重みが置かれる。pが1から大きくなるにつれ値は大きくなり、100に近づいていく。NPの計算に使用されるp=4での値は31.6である。たった一個の100のデータがグンと平均をアップさせる。
p<1ではグラフではわかりにくいが、小さな値のデータにより重みが置かれる。
NPの場合、短い時間で高出力の部分をどれくらい平均で優遇するかということは、生理学的な知見を必要とするので、ここではp=4を採用した理由については論じることはできないし、論じていない。Normalizedとは「正規化」「標準化」という意味になるが、通常この言葉はデータごとの平均や変動の個体差を吸収して同じ土壌で比べるための操作を呼ぶ用語であり、「高パワーを優遇する」操作は正規化とは言わないだろう。この場合どちらかというとPhysiological Power Indexとかいった別の名前をつけた方が良さそうである。
#自転車
#ロードバイク
#ロードバイクトレーニング
#有酸素運動
#自転車ロードレース
#サイクルロードレース
#時系列
#時系列データ
#自転車トレーニング
#TSS
#時系列分析
ーーーーーーーーーーーー
続きの記事↓
