
Math Burger
このアカウントのアイコンにもなっているハンバーガーは数式を使ってデザインされています。この記事ではこの"Math Burger"がどう構成されているのかを解き明かします。
Math Burgerを構成する部品
・ バン(上)
・オニオン
・トマト
・チーズ (*)
・パティ
・レタス (*)
・バン(下)
スタンダードなチーズバーガーっすね
一般化バーガー関数 ~ Generalized Burger Function
上にあげた部品のうち(*)がついていない5つは、実はひとつの関数で表現されています。

何じゃこりゃー!と思われるかも知れないので、かいつまんで解説します。
まず、右辺の数字三つ組みは3次元空間を円柱座標で表現した物で、それぞれ半径r、回転角φ、鉛直方向の高さz、を表します。円柱座標は軸対称な形状(回転体)を記述するのに優れているんですね。

ここで最も基本となる形状として球体を表そうとすると、r-z平面内の円をφに関してぐるっと一周してやれば良いので、
S(θ,φ)=(sinθ, φ, cosθ)
という関数を考えると0<θ<2π、0<φ<2πで半径1の球体を表します(下図)。(本当は二重の球体になっているので、φは0からπまで動かすだけで球体になります)
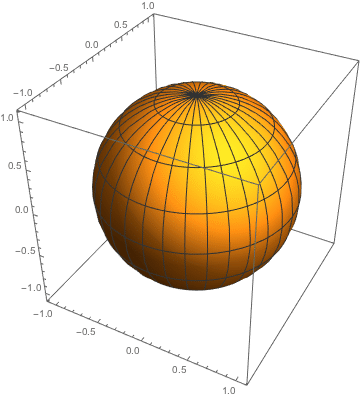
この球体をゆがめてなんとかバンズの形やオニオンの形にしたい!
いま、f(x)=xとして考えて
S(r0, θ,φ)=(sinθ, φ, f(cosθ))
と置きます。このf(x)を単なる直線からいじってやる事で球体をゆがめてやろうという作戦です。
ここで誤差関数Erf(x)と呼ばれる便利な関数を使います。この関数はx=0付近では線形(1次関数的)ですが、|x|>0.5位から頭打ちになり、|x|が大きいときは関数値が+1(または-1)に漸近するという性質があります。

ここでxはcosθであることを思い出すと、xの範囲は-1~1に限定され、その範囲の終端付近でErf(x)は頭打ちになります。つまり、先ほどの球の場合にもどって考えると、z=cosθをz=Erf(cosθ)にすることですこし縦にひしゃげる形になります。
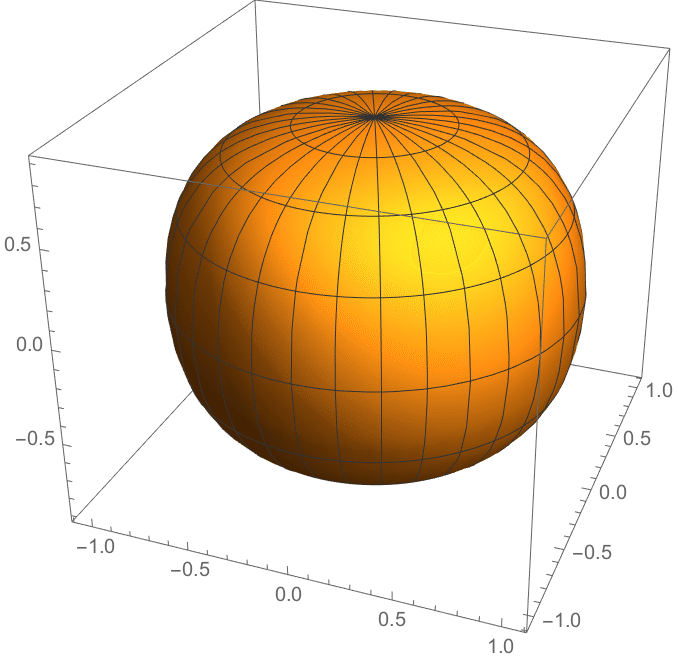
これはこれでハロウィンのカボチャのようやね。
ここで、このz=Erf(cosθ)をErf(a cosθ)といじってやり、aの値をいろいろ変えると、誤差関数が+/-1で頭打ちになるスピードをコントロールする事ができます。下図はz=Erf(a cosθ)のaを左から右へ0.1, 0.5, 1, 3と変化させた様子。aが小さいと都合上Erfの値も変動が小さくなるので縦にひしゃげますが、基本的には均等にひしゃげた球(縦に戻せば急に戻る)。aが大きいとあっという間に+/-1に張り付くため、円柱に近い形になります。

さらに、z = Erf(a (cosθ - b))とすることで、上下の非対称性も導入する事ができます。aを2に固定し、bを1, 0.5, 0と動かすとこんな感じ。上と下で頭打ちになりやすさに差が生まれます。

ここまでくるともう簡単。
z = v + w Erf(a (cosθ-b))
vは図形を上下にvだけ動かし、wは上下に均等に押しつぶす役目をします。アレ?でも

と冒頭の式とずいぶん違う気がします。大丈夫です。実は積分記号は子供だまし。誤差関数Erf(x)は実は正規分布関数でもお馴染みのガウス関数を積分して得られるんですね。

これを使えば無事

が得られます。さああとはちまちまと形状を調整して部品を調達しますよ。

数字は順番にa, b, w, v, r0を意味します
・バン(上) : B(1.2, 0.5, 0.5, 1.2, 1)
・オニオン: B(20, 0, 0.05, 0.7, 0.85)
・トマト: B(20, 0, 0.1, 0.55, 0.9)
・パティ: B(2.5, 0, 0.15, 0.3, 1)
・バン(下): B(4, -0.25, 0.15, -0.03, 0.95)
これが上バン
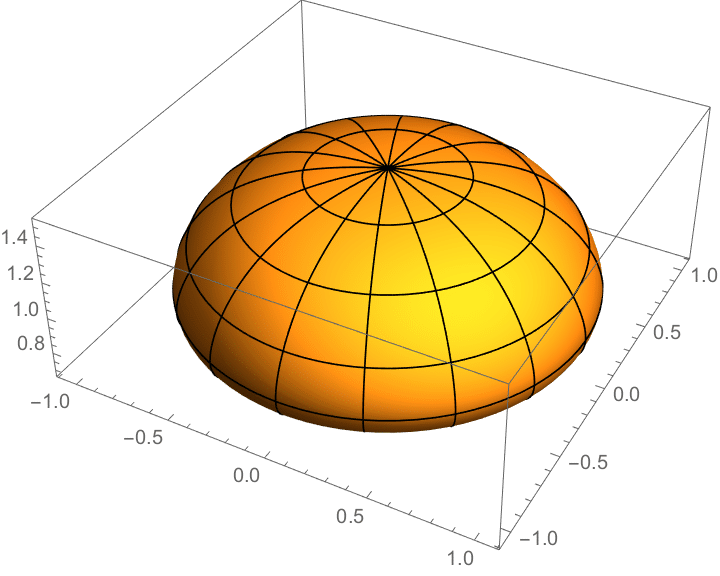
オニオン

トマト

パティ

そして下バン

バーガーの多くの部品がたったひとつの関数で表せるのが超楽しいです!
チーズ関数・レタス関数
ところでチーズとレタスはどうするのか。これらは回転対称ではないのでちょっと一筋縄ではありません。
まずチーズ関数はチーズの四角さを表現するために、(x, y, z)の直交座標にもどります。チーズのパティ上での平坦さ、パティから外れたら垂れ下がる様を表現するためになんとxとyを8乗もしなければなりませんでした
![]()

左から右へxyの2乗、4乗、6乗、8乗、10乗の場合のチーズの垂れ具合です。

レタス関数は再び円柱座標に戻り、回転にあわせて半径と高さを変動させる事でちぢれを表現します。


ここでパラメータtは0.7から1までスイープさせます。つまりtを固定するとフニャけた輪ゴムみたいな輪っかになり、その大きさがtにあわせて変化することでレタスの面になります。0.05 cos 5φの部分は半径が一回転で5回変化するように、 cos 32φは葉っぱの高さが1回転で32回波打つように、しかも半径が外に行くに従って大きく波打つようにt^8を掛けてあります。こういった変動成分を取り除くとこんな円盤になりますね。
![]()

合体して完成!
これらのパーツを合体させると、こんな感じですね。

こんなデザインのTシャツを作ってみたりもしました。

Macbook Proにも貼りました。Macがマックになっちゃう!?

Mathematicaコード
計算とプロットはMathematicaで書きました。以下がコードです。
burger[x_, a_, b_, w_, v_, r_] := w Erf[a (x - b)] + v
burgerPlot[{a_, b_, w_, v_, r_}, opt___] :=
RevolutionPlot3D[{r Sin[\[Theta]],
burger[Cos[\[Theta]], a, b, w, v, r]}, {\[Theta], 0,
2 \[Pi]}, {\[Phi], 0, \[Pi]}, opt]
meshT = Thickness[0.0025*1.5];
makePlot[part_] := Module[{},
prm = param[part];
obj[part] =
burgerPlot[prm[[1]], PlotPoints -> prm[[2]], Mesh -> prm[[3]],
PlotStyle -> prm[[4]], MeshStyle -> meshT];
]
param["bunstop"] = {{1.2, .5, .5, 1.2, 1}, {30, 10}*4, {15, 7},
Automatic};
param["onion"] = {{20, 0, .05, 0.7, .85}, {30, 10}*4, {3, 7}, White};
param["tomato"] = {{20, 0, .1, 0.55, .9}, {30, 10}*4, {3, 7}, Red};
param["patty"] = {{2.5, 0, .15, 0.3, 1}, {30, 10}*4, {15, 7}, Brown};
param["bunsbottom"] = {{4, -.25, .15, -.03, .95}, {30, 10}*4, {15, 7},
Automatic};
makePlot["bunstop"]
makePlot["onion"]
makePlot["tomato"]
makePlot["patty"]
makePlot["bunsbottom"]
sq = 0.8;
obj["cheese"] =
Plot3D[
-6 x^8 y^8 + 0.45, {x, -sq, sq}, {y, -sq, sq},
PlotStyle -> Yellow,
PlotRange -> All,
MeshStyle -> meshT,
BoundaryStyle -> meshT
];
obj["lettuce"] =
RevolutionPlot3D[
{1.05 t + 0.05 Cos[5 \[Phi]], 0.05 t^8 Cos[32 \[Phi]] + 0.17},
{t, 0.7, 1}, {\[Phi], 0, 2 \[Pi]},
PlotStyle -> Green,
PlotRange -> All,
PlotPoints -> {7, 150},
Mesh -> {7, 15},
MeshStyle -> meshT
];
Show[obj["lettuce"]]
burgerparts = {"bunstop", "onion", "tomato", "cheese", "patty",
"lettuce", "bunsbottom"};
burgerall = Map[obj, burgerparts]
g = Show[
burgerall,
PlotRange -> All,
Boxed -> False,
Axes -> False,
ViewPoint -> {4, 1, 1.5}
]
SetDirectory[NotebookDirectory[]];
Export["burger.png", g, ImageSize -> 2500]
img = Import["burger.png"]