
Pythonによる体重・体脂肪データの解析 その2 周波数領域解析編
前回はエクセルに入力したデータをPythonに取り込んでプロットを作るところまで進めました。
そのときの結果のグラフをここに再掲しておきます。

眺めているだけでもいろいろな個人的な思い出が呼び起こされて楽しいですね。赤青緑の山の一つ一つに喜怒哀楽があります。
2008年の体脂肪の急激な変化は体脂肪計の切り替えによるものです。それまでオムロンの手持ち式だったものが壊れ、タニタの乗っかる式になりました。この機種はヨドバシで片っ端から試して一番体脂肪が低く出た奴です(笑)。まあ自転車乗りは脚に筋肉が多いので、腕で測る体脂肪より脚で測る体脂肪の方が低くでるのですかね。このときは自分史上最高に自転車に乗れていた時期で、富士ヒルクライムに出場してシルバー(75分切り)を獲得できたのでした。しかもその直後にアメリカ出張があり2ヶ月測定が途絶がありましたが(図で明らかに線形補完されている部分)、帰ってきてみたらなんと体重+3kg、体脂肪+3%になっていたという笑。恐るべしアメリカ。
コロナ禍で在宅勤務になった2020/7からはZWIFTを使ったインドアサイクリングを開始し、数ヶ月で体重-5kg、体脂肪-7%の変化がありました。数値上は2008年時に近くなったとはいえ、自転車のパフォーマンスでは到底およばずで、寄る年波を感じます。あれ?よく見ると2019年の秋から体重が増え始めているので、体重増はコロナ禍のせいじゃなかったんですね。笑
閑話休題
今回はこのデータを元にして、このようなふらつきのある時系列データに対して非常に有効な周波数領域の解析法である「パワースペクトル密度推定」を行ってみたいと思います。
体重データの周波数領域解析(1) Welch法
ふらふらと乱雑な変動をしているようにみえるデータに対して、何か周期性らしきものはあるか、ふらつきの時間スケールにどのような特徴があるかといったことを明らかにするには、周波数領域解析で「パワースペクトル密度」を計算するのが最適です。表式はここには載せませんが、代わりにいくつか参考文献を挙げておきます。
小野測器さんのQ&Aページ
https://www.onosokki.co.jp/HP-WK/c_support/faq/fft_common/fft_spectrum_13.htm
パワースペクトル密度ってなんやねん、と言う話になりますが、単純に時系列データをフーリエ変換して周波数領域のスペクトルを計算すると、結果が測定時間やサンプリングレートなどに依存してしまい評価がしにくいです。
そこで「ある周波数周辺に信号の振幅パワーがどれくらいの密度であるのかな?」という値「パワースペクトル密度(PSD)」に換算します。こうすると周波数解像度が変わっても値が維持されます。また、「パワー」という言葉を使うのは信号の振幅が持つエネルギーを「毎秒あたりのエネルギー」(=パワー)に換算するからです。
元の信号の単位がXだとすると、PSDの単位はX^2/Hzになります。元の信号の振幅をa倍にすると、パワーの表現であるPSDはa^2倍になり、何かと直観的に把握しづらいところがあるので、PSDの平方根である振幅スペクトル密度(ASD)が使われる事も一般的です。この場合ASDの単位はX/√Hzという風変わりなものになります。
対象とする時系列データは乱雑で統計的なものであるため、定義上は無限の時間測定したとき初めて真のPSD/ASDが得られることになります。それは実用上不可能なので、有限時間の測定でPSDを求めます。これ「パワースペクトル密度推定」といいます。
パワースペクトル密度の推定にはWelch法がオススメです。Welch法は、時系列データを所定の長さに切って、それぞれについて計算したPSDの平均を取るというものです。Pythonではscipy.signalライブラリに含まれるwelch関数、MatlabならSignal Processing Toolboxに含まれるpwelchを使用します。
from scipy import signal
data_len=len(y)
nfft = 2**11;
freq, Wxx = signal.welch(df['weight'], 1, 'hanning', noverlap = nfft/2, nperseg=nfft, detrend='linear')welch関数の引数は順番に、時系列データ、サンプリング周波数、窓関数で、この例ではオプションとしてオーバーラップするデータの個数、データ点数、トレンド除去の方法を指定しています。
今回の例ではサンプリングレートは1日なので、サンプリング周波数は1 [1/day]です。サンプリング周波数として引数では1を与え、代わりに結果のHzを1/dayと読み替える事にします。
窓関数にはhanning窓を使用します。窓関数に必要性についてはウィキペディアを参照。
窓関数を使用すると、前後部のデータを減衰させてFFTに渡すことになるので、値を一部「捨てる」ことになります。hanning窓の場合、解析するデータセグメントをセグメント長の半分ずつ重複して解析する事で、前のセグメントで捨てた分を次のセグメントで拾うことができ、データ点の価値を極力無駄なく、また重複も無く使用する事ができます。ということで50%オーバーラップさせて処理させます。
各データセグメントでは窓関数に加え、トレンド除去することでデータセグメントの先頭と最後尾の「段差」の影響を抑えます。ここではデータの平均と線形トレンドを除去する'linear'を採用。
返り値は周波数軸とPSDです。
体重データの周波数領域解析(2) 結果のプロット
ということで、PSDの平方根(つまりASD)をプロットしたものが次の図です。

赤が振幅スペクトル密度(ASD)で濃い赤が下で説明する二乗平均平方根(RMS)です。周波数がHzの代わりに1/dayの単位になるのでASDはkg/√Hzの代わりにkg/√1/dayの単位になります。
ASDは概ね1/√f(つまりPSDで1/f)の特徴を持つ1/fゆらぎを示しました。
驚くべきことに周期1週間とその3倍波にピークが出現しました。
ここでRMSについて説明しておきます。RMSは時系列データを二乗して平均を取ったものの平方根で、時系列データが平均ゼロの場合を考えれば標準偏差に相当する量です。パーセバルの定理によるとパワースペクトル密度を周波数で積分したものは信号の二乗積分を時間平均したものと一致します。
つまり上の図で言うと赤い線(ASD)を二乗したもの(つまりPSD)を全周波数で積分し、平方根を取るとRMSが得られるという事です。

とすると、どの周波数がどれだけRMSに貢献しているか知りたくなるのが人情です。このときASDは低周波ほど大きくなるのが世の常ですので、成分を下から上ではなく上から下に計算する事にして、ある周波数fより上の周波数の成分がどれだけのRMSになるのかを計算します。

これが上手の濃い赤線RMSです。左軸の数値を共有しますが単位はkg_rmsとなります。
bw=freq[1]-freq[0]
Wrms = np.sqrt(np.flip(np.cumsum(np.flip(Wxx))))*np.sqrt(bw)RMSを見ると、1年より速い変動では体重は0.7kg_rmsです。これは正弦波換算で+/-1kg程度、正規分布換算なら+/-2σでいって+/-1.4kgに95%の確率でおさまる、という感じになります。感覚的にはそんなにおかしくなさそうです。これよりゆっくりの変動はdetrendの影響とかも出てくるのでPSDで見るのには向かないでしょう。
1週と1/3週のピークについて、RMSのカーブで見ると、ほとんど寄与がないので、時系列信号では到底観測不可能でしょう。このような微弱な周期性も検出できるのが周波数領域解析の力です。ちなみにそれぞれのピークについて頂点の値と両隣を取り出してRMSへの寄与を計算すると
idx=np.argmin(np.abs(freq-3/7))
np.sqrt(np.sum(Wxx[(idx-1):(idx-1)+3]*bw))
idx=np.argmin(np.abs(freq-1/7))
np.sqrt(np.sum(Wxx[(idx-1):(idx-1)+3]*bw))1/3週が0.042 kg_rmsと1週と0.090kg_rmsとなりました。1週間での体重の周期性は正弦波換算で+/-0.13kg程度です。いやー、時系列では全く見えなくて当然ですね。
体重データの周波数領域解析(3) 結果の考察
データ解析で大事なことは、結果をうのみにせず吟味することです。まずASDの大半を占める1/fゆらぎについて。これは出張前後の体重の段差や運動による急激な体重減少の影響では無いかと言う懸念がありますが、それもふくめて体重変動の特徴と思うこともできますので、この結果は受容して良いかと思います。
1週間・1/3週間周期の変動成分ですが、これは測定方法によるartifactである可能性がまだ排除できません。例えばデータ欠損を線形補間で埋めていますが、欠損がたとえば週末に偏っている等の場合に、本来乱雑であるデータをなめらかにつないでいる事がこの周期性の原因になっていないか?という懸念もあります。これについては人工的なデータでシミュレーションテストしてみる事ができそうです。(これについては次のnoteで取り扱った。)
測定点どうしに測定毎に独立な誤差が加わる場合、それは周波数依存性のないホワイトノイズとして現れます。測定結果がそうなっていないという事は、測定が体重計の統計的な誤差で制限されていないということを示唆します。仮に、測定が過去の測定値に引きずられてしまう、もしくはゆっくりと変動する環境変動に引きずられる、と言う事があれば今回見られたような周波数依存性を持つスペクトルを示すという可能性はあるでしょう。この点については検証できていません。これは、例えば毎回の測定毎に60kgのダンベルで(もしくはせめて5kgのダンベルを持って)、体重計を校正するなど、追加の情報が必要ですが、さすがに煩雑すぎますね。
体脂肪率データの周波数領域解析(1) プロット
体脂肪率についても同様に処理します。今度は風呂前と風呂後の2本のデータがあるので、色を変えてプロットします。

体脂肪率%のASDですので単位は%/√1/day、RMSの単位は%rmsとなります。ここでも横軸の値は共有していますが異なる量を表示している事に注意してください。
ここでもASDはおおむね1/√fのスロープを持ち、また1週間周期に小さなピークを持っています。なんとなく1年周期の変動があるっぽいところも興味深いです。そして、風呂に入る前と入った後でASDに差がある点が興味深いです。この差は歴然としており、風呂前で全体域で1.5%程度のRMS、風呂後のデータで1%程度のRMSになっています。周波数に寄らず全帯域で1.5~1.6倍の差ですので結構大きいです。
体脂肪率データの周波数領域解析(2)
そこで風呂にはいる前後でどれだけ体脂肪率の測定値が変化するかを評価します。以下は体脂肪率(風呂前)から体脂肪率(風呂後)を差し引いたものの時系列をプロットしたものです。濃い紫が生データ、マゼンタが28日移動平均。

まず、風呂前の方が絶対値が高く出る傾向があります。とくに手持ち式の体脂肪計を使っていた2008年までで顕著です。またこの2008年までは強い季節性の変動も見られます。これは怪しいですね。
今度は周波数領域で解析してみます。2つの時系列データの差動成分のスペクトルを見る事で相関する成分を除去し、非相関成分を強調した解析をする事ができます。
全体のスペクトルが1/fよりもずっとフラットということに気づきますが、測定の統計誤差(つまりこの場合誤差の大きい方=風呂前のデータ)を示唆しているかも知れません。そして、1年周期にピークが出ています。このピークがもつRMSは0.33%_rmsほどですので、1年周期の正弦波にすれば+/-0.5%に相当するようなものです。なかなかデカい。
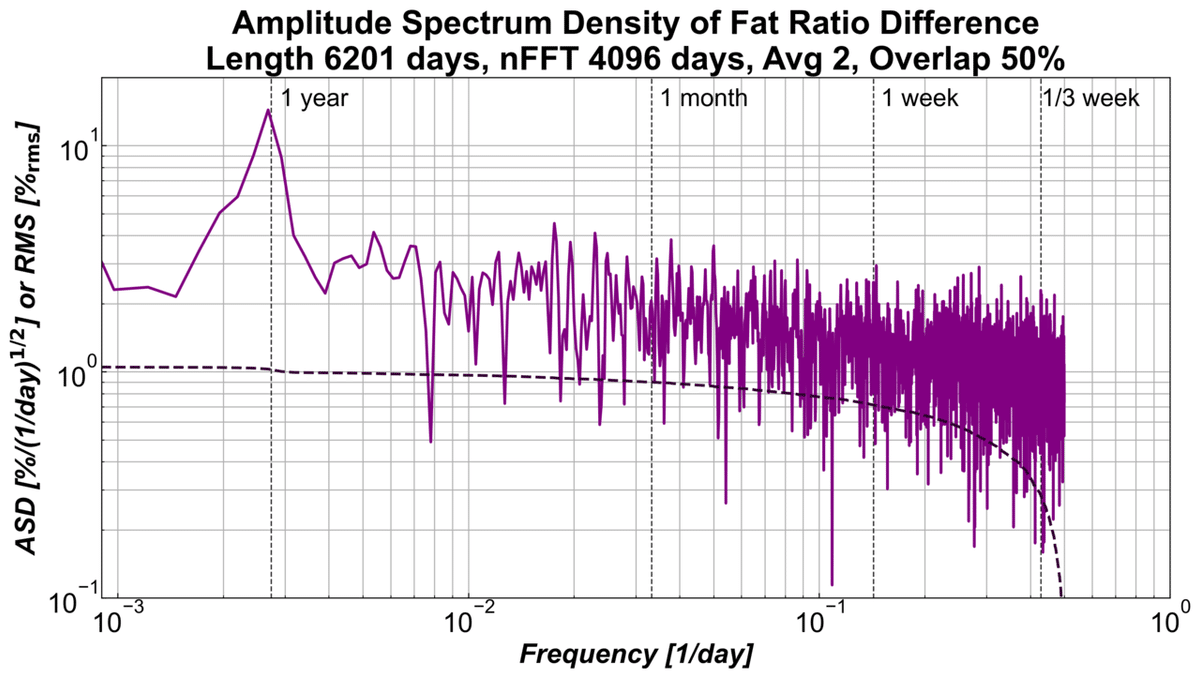
これは私の仮説ですが、皮膚が乾燥して体脂肪が高く出ることがこの周期性の原因なのではないでしょうか。とくにこれは手持ちの体脂肪計で顕著だったようです。体脂肪計を換えてからは影響は少なくなったようですし、現在の居住地では年中湿度が安定しているので、その傾向が小さくなっているようにも思えます。しかし、パワースペクトルを見る限り、風呂の後に測定したデータの方が変動が少なく安定していると言えますので、今後は風呂後のデータのみを見ればいいのかとも思います。
17年もやっていますが、よくよくデータを観察すれば、まだ新しい事が分かるものですね。
まとめ
以上見たように周波数領域でのパワースペクトル密度の解析は時系列では見えないような情報も明らかにしてくれる非常にパワフルなツールで、おもに定常的な信号の解析につかいます。最近はスマホでも音声はもとより振動やらの時系列データも取得できるようですので、アイデア次第で様々なことができそうですね。例えば、自転車の空気圧を変えて走行して振動データを集めるとか…。
Appendix
コードをまとめて載せておきます。体重の解析とプロットに使ったコード
from scipy import signal
data_len=len(df)
nfft = 2**11;
freq, Wxx = signal.welch(df['weight'], 1, 'hanning', noverlap = nfft/2, nperseg=nfft, detrend='linear')
bw=freq[1]-freq[0]
Wrms = np.sqrt(np.flip(np.cumsum(np.flip(Wxx))))*np.sqrt(bw)
fig, ax = plt.subplots(1,1,figsize=(14, 7))
vline_range=[1e-6,1e2]
vline_col=[0.2,0.2,0.2]
vline_list=[1/7,3/7,1/30,1/365]
for val in vline_list:
ax.loglog([val,val], vline_range, '--', color=vline_col, linewidth=1)
ax.loglog(freq,np.sqrt(Wxx),'r-',linewidth=2,label='ASD')
ax.loglog(freq,Wrms,'--',color=[0.5,0,0],linewidth=2,label='RMS')
fontspec1={'fontweight': 'bold','fontstyle': 'italic'}
fontspec2={'fontweight': 'bold'}
ax.set_xlabel('Frequency [1/day]', fontdict=fontspec1)
ax.set_ylabel('ASD [kg/(1/day)$\mathbf{^{1/2}}$] or RMS [kg$_\mathbf{rms}$]', fontdict=fontspec1)
ax.set_xlim([0.0009,1])
ax.set_ylim([1e-1,20])
ylim=ax.get_ylim()
text_list = ['1/3 week','1 week','1 month','1 year']
pos_list = [0.43,0.15,0.035,0.0029]
for ii in range(len(text_list)):
ax.text(pos_list[ii], ylim[1]*0.75, text_list[ii], fontsize=18);
title_txt=('Amplitude Spectrum Density of Weight\n'+
'Length {len:d} days, nFFT {nfft:d} days, '+
'Avg {avg:d}, Overlap 50%')
ax.legend()
ax.set_title(title_txt.format(len=data_len,nfft=nfft,avg=np.int(data_len/(nfft/2))-1), fontdict=fontspec2)
plt.savefig('./weight_asd.pdf', bbox_inches='tight')
plt.savefig('./weight_asd.png', bbox_inches='tight')体脂肪率の解析とプロットに使ったコード
nfft = 2**11;
freq, Pxx = signal.welch(df['fat_before'], 1, 'hanning', noverlap = nfft/2, nperseg=nfft, detrend='linear')
freq, Qxx = signal.welch(df['fat_after'], 1, 'hanning', noverlap = nfft/2, nperseg=nfft, detrend='linear')
bw=freq[1]-freq[0]
Prms = np.sqrt(np.flip(np.cumsum(np.flip(Pxx))))*np.sqrt(bw)
Qrms = np.sqrt(np.flip(np.cumsum(np.flip(Qxx))))*np.sqrt(bw)
fig, ax = plt.subplots(1,1,figsize=(14, 7))
vline_range=[1e-6,1e2]
vline_col=[0.2,0.2,0.2]
vline_list=[1/7,3/7,1/30,1/365]
for val in vline_list:
ax.loglog([val,val], vline_range, '--', color=vline_col, linewidth=1)
ax.loglog(freq,np.sqrt(Pxx),'b-',linewidth=2,label='Before ASD')
ax.loglog(freq,np.sqrt(Qxx),'-',color=[0,.7,0],linewidth=2,label='After ASD')
ax.loglog(freq,Prms,'--',color=[0,0,0.5],linewidth=2,label='Before RMS')
ax.loglog(freq,Qrms,'--',color=[0,0.3,0],linewidth=2,label='After RMS')
fontspec1={'fontweight': 'bold','fontstyle': 'italic'}
fontspec2={'fontweight': 'bold'}
ax.set_xlabel('Frequency [1/day]', fontdict=fontspec1)
ax.set_ylabel('ASD [%/(1/day)$\mathbf{^{1/2}}$] or RMS [%$_\mathbf{rms}$]', fontdict=fontspec1)
ax.set_xlim([0.0009,1])
ax.set_ylim([1e-1,30]);
ylim=ax.get_ylim()
text_list = ['1/3 week','1 week','1 month','1 year']
pos_list = [0.43,0.15,0.035,0.0029]
for ii in range(len(text_list)):
ax.text(pos_list[ii], ylim[1]*0.75, text_list[ii], fontsize=18);
title_txt=('Amplitude Spectrum Density of Fat Ratio\n'+
'Length {len:d} days, nFFT {nfft:d} days, '+
'Avg {avg:d}, Overlap 50%')
ax.set_title(title_txt.format(len=data_len,nfft=nfft,avg=np.int(data_len/(nfft/2))-1),
fontdict=fontspec2)
ax.legend(ncol=2)
plt.savefig('./fat_asd.pdf', bbox_inches='tight')
plt.savefig('./fat_asd.png', bbox_inches='tight')体脂肪率の差の解析とプロットに使ったコード
dfat=(df['fat_before']-df['fat_after'])
nfft = 2**12;
freq, Dxx = signal.welch(dfat, 1, 'hanning', noverlap = nfft/2, nperseg=nfft, detrend='linear')
bw=freq[1]-freq[0]
Drms = np.sqrt(np.flip(np.cumsum(np.flip(Dxx))))*np.sqrt(bw)fig, ax1 = plt.subplots(1,1,figsize=(14, 5))
dfat.plot(ax=ax1,color=[0.5,0,0.5])
dfat.rolling(window=28).mean().plot(ax=ax1,color=[1,0,1])
ax1.set_ylim([-4,6])
ax1.set_ylabel('delta(Fat Ratio) [%]', fontdict={'fontweight': 'bold','fontstyle': 'italic'})
ax1.yaxis.set_minor_locator(MultipleLocator(.5))
start_date = '2004/07/01'
end_date = '2022/01/01'
x_start_date = datetime.datetime.strptime(start_date,'%Y/%m/%d')
x_end_date = datetime.datetime.strptime(end_date,'%Y/%m/%d')
ax1.set_xticks(np.arange(0,1e4,1e3))
ax1.set_xticklabels(np.arange(0,1e4,1e3), fontdict={'fontstyle': 'italic'})
ax1.set_xlim([x_start_date,x_end_date])
ax1.set_title('Fat Ratio(Before Bath) - Fat Ratio(After Bath)', fontdict={'fontweight': 'bold'})
# Major ticks every 6 months.
fmt_half_year = mdates.MonthLocator(interval=6)
ax1.xaxis.set_major_locator(fmt_half_year)
# Minor ticks every month.
fmt_month = mdates.MonthLocator()
ax1.xaxis.set_minor_locator(fmt_month)
#locs = ax1.get_xticks()
ax1.tick_params(axis='x',labelrotation=90)
ax1.xaxis.set_major_formatter(mdates.DateFormatter('%Y/%-m'))
ax1.set_xlabel(None)
ax1.grid(b=True, which='major', color=[0.4,0.4,0.4], linestyle='-')
ax1.grid(b=True, which='minor', color=[0.8,0.8,0.8], linestyle='-')
plt.savefig('./dfat.pdf', bbox_inches='tight')
plt.savefig('./dfat.png', bbox_inches='tight')fig, ax = plt.subplots(1,1,figsize=(14, 7))
vline_range=[1e-6,1e2]
vline_col=[0.2,0.2,0.2]
vline_list=[1/7,3/7,1/30,1/365]
for val in vline_list:
ax.loglog([val,val], vline_range, '--', color=vline_col, linewidth=1)
ax.loglog(freq,np.sqrt(Dxx),'-',color=[0.5,0,0.5],linewidth=2)
ax.loglog(freq,Drms,'--',color=[0.2,0,0.2],linewidth=2)
fontspec1={'fontweight': 'bold','fontstyle': 'italic'}
fontspec2={'fontweight': 'bold'}
ax.set_xlabel('Frequency [1/day]', fontdict=fontspec1)
ax.set_ylabel('ASD [%/(1/day)$\mathbf{^{1/2}}$] or RMS [%$_\mathbf{rms}$]', fontdict=fontspec1)
ax.set_xlim([0.0009,1])
ax.set_ylim([1e-1,20]);
ylim=ax.get_ylim()
text_list = ['1/3 week','1 week','1 month','1 year']
pos_list = [0.43,0.15,0.035,0.0029]
for ii in range(len(text_list)):
ax.text(pos_list[ii], ylim[1]*0.75, text_list[ii], fontsize=18);
title_txt=('Amplitude Spectrum Density of Fat Ratio Difference\n'+
'Length {len:d} days, nFFT {nfft:d} days, '+
'Avg {avg:d}, Overlap 50%')
ax.set_title(title_txt.format(len=data_len,nfft=nfft,avg=np.int(data_len/(nfft/2))-1),
fontdict=fontspec2)
plt.savefig('./dfat_asd.pdf', bbox_inches='tight')
plt.savefig('./dfat_asd.png', bbox_inches='tight') #時系列 #時系列データ #周波数領域 #スペクトル分析 #データ解析 #データ可視化 #体重 #体脂肪 #Python3 #matplotlib
