
乗法公式を使いこなそう⑥基本形の乗法公式の分類-分類の流れと具体例-
基本形の乗法公式は、右辺の$${ x}$$を含む項の有無から、
$${(x+a)(x+b)=x^2+(a+b)x+ab}$$
$${ (x \pm a)^2=x^2 \pm 2ax+a^2}$$
と、
$${ (x+a)(x-a)=x^2-a^2}$$
に分けることができ、この分け方を分類1と呼びます。
次に、右辺の定数項が2乗した数かどうかから、
$${(x+a)(x+b)=x^2+(a+b)x+ab}$$
と、
$${ (x \pm a)^2=x^2 \pm 2ax+a^2}$$
$${ (x+a)(x-a)=x^2-a^2}$$
に分けることができ、この分け方を分類2と呼びます。
最後に、右辺の$${ x}$$の係数の符合から、
$${ (x+a)^2=x^2+2ax+a^2}$$
と、
$${ (x-a)^2=x^2-2ax+a^2}$$
に分けることができ、この分け方を分類3と呼びます。
これらの分類を使うと、因数分解をするときに、どの基本形の乗法公式を使うことができるか、わかりやすくなります。
今回は、分類の使い方の流れを具体例として、
$${x^2+12x+36}$$
を使って、フローチャートを作りまとめます。
また、作ったフローチャートを使い例題として、$${x^2-49}$$
$${x^2+5x+6}$$
$${x^2-6x+9}$$
$${x^2-20x+36}$$
の因数分解をしてみましょう。
今回のフローチャートでは、基本形の乗法公式を使って必ず因数分解をすることができる二次式を考えています。
使い方の流れ
分類を使って、
$${x^2+12x+36}$$
の因数分解をしながら、フローチャートを作っていきましょう。
またフローチャートでは、簡略した表記を使いたいと思います。
この式の因数分解をしながら、簡略表記についても書いていきます。
以下では基本形の乗法公式、
$${(x+a)(x+b)=x^2+(a+b)x+ab}$$
を公式1、
$${ (x \pm a)^2=x^2 \pm 2ax+a^2}$$
を公式2、
$${ (x+a)(x-a)=x^2-a^2}$$
を公式3と簡略表記します。
また、
$${ (x+a)^2=x^2+2ax+a^2}$$
を公式2+、
$${ (x-a)^2=x^2-2ax+a^2}$$
を公式2-と簡略表記します。
流れ1
$${x^2+12x+36}$$
は$${ x}$$を含む項が有るので分類1より、
$${(x+a)(x+b)=x^2+(a+b)x+ab}$$
$${ (x \pm a)^2=x^2 \pm 2ax+a^2}$$
の公式1または公式2のどちらかを使うことができると決まります。
以下では分類1の結果、$${ x}$$を含む項が有る場合を有、$${ x}$$を含む項が無い場合を無と簡略表記します。
ここで分類1で無の場合は、
$${ (x+a)(x-a)=x^2-a^2}$$
の公式3を使うことができると決まります。
$${x^2+12x+36}$$
の場合は、分類1の結果は有となり、公式1または公式2のどちらかを使うことができると決まります。
ここまででフローチャートは、

のようになります。
流れ2
ここまでで、
$${x^2+12x+36}$$
は分類1で有なので、公式1または公式2を使うことができると決まっています。
この式は、定数項が2乗した数になっているので分類2より、
$${(x+a)(x+b)=x^2+(a+b)x+ab}$$
$${ (x \pm a)^2=x^2 \pm 2ax+a^2}$$
の公式1または公式2のどちらかを使うことができると決まります。
以下では分類2の結果、定数項が2乗した数になっている場合をYes、定数項が2乗した数になっていない場合をNoと簡略表記します。
ここで分類2でNoの場合は、
$${(x+a)(x+b)=x^2+(a+b)x+ab}$$
の公式1を使うことができると決まります。
$${x^2+12x+36}$$
の場合は、分類2の結果はYesとなり、公式1または公式2のどちらかを使うことができると決まります。
ここまででフローチャートは、

のようになります。
流れ3
ここまでで、
$${x^2+12x+36}$$
は分類1で有、分類2でYesなので、公式1または公式2を使うことができると決まっています。
このときは、
$${ (x \pm a)^2=x^2 \pm 2ax+a^2}$$
をまずは使うことができると考えて試しに因数分解をし、$${ x}$$を含む項の係数のみを計算します。
つまり、
$${x^2+12x+36=(x \pm 6)^2}$$
と試しに因数分解をし、
$${ \pm 2 \times 6=\pm 12}$$
と$${ x}$$を含む項の係数のみを計算します。
この$${ \pm 12}$$の絶対値$${ 12}$$と、左辺の$${ x}$$を含む項の係数$${ +12}$$の絶対値$${ 12}$$を比較し、同じになるか確認をします。
この場合は同じになるので、
$${ (x \pm a)^2=x^2 \pm 2ax+a^2}$$
の公式2を使うことができると決まります。
以下では、試しに因数分解をすることから確認までを実験と簡略表記します。
また実験をし、同じになる場合をOK、同じにならない場合をNGと簡略表記します。
ここで実験でNGの場合は、
$${(x+a)(x+b)=x^2+(a+b)x+ab}$$
の公式1を使うことができると決まります。
$${x^2+12x+36}$$
の場合は、実験の結果はOKとなり、公式2を使うことができると決まります。
ここまででフローチャートは、

のようになります。
流れ4
ここまでで、
$${x^2+12x+36}$$
は分類1で有、分類2でYes、実験でOKなので、公式2を使うことができると決まっています。
この式は、$${ x}$$の係数の符合がプラスになっているので分類3より、
$${ (x+a)^2=x^2+2ax+a^2}$$
の公式2+を使うことができると決まります。
以下では分類3の結果、$${ x}$$の係数の符合がプラスになっている場合を+、$${ x}$$の係数の符合がマイナスになっている場合を-と簡略表記します。
ここで分類3で-の場合は、
$${ (x-a)^2=x^2-2ax+a^2}$$
の公式2-を使うことができると決まります。
$${x^2+12x+36}$$
の場合は、分類3の結果は+となり、公式2+を使うことができると決まります。
ここまででフローチャートは、
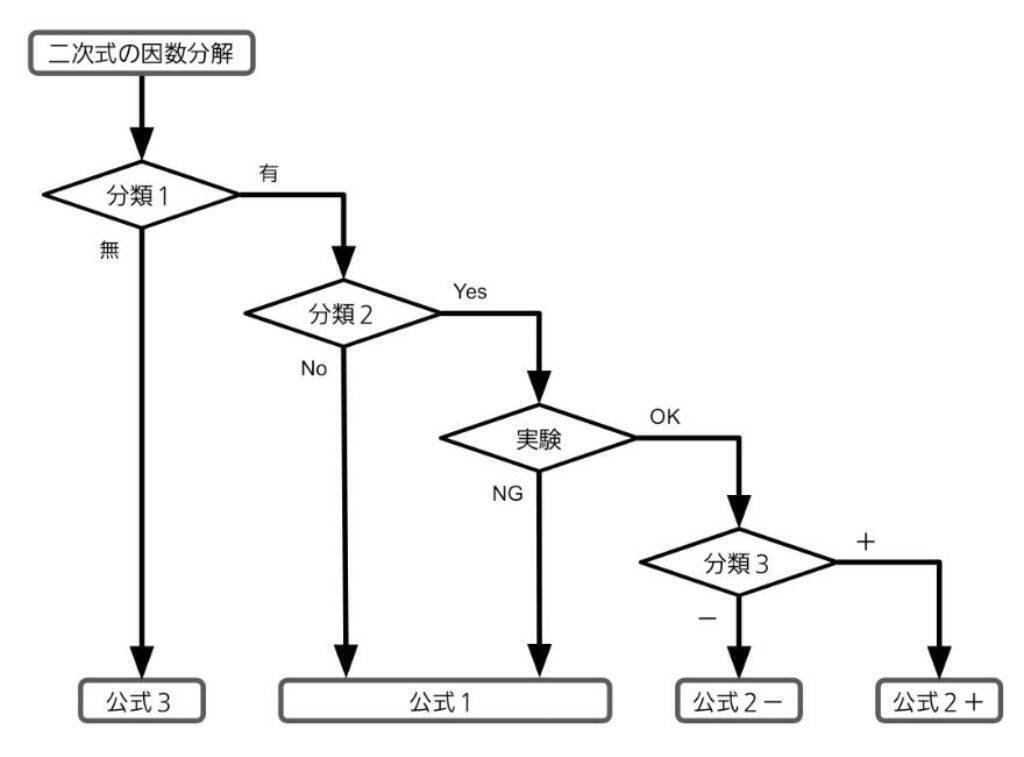
のようになり、これで完成となります。
例題
完成したフローチャートを使って、
$${x^2-49}$$
$${x^2+5x+6}$$
$${x^2-6x+9}$$
$${x^2-20x+36}$$
の因数分解をしてみましょう。
1式の場合
$${x^2-49}$$
の因数分解はフローチャート、

の赤線で示したルートになるので、
$${ (x+a)(x-a)=x^2-a^2}$$
の公式3を使い、
$${x^2-49=(x+7)(x-7)}$$
となります。
2式の場合
$${x^2+5x+6}$$
の因数分解はフローチャート、
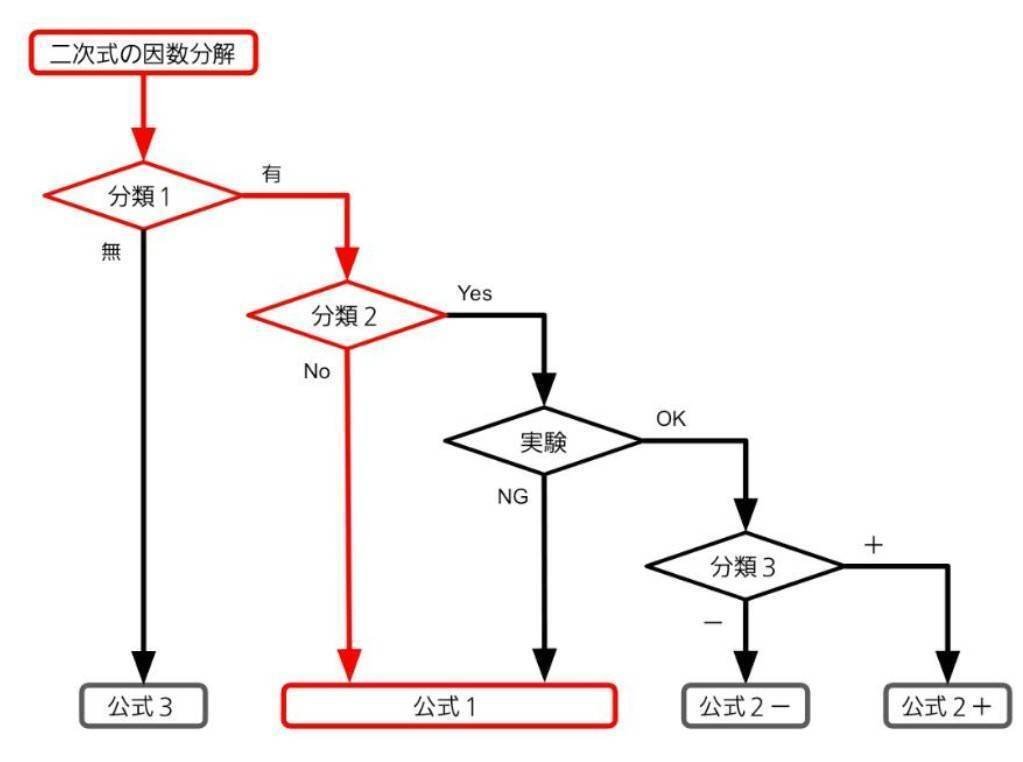
の赤線で示したルートになるので、
$${(x+a)(x+b)=x^2+(a+b)x+ab}$$
の公式1を使い、
$${x^2+5x+6=(x+2)(x+3)}$$
となります。
3式の場合
$${x^2-6x+9}$$
の因数分解はフローチャート、

の赤線で示したルートになるので、
$${ (x-a)^2=x^2-2ax+a^2}$$
の公式2-を使い、
$${x^2-6x+9=(x-3)^2}$$
となります。
4式の場合
$${x^2-20x+36}$$
の因数分解はフローチャート、

の赤線で示したルートになるので、
$${(x+a)(x+b)=x^2+(a+b)x+ab}$$
の公式1を使い、
$${x^2-20x+36=(x-2)(x-18)}$$
となります。
まとめ
今回は、基本形の乗法公式を使った因数分解について、分類の使い方の流れをフローチャートを作りまとめました。
また、完成したフローチャートを使った具体例として、4問の因数分解をしました。
このフローチャートのような流れを知っておくと、因数分解でどの基本形の乗法公式を使うことができるかわかりやすくなります。
これにより、因数分解が簡単にできるようになると思います。
因数分解が苦手、速くできないという場合は、今回のようなフローチャートを使ってみてください。
また、文字を多く含む式の因数分解が苦手な場合も、このフローチャートのような流れを意識してみてください。
因数分解がやりやすくなると思います。
