
Tableau数学 - 2. Projection view : 投影図
こんにちは、おつうです。今年も参加させて頂きました、Tableau Tips * Tabjo Advent Calendar 2023では、Tableau数学の第2弾を執筆してみようと思います。
さて今回は、先日のMoM2023W41で使った「投影図」について、オリジナルであるさかぴーさんへのリスペクトも込めて、数学の考え方から説明してみます。
Viz for #MoM2023 | Week41 What are Retail Investors Interested in Buying in 2023?https://t.co/c2Puvnh0La
— おつう (@tsu_chaan) November 6, 2023
Projection view of simple bar chart.
thanks :@VizWizBI
Inspiration : @unbosoms viz : https://t.co/iarEvmzcon #makeovermonday pic.twitter.com/pm10fXcOE0
はじめに
今回の投影図を理解するにあたって、重要なキーワードはベクトルと行列です。多くの大学生は線形代数として履修します。これを基礎からすべて説明するのは時間がかかるので、「Tableauの計算フィールドで何をしているのかを、なんとなく理解して使いこなす」ことをこのNoteのゴールにしたいと思います。とは言いつつも、Tableau数学では最低限の数学の知識は、しっかりと説明することをモットーにしてますので、是非お付き合いください。
ベクトルと行列
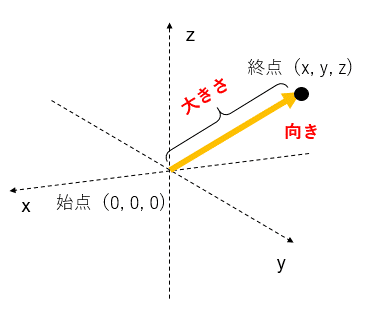
ベクトルとは、数を一列に並べたものです。ベクトルは大きさと向きの2つの要素を持ちます。イメージしやすくするために、3次元空間を考えます。原点に始点を置いたとき、任意の点までの距離が大きさであり、矢印の方向が向きになります。このベクトルを数学では以下のように記述します。これが行列です。
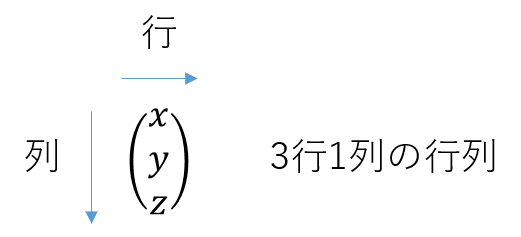
行列とは、数を縦と横に並べたものです。先ほどはベクトルを行列で表したので1列しかありませんでしたが、以下のような行列も存在します。

行列の演算規則と一次変換
今回は、行列の積(掛け算)について説明します。これは、ルールとして覚えてもらうしかありません。

まず、青い線を見て下さい。計算結果の1行目は、1行目と1列目を順番にかけたものを足すことで得られます。次に2行目は、赤い線で示した2行目と1列目の積の和です。具体的な数字を代入すると、イメージしやすいはずです。

そもそも、なぜベクトルを行列で表現したのかというと、計算しやすくするためです。そして、行列の積を計算することにより、新しいベクトルが得られることが分かりました。これが、ベクトルの一次変換であり、線形代数の醍醐味でもあります。つまり、行列とは「ベクトルの別のベクトルに変換するもの」です。

一次変換が図形的にイメージしやすくなる動画を見つけました。このように、元のベクトルを自由に変換することで、新しいベクトル、つまり今回であれば投影図を計算するわけです。

投影図
さて、漸く本題です。今回は、投影図を作ります。先に述べてきたベクトルの一次変換を使うわけですが、コチラを参考にさせて頂きました。スクリーンに投影された新しい座標を、どのように計算するかが解説されています。理解したい計算式は以下です。

難しいことに変わりはありませんが、これまでの説明もあって、
1. 3行3列型の行列である
2. ベクトルの一次変換を2回している?
ということが、なんとなくの分かるのではないでしょうか。ここからは、どのような変換をしているのか、なるべくわかりやすく解説してみます。
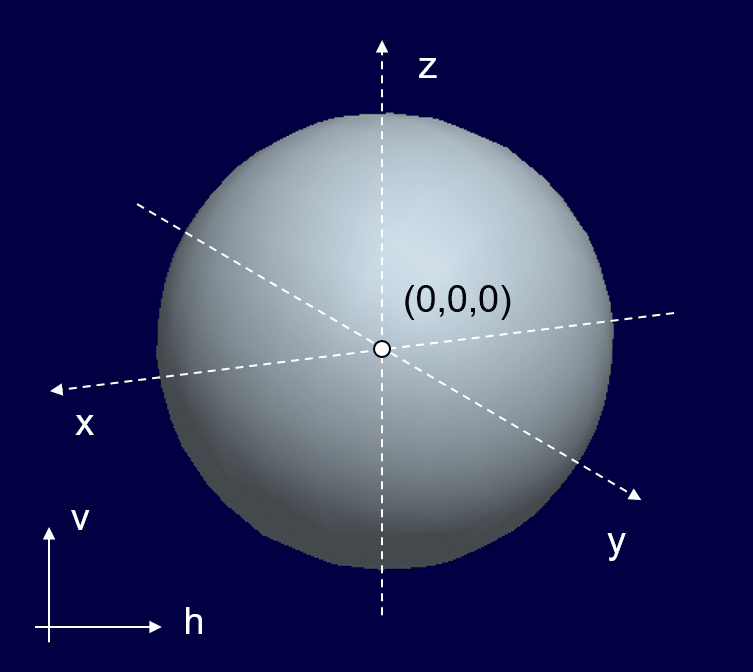
スクリーンの座標は、最終的にTableauのVizを作るときに必要な、縦と横の座標情報です。元の空間座標(x, y, z)と区別するために、「h」,「v」という新たな軸で考えます。あなたは今、三次元空間にいて、少し上から球を見ています。目の前にはスクリーンがあって、上図のように球が投影されています。

もう少しわかりやすくするために、球の上半分を切断しました。そして、z = 0 の高さからこの半球を見ているとします。赤矢印から見た時、x軸と球の交点にある黄色の点はどのように見えるでしょうか?「h」と「v」の原点は、もとの三次元空間の原点に重ねてあります。

スクリーン上ではこのように見えるはずです。目線は z = 0 ですので、黄色の点はh軸上(v = 0)にあります。この時、黄色の点がどのくらいに左に見えるか?を計算することが出来れば、投影図を描くことが出来ます。
座標軸の回転

先ほどは、x軸からθ度だけ右から見ていましたが、目線をx軸上に変えてみます。すると黄色の点は、スクリーン上でどのように見えるでしょうか?
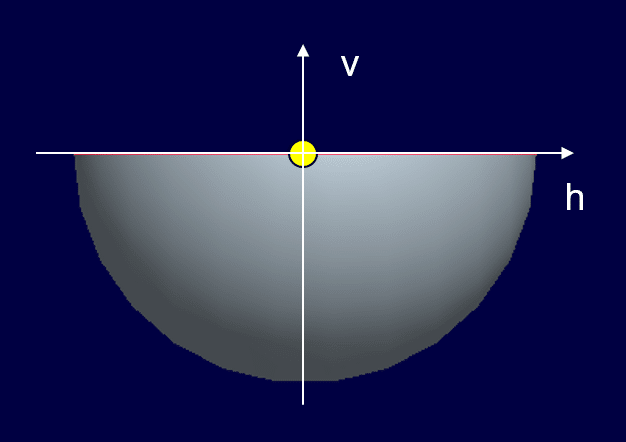
黄色の点は、真ん中(原点上)に重なって見えます。これは、比較的イメージしやすいはずです。「水平方向(z軸周り)に目線をθだけ動かすと黄色の点は原点に戻る」ということは、「最初の目線で左に見える距離は、軸をθだけ回転させた分」と捉えることが出来ます。これが私なりの変換2の解釈です。ここで、先に説明したベクトルの一次変換が役に立ちます。

変換2の中身(3行3列の行列式)については今回は触れません。この行列式で変換すれば、水平方向にθだけベクトルを回転できるおまじないだと思ってください。

ここまでくると、変換3が何をしているのかは概ね予想がつくはずです。スクリーンの位置を、垂直方向にφだけ回転させています。上から見れば見るほど、スクリーン上の黄色い点はv軸のマイナス方向に動いていきます。
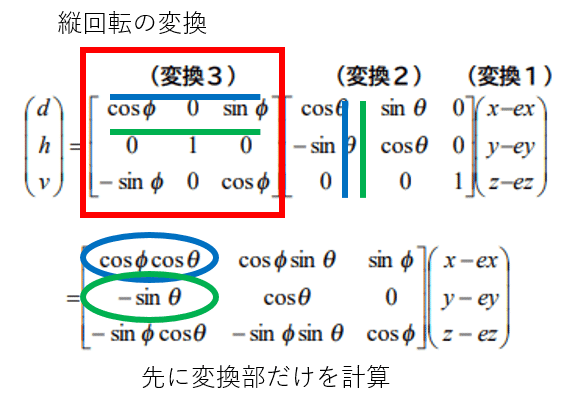
ここで、下の行列式に着目します。これは変換2と変換3を先に計算しています。それぞれの行と列をかけて足すという演算規則に従って考えれば、行列の成分は理解できるはずです。実際のTableauの計算フィールドではこの行列式を使います。
原点の移動
最後に、変換1について説明します。これは、途中で述べた「hとvの原点を、もとの三次元空間の原点に重ねる」という作業です。ex, ey, ezは自分がどこから見ているかの情報です。つまり、「ここにスクリーンを置いて、原点中心にVizを描く」と定義しています。
では実際に、Tableau上でVizを作ってみます。データはおなじみのサンプルスーパーストアを使います。はじめに、3つのパラメーターを使って、自分がどこから見るかを決めます。
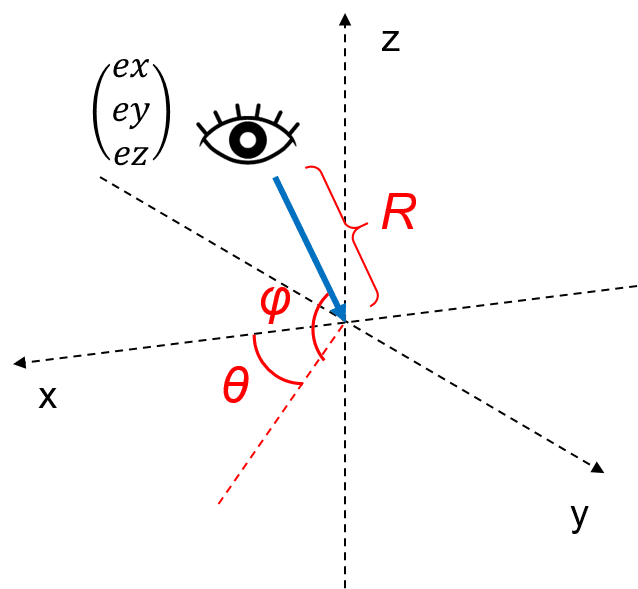
目線の位置座標 (ex, ey, ez) は以下の計算式で表すことが出来ます。これは三次元極座標といいますが、言い換えるならば地球の緯度(φ)と経度(θ)の情報から三次元の座標 (x, y, z) を計算しているようなものです。

投影図の座標計算
次に、俯瞰したい元のVizを作ります。オーダー日の月(1月~12月)を円に並べてみました。1周(360°)を12等分するので1つの要素の角度は30°です。二次元の極座標変換については過去のNoteで解説しています。xy平面に円を描きたいので、zは0としました。

ここからは、本Noteの集大成といえる計算フィールドを作ります。これを理解するために、ここまで長々と説明してきました。ステップとしては2つで、原点の移動とベクトルの一次変換です。

まずは、原点の移動をしますが、これはとても簡単な計算式です。すでに作成したx, y, zから、ex, ey, ezそれぞれを引いた計算フィールドを作成してください。
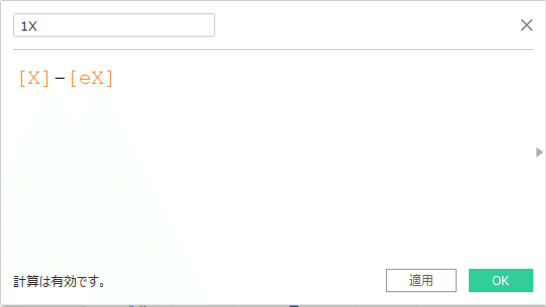
次に一次変換の部分です。もう一度、行列の積の演算規則をおさらいします。1行目と1列目をそれぞれかけて足したものが新たな1行目になるので、「d」の値は以下のような計算式になります。


パラメータの「Phi φ」と「Theta θ」は0~360の整数で与えているため、RADIANS関数を使って角度に変換しています。同様に、「h」と「v」も計算フィールドを作成してください。
得られた「h」と「v」がスクリーン上の新しい座標になりますが、ここではMAKEPOINT関数を使いました。理由は、マップデータに変換してマークレイヤーの機能を使うためです。複数のマークを重ねることで、自由度の高いVizを作ることが出来ます。

dの意味
「h」と「v」はスクリーン上の縦横の座標でしたが、計算結果には「d」も出てきます。この値は、もとの座標からスクリーンまでの距離に相当します。正確には、dは下図のベクトルとは向きが逆であり、基本的に負の値を取ります。距離として考えるならば、-dが正しい値です。
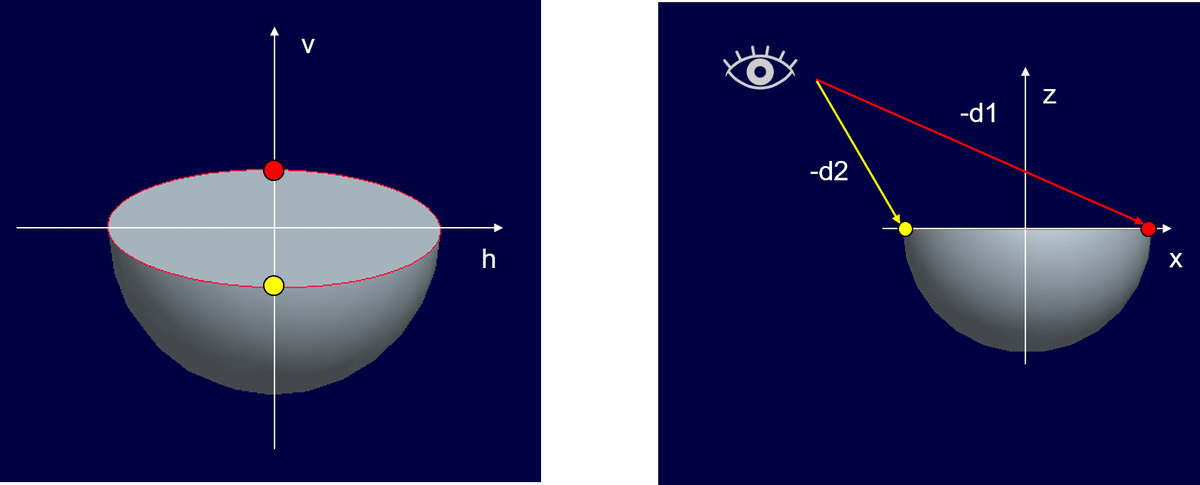
つまり、-dの計算フィールドをサイズに使うことで、遠近感を演出することが出来ます。遠くのものほど-dの値は大きいので、サイズを反転させるか、-dの逆数(1/-d)を取ってください。ただし、今回は距離を考えるために-dで説明しましたが、実際のVizではdをそのまま使えば、サイズを反転させる必要はありません。

ここから先は、個人の表現の自由です。Viz作成にあたり、以下のポイントに注意してください。
MAKEPOINTと、その粒度となるフィールド(今回はオーダー月)を詳細に入れる
dをサイズで使う場合は平均値にする(合計にしない)
[マップ]→[バックグラウンド レイヤー]からウォッシュアウトを100%にすることで背景色を消すことができる
zを応用した立体的なViz
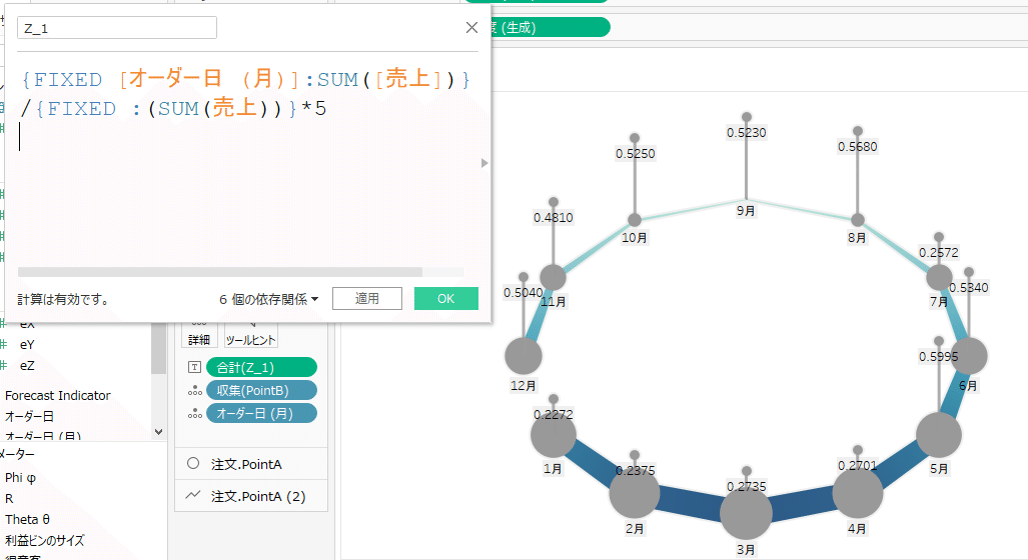
今回はx,y平面に円を描いただけなので、z = 0 に固定しましたが、何かしらのメジャーバリューを入れることで、立体的なVizを作ることが出来ます。その場合、必要な計算フィールドを複製し、新たに作成したMAKEPOINTをマークレイヤーとして追加して下さい。注意する点は、集計と非集計の混在です。メジャーバリューを非集計として扱いたい場合、私はVizLODに合わせたFIXED計算を使って先に計算しています。この時、売上の合計をそのまま使うと値が大きすぎるため、合計に対する割合に5をかけて、見た目の高さを調整しています。
さいごに
今回は、ベクトルと行列についてお話させて頂きましたが、私自身もすべてを理解しているわけではありません。ただ、今回のNoteを読んで、一人でも多くの方に「投影図を作ってみようかな」と思っていただけると嬉しいです。
最後に、今回使ったワークブックを載せておきますので、是非ダウンロードして理解を深めるための参考にして下さい。ここまでお付き合いいただき、ありがとうございました。
それでは、また。
