
ピンポン玉から放物線を求める
こんにちは。
今日はピンポン玉が跳ねる様子から放物線を描いてみます。
撮る
家にピンポン玉があったので使います。
iPhoneのスローモーション機能で跳ねる様子を撮影しました。
グラフにする
トラッキングさせる
この映像を3DCG制作ソフトウェアBlenderにインポートします。
Blenderには映像をインポートしてトラッキングできる機能があるので、そちらを使います。
このように特徴的な部分(今回はピンポン玉)を追従させることができます。

ちなみに、壁と床の境界付近でトラッカーが迷子になることがよくありました。

高さをグラフにする
次に、3D空間上の球体を追従させたトラッカーにくくりつけます。

まるで本物のピンポン玉みたいですね。
そうしたらこの球体の高さをキーフレームに保存します。

これをグラフにすると…

放物線の完成です!!!
放物線を観察
では、この放物線を数式を使って表してみましょう。
Desmosのグラフ機能を使います。

画像をインポートして、
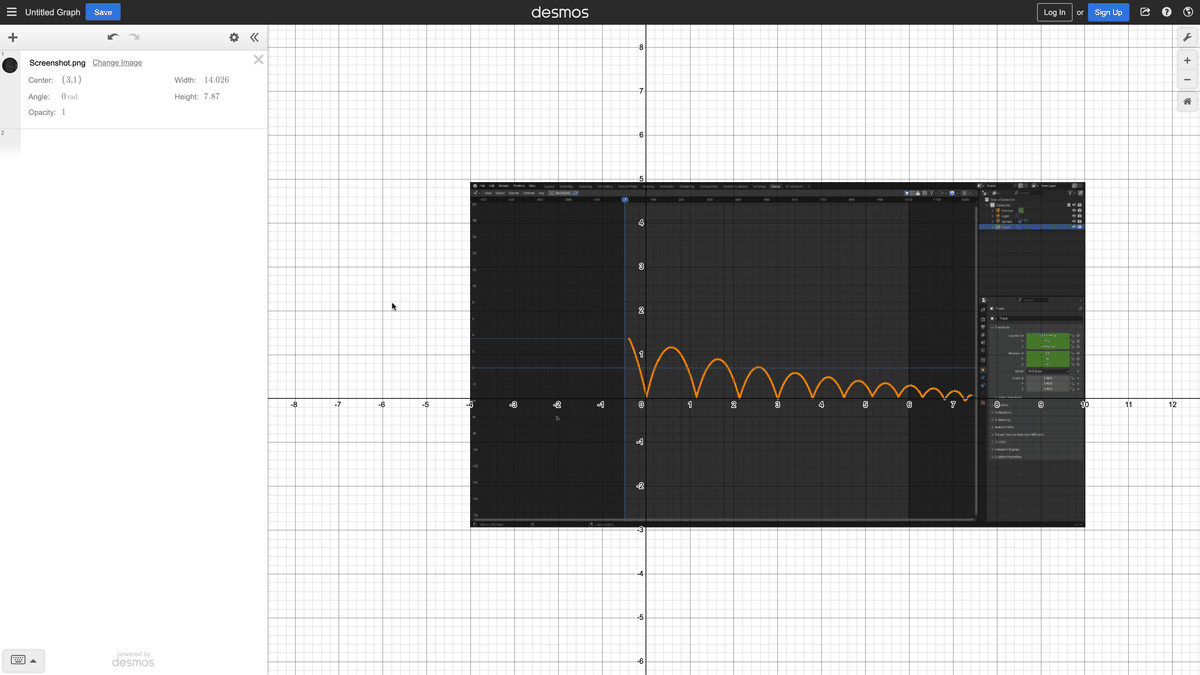
これに合う式を見つけます。

今回は$${y=-3.55x^{2}+4.0825x}$$でした。
ちなみにこのグラフには興味深い特徴があり、跳ね上がった部分のグラフはすべて合同(な図形を切り取ったもの)なんです。
動かしてみたほうがわかりやすいと思います。

このことをなにかの動画で見たような気がするのですが、覚えていません。わかり次第、ここに載せたいと思います。
反発係数を求めてみる
最後に、反発係数を求めて見ます。
詳しいことは知らないので省きますが、反発係数は$${\sqrt{\frac{跳ねた後の高さ}{跳ねる前の高さ}}}$$で求められるそうです。
$$
y=-3.55x^{2}+4.0825x
$$
の傾きが0の点が最大値なので
$$
\frac{dy}{dx}=-7.1x+4.0825=0
\\x=0.575
\\y=-3.55\cdot0.575^{2}+4.0825\cdot0.575=1.17371875
$$
これを跳ねる前の高さとします。
跳ねた後の高さは
$$
y=1.17371875-0.27=0.90371875
$$
とします。

なので、床とピンポン玉との反発係数は
$$
\sqrt{\frac{0.90371875}{1.17371875}}≈0.877
$$
です。
2物体間の反発係数は反発係数の乗算の平方根によって求まるため、床の反発係数を$${e_{1}}$$、ピンポン玉の反発係数を0.9としたとき、
$$
\sqrt{e_{1}\cdot0.9}=\sqrt{\frac{0.90371875}{1.17371875}}
$$
となるので
$$
e_{1}\cdot0.9=\frac{0.90371875}{1.17371875}
\\e_{1}=\frac{0.90371875}{1.17371875\cdot0.9}≈0.856
$$
とわかります。
おまけ
記事で使用したグラフへのリンクも載せます。ぜひ改造してみてください。
(おしまい)
※計算などに誤りがあれば教えて下さい。
いいなと思ったら応援しよう!

