
「0000」でMAKE10をしてみる
こんにちは。
MAKE10というパズルをご存知でしょうか?
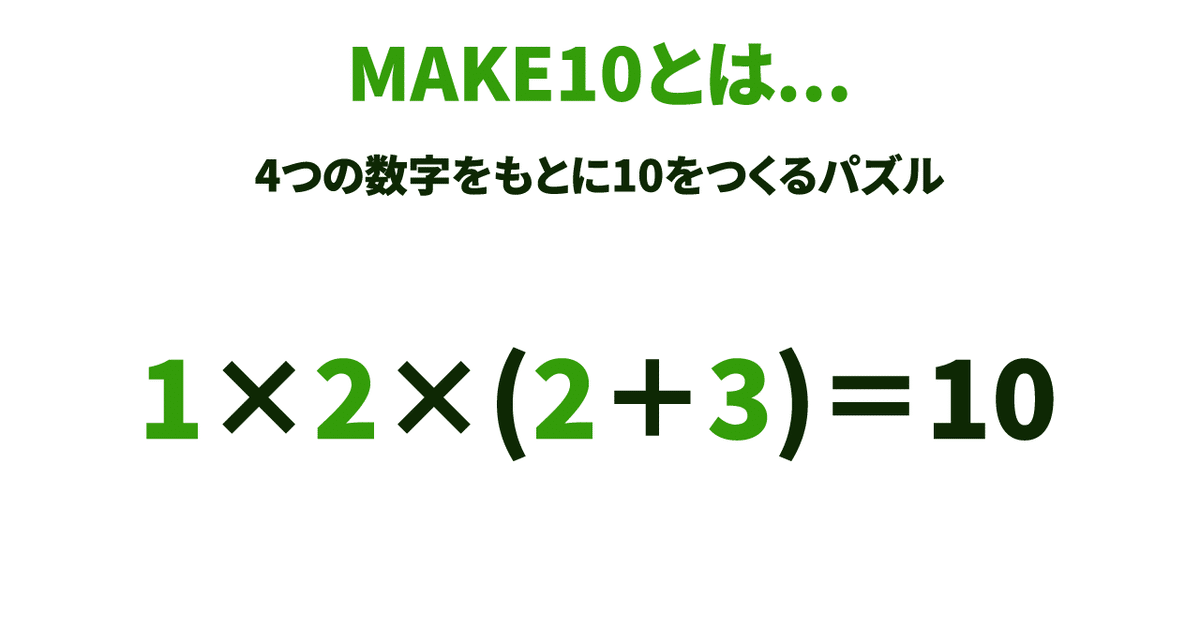
車のナンバープレートなどでやると楽しいのですが、一つ欠点があります。
それは、一部の数字ではできないということです。
例えば、0000だとどうあがいても10にはなりません…

…果たして本当でしょうか?
前提
MAKE10のルールを定めます。

いいですね。
1. (0!+0!)^3+0!+0!
まずは手始めに。
$$
(0!+0!)^{3}+0!+0!
$$
とかはどうでしょう。
計算してみると
$$
(0!+0!)^{3}+0!+0!
\\=(1+1)^{3}+1+1
\\=2^{3}+2
\\=8+2
\\=10
$$
とちゃんと10になります。
が、$${(0!+0!)^3}$$で3を使っていますね。ルールを追加します。

2. (0!-0!)÷(0!-0!)
$$
(0!-0!)\div(0!-0!)
$$
はどうでしょうか。
計算すると
$$
(0!-0!)\div(0!-0!)
\\=\frac{1-\frac{3}{3}}{1-\frac{3}{3}}
\\=\frac{1-0.00...1}{1-0.0...1}
\\=\frac{10}{1}
\\=10
$$
あるいは
$$
(0!-0!)\div(0!-0!)
\\=\frac{0}{0}
\\=10
$$
です。
$$
a = 10 \cdot b \iff \frac{a}{b} = 10
$$
なので
$$
a=0,b=0
$$
を代入して
$$
0 = 10 \cdot 0 \iff \frac{0}{0} = 10
$$
$$
0 = 0 \iff \frac{0}{0} = 10
$$
です。なので
$$
\frac{0}{0} = 10
$$
です。
…だめですか。

3. 0!+0!+0!-0!
$$
0!+0!+0!-0!
$$
を計算すると
$$
0!+0!+0!-0!
\\=2
\\=10_{\left(2\right)}
$$
ちゃんと$${10_{\left(2\right)}}$$になっていますね!!!
…ダメですか?

わかりました。
4. 0!÷.0!×0!×0!
$$
\frac{0!}{.0!}\times0!\times0!
$$
は計算すると
$$
\frac{0!}{.0!}\times0!\times0!
\\=\frac{1}{.1}\times1\times1
\\=\frac{1}{0.1}
\\=10
$$
になります。
…$${.0!}$$が引っかかりますね。

認めてくれませんでした。

5. !(dim { p(x) ∈ R[x] : deg(p) ≤ (0! + 0! + 0!) }) + 0!
いよいよ打つ手がなくなってきました。そこであまり一般的ではない計算まで視野にいれることとします。
Subfactorialという完全順列を求めるための方法があります。
これは$${!n}$$と表記され、$${!4=9}$$です。
$$
10=9+1=!4+0!
$$
なので4を0 3つ(=3)で表せば良いです。
果たしてそんな方法はあるのでしょうか。

ありました。
どうしてこうなるのかしっかりとは理解できませんが、0 3つで4を表現できていますね。
1次方程式のグラフは2次元上で表されるように、3次方程式が何次元上で表されるのかを求める式…かもしれない
なので!4+0!にこれを代入して

が答えですね。
ややこしい。
まとめ
強引にやるなら
$$
\frac{0!}{.0!}\times0!\times0!
$$
複雑でもいいなら

が答えです。
※計算に誤りがあれがおしらせください。
(おしまい)

いいなと思ったら応援しよう!

