三角関数とはpart3 タンジェント

※part4が投稿されるとは限りません
※誤植、間違いがあれば教えてください

3.1.三角比としてのタンジェント

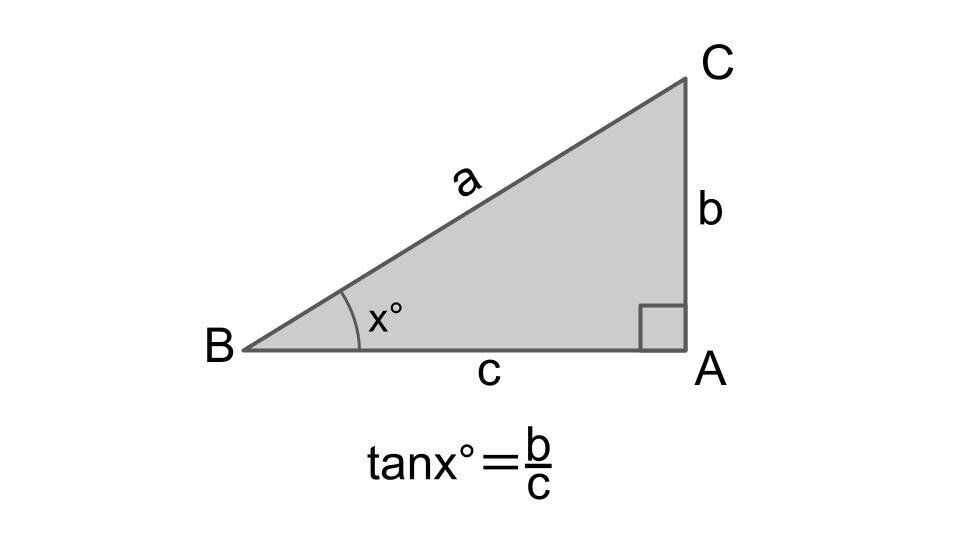
定義１
∠A=90°であるような直角三角形ABCに対し、∠B=x°、AB=c, AC=bとすると、tanx°=b/cと定義される。

例１（二等辺直角三角形におけるtanの値）
∠A=90°とする二等辺直角三角形ABCについて、∠B=45°であり、AB=ACとなるからtan45°=1だとわかる。

問１
part1の例２を参考にして、tan30°、tan60°の値を求めよ。
※part1はこちら

命題１
tanx°=(sinx°)/(cosx°)が成り立つ。

証明
∠A=90°, ∠B=x°, BC=1であるような直角三角形ABCを考えると、part1の命題１からAB=cosx°、AC=sinx°となるため、tanx°=AC/AB=(sinx°)/(cosx°) ▢

3.2.三角関数としてのタンジェント

定義２
x≠90+180n（nは任意の整数）とする。このとき、tanx°=(sinx°)/(cosx°)と定義する。ただしsinx°, cosx°はいずれも三角関数としての定義（つまりpart2での定義）とする。

※part2の記事はこちら

Rem
定義２の出だしでxの範囲を「x≠90+180n（nは任意の整数）」に制限した。これはx=90+180nにおいてcosx°=0となり、tanx°をうまく定義することができない。そのためtanx°は、値が定義されない点xが無数に存在する、すこし変わった関数なのである。

例２（tan135°、tan225°、tan315°の値）
x°=135°, 225°, 315°のときのsinx°とcosx°の値はそれぞれ
sin135°=1/√2、cos135°=－1/√2
sin225°=－1/√2、cos225°=－1/√2
sin315°=－1/√2、cos315°=1/√2
以上から、tan135°=－1、tan225°=1、tan315°=－1

問２
tan150°、tan300°の値をそれぞれ求めよ。

3.3.タンジェントを含む基本的な公式

命題１
x≠90+180n（nは任意の整数）のとき、1+(tanx°)²=1/(cosx°)²が成り立つ

証明
part2の定義１から点(cosx°,sinx°)は単位円x²+y²=1上にあるから、
(cosx°)²+(sinx°)²=1が成り立つことがわかる。よってx≠90+180n（nは任意の整数）よりcosx°≠0なので、両辺を(cosx°)²で割ることにより命題１の等式を得る。▢

以上