
■「ヒエラルキー分業」から対等共食へ転換を急げ!“リアル循環の変異の閾値”の調整弁たる不均衡動学(社会的共通資本のヒュレー)の基本ツール、数学の「本来性と言語性」の活用は「リアリズム倫理」の良循環をもたらす!(2/4)
2 AIディープラーニング時代の数学の役割/宇沢理論(不均衡動学)を支える数学の考え方
(数学は不均衡動学、つまり"社会的共通資本『変異の閾値』調整の必須ツール)
『宇沢弘文の数学』(青土社)の著者・小島寛之氏(宇沢弘文と同じく東京大学理学部数学科・卒業の経済学者)は、「数学は、人間社会にとって最も基本と見るべき社会的共通資本の要である」との主旨を述べられている。また、このことを宇沢弘文が「インネイト」(innnate)と呼んでいたことを紹介している。Innateは、「人間には、先天的な生まれつきの能力(本来性/そもそもはハイデガーの用語)として、言語能力とともに数認識・図形認識・論理操作の能力が備わっていることを意味する。
ところで、『無限のパラドクス』(講談社ブルーバックス)の著者・足立恒雄氏によれば、現代における「無限」論では、無限を数学的無限(空間)、物理的無限(空間)、哲学的無限(空間)の三つに分け、これらは異質なものと考えるのが一般的である(数理論理学(記号論理学)は曖昧な点があり、これらの区別をつけ難いが)。
また、現代の数学は非常に厳密で誤りのない学問だが、物理学などの科学(理論と技術)は絶対的に正しいとまでは主張できず、絶えず演繹的な論証、又は実証によって修正されたり、場合によっては否定されたりすることもある得る。そのため、『宇沢弘文の数学』(青土社)の著者・小島寛之氏が指摘するとおり、まず数学は、そもそも「その本来性」によって社会的共通資本の活用にとり特に重要と見るべきツールである。
しかし、それと同時に数学には「その本来性のもう一つの重要な特性である言語性」故に、逆に人間を「カテゴライズ(分類・区別・差別)」するためのツールとして利用されるリスクも抱えている。特に、そのような傾向はデータサイエンス、AI深層機械学習(ディープラーニング)、統計などで利用される場合にそのリスクが大きくなる。また、小島寛之氏はシナリング(signaling/ゲーム理論の用語)と呼ばれる「テスター」(TESTER/数学の能力でヒトを一面的に評価する選抜主義)のリスクが数学の「技術性と言語性」の中に潜むことを指摘している。
因みに、経済動学論など数理経済学の場面で活用される「関数」について、ごく大まかに概観しておくと、以下のとおりとなる。関数は、まず<例えば「外延性の公理(全く同じ要素からなる2つの集合は等しい/https://unaguna.jp/article/archives/11)=集合はそれに属する全ての数学的対象を指定することで特徴づけられる」などの諸「公理」を前提としている。
そのうえで、関数は「数の集合で値をとる写像」、つまり世に存在する限りの凡ゆる集合を“フレーゲ流の1対1対応(直感的に集合と集合を対応させる集合算)”(“ペアノ流の指折りで数えることを基本とする数え主義”の対概念)で類別して生ずる新たな集合(属性)の抽象化(分析哲学で言う個々のトークンに対する、新たなタイプの創造に相当する?)の写像である、と定義される。
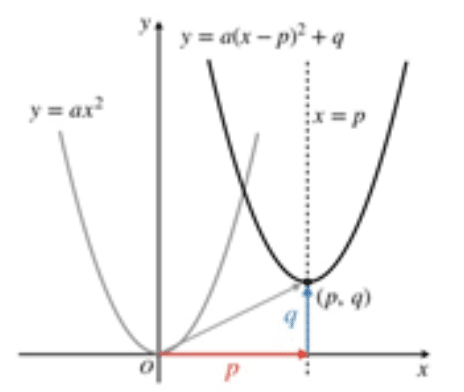
そして、その単純な事例は一次関数(y=ax+b)、二次関数(y=ax2+bx+c)などである>ということになる。なお、集合の公理系(公理体系)には多数のものがあるうえ、更に微分・積分らのファクターが加わることで非常に複雑な多次元関数の形となる(https://www.komazawa-u.ac.jp/~takai/kougi/AxiomaticSetTheory.pdf)。
<補足>
フレーゲ流の集合算(例えば、3+4=7)の方は、より自然数の本質を直感させるため数学の“本来性”および“言語性”と親和力が大きい。一方、“ペアノ流の数え主義”は、やや数学の“技術性”と深く関わる傾向があるため数学的帰納法を介しアルゴリズムやプログラム言語の基礎となっており、現代のコンピューター・テクノロジーを支えている(関連参照 →後述の『3‐ 宇沢理論(不均衡動学)と古澤理論(不均衡進化)が共有する『変異の閾値』の問題/数学の本質と社会的共通資本が共有する五つの特性)』)。なお、数学的帰納法は一般的な意味での帰納法ではなく、純粋に自然数の構造に依存した演繹論理の一種(つまりその意味で直感主義的、演繹論的である)で、例えばドミノ理論の如く次々と命題の正しさが"伝播"され、任意の自然数に対し命題が証明される過程が"帰納"の様に見えるため、この名称がつけられた/具体的な説明はコチラ → https://mathtrain.jp/kinouhou)
(関数の写像イメージの事例)
一次関数(ユークリッド平面空間)のイメージ(事例)ウイキより
二次関数(ユークリッド平面空間)のイメージ(事例)
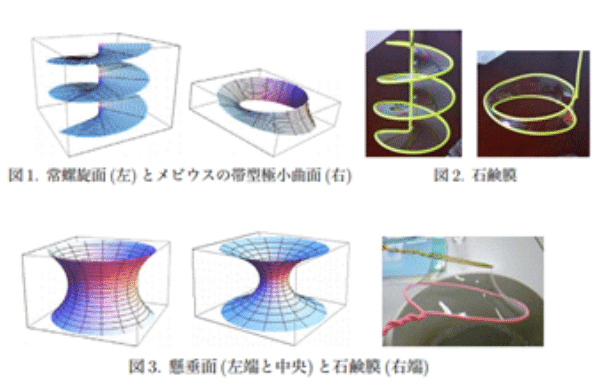
二次関数/極小曲面(石鹸膜の数学的抽象化):三次元空間で観察される二次元イメージ(特殊な事例/石鹸幕)
https://www.math.kyushu-u.ac.jp/Ext-Course/Open-Lect/zi_liao_files/koiso2011.pdf
・・・自然界で観察(実験を含む)される物理法則の多くは,「なんらかのエネルギーが最小または極小となる状態」として表現することができる。これを「変分原理」と呼び、このような最小値や極小値に関する問題を「変分問題」と呼ぶ。変分問題は、数学の理論としても、また自然現象を記述し解明する方法としても重要であり、物理学、工学その他さまざまな分野へも応用されている。
二次元平面に表示した三次元関数のイメージ(写像の事例)
https://www.ipc.tohoku-gakuin.ac.jp/neichi/javaAnalysisTools/manuals/helpFunction3DDraw.html
https://jp.mathworks.com/help/matlab/ref/fimplicit3.html
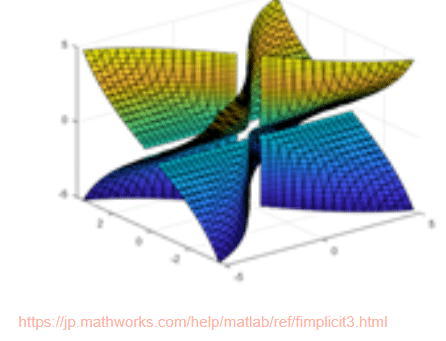
(補足)トポロジー(位相幾何学)世界の拡がり(n次元超球体、結び目理論、クラインの壺など)
・・・極小曲面は、古典的な三次元ユークリッド空間 R3 内の立体の境界として得られる曲面である。例えば、球体の境界としての球面はそのようなものの例になっている。ユークリッド平面(二次元平面)の円周が三次元球体の表面(三次元球面)であるのと同じことで、三次元球面は四次元球体の表面、四次元球面は五次元球体の表面…ということになり、「n次元超球体の表面=(n-1)次元表面」の関係となる。
・・・このような入子構造の関係は、立方体・錐体・直方体・正多面体など無数に存在することになるが、各n次元多面体と二次元平面との関係、および半径rの場合の各表面積ないしは体積などは数学的に表現できる。また、このことから空間そのものも多次元の入子構造(あるいは結び目による結びつきの構造)、つまり結び目理論で無限に拡がっていることが推測される。
[関連資料3/結び目理論の科学への応用-プリオン分子モデルとこころのモデルを中心として-河内明夫・名誉教授(大阪市立大学大学院理学研究科/<注>著名な結び目理論の研究家)]:数学の結び目理論とは, 結び目, 絡み目, あるいは空間グラフの、モノとしては同じだが、 配置が異なる場合のその差異を数学を使って研究する学問であるといえる。https://mathsoc.jp/publication/tushin/1404/1404kawauchi.pdf
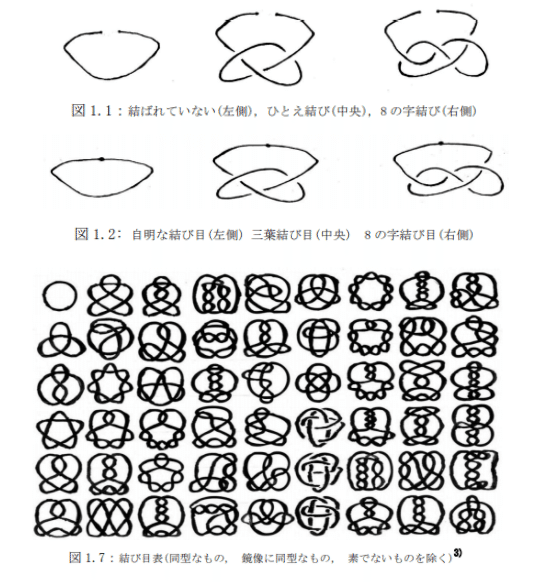
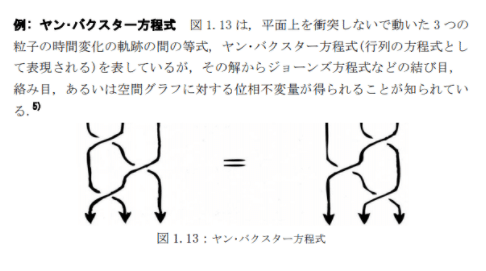
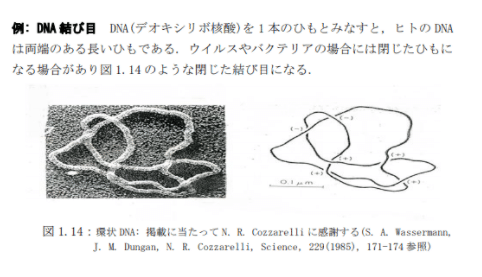

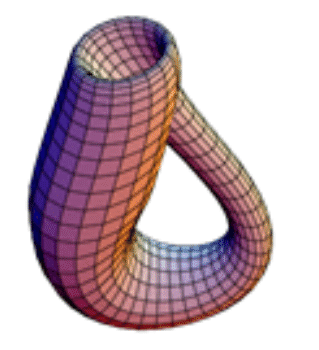
・・・ところで、『クラインの壷』など特異点や自己交叉を持つことなしに三次元ユークリッド空間に埋め込み不可能な曲面というものも存在する。曲面が「二次元」であるということは、それが二次元の座標系を入れた「座標付きのきれはし」の貼り合せになっている(リーマン多様体(いわば“変異の閾値https://www.chitose-bio.com/furusawa_column/column28.html”的な空間?(@toxandoria))
但し、地球の表面にいる我われの目が平面しか意識できないのと同様に、その超ミクロの二次元の抽象化である極小曲面にR3側から接して立つことができる者の目には平面しか見えない筈だ。
しかも、仮にその極小曲面の薄膜層(数学理論上は抽象化された実体のないものの筈だが、例えば石鹸膜(シャボン玉などの)の実在する極小面の実体は超ミクロと雖もリアルな一定の厚さを持つ実在(三次元の存在)の筈だ!)の内部に入ることができた者がいるとしたとき、その者の目はどの様な外界の光景を見るのであろうか?それは地球上と同じくユークリッド平面の地平なのだろうか?残念ながら、このことに触れる文献は今のところ見当たらない!(苦w)
上に掲げた『クラインの壺』(画像ははウイキより)をユークリッド空間に埋め込むには4次元、曲率0とすると5次元が必要である。だから、3次元空間には通常の方法では埋め込み不可能だが、射影して強引に埋め込むと、自己交差する3次元空間内の曲面になる。その形を壺になぞらえたものが当イメージである
https://ja.wikipedia.org/wiki/%E3%82%AF%E3%83%A9%E3%82%A4%E3%83%B3%E3%81%AE%E5%A3%BA)。
・・・また、四次元空間以上の多次元空間はイメージできないとされてきたが、極小曲面の数学的な研究が進むにつれて、共連続構造(Ex. ABブロック共重合体の共連続構造を与える三重周期極小曲面/結び目による空間の連続が可能?)等の研究によって、例えばブラックホールなど未知の空間の多次元構造が推測されるようになってきている。
https://www.jst.go.jp/crest/math/ja/caravan/20141129_Mito/1-Koiso.pdf


<参考>複雑経済の見方、先人(高橋亀吉)に学ぶ2021.2.13日本経済新聞
https://twitter.com/tadanoossan2/status/1361938788348358656
(注)高橋亀吉(1891 – 1977/経済評論家・経済史研究者、石橋湛山と並ぶ日本の民間エコノミストの草分け的存在。元・東洋経済新報社編集長など歴任。https://kotobank.jp/word/%E9%AB%98%E6%A9%8B%E4%BA%80%E5%90%89-92705
◆「高橋亀吉の眼差し=ヒト(日常の多様性でこそ生きられる)のための経済、およびロイ・ハロッド(シュンペーターに先行する経済動学化の祖)&ケインズ重視」との理解は慧眼!
・・・例えば、ミルトン.フリードマンの市場原理主義(非ユークリッド重力理論の援用)も、or 流行りのAIディープラーニングと雖も、その実態は殆どが「高次元数学空間」の写像であり、それは「リアル自然&ヒトの日常」とは異次元!又、人間の思考と断絶するディープラーニングが人間社会&自然の多様性と対極の閉鎖性(分断・排他・差別別主義)の罠に落ち易い性向を持つ危険性のあることがAI研究者自身により自覚されつつある(Ex.↓★)。
★アルゴリズムデータサイエンス機械学習/ディープラーニングの限界、POSTD https://postd.cc/the-limitations-of-deep-learning/
★深層計算(多層計算)“ブラックボックス”問題(深層計算ではベイズ統計の帰納論理(多層機械処理の不分明さ」だけでなく、そもそも所定の母集団の概念がなく、得られたデータから確率を何回も更新する)が思想ベースとなっていることも当問題の一因!)に関するエトセトラ、https://toxandoria.hatenablog.com/entry/2019/09/02/125003
・・・故に、同じ経済動学の手法であるとしても、例えば宇沢弘文「不均衡動学」の如く、「経済成長=リーマン幾何学的な多次元空間における巡航速度(必須のベクトル成分)と理解しつつも、同時に、特に日本政府は、格差の是正&抑制への真剣な努力で、それが実際に「日常でリアルに生きるヒト」のため役立つよう、つまり、「Fiduciary/リアリズム倫理」(ベースは社会的共通資本)を最重視することで、たとえば非ユークリッド(リーマン)曲面における接成分0の“曲線”あるいは曲面の測地的曲率ら、3次元空間で生活する一般の人々には中々実感し難い「抽象論理の成果」(or AI機械高度生産性)を、いわば我われが日常的に理解しやすい「“ユークリッド直線”(測地線)等に相当するリアル分配所得(生命論的、つまりエネルギー通貨的な経済価値)」へ読み替え、翻訳できるようにする具体策(ベーシックインカムはそのための基本である!)へ取り組むことで、経済学あるいはAIディープラーニング(膨大な数の高次元関数が連鎖する深層学習による特徴点の算出)など先端科学技術の成果を普通一般の人々が日々の幸福のため本格的に、かつ安心して日々に利用できるような方向へ大急ぎで社会的選択(政治経済)の軌道修正を図るべきである。 → 複雑経済の見方、先人(高橋亀吉)に学ぶ2.13日本経済新聞https://nikkei.com/article/DGKKZO69080710S1A210C2EN2000/
(宇沢弘文『社会的共通資本』について)
<注>(1)「不均衡動学の内容」および(2)「社会的共通資本と不均衡動学の関係」については、下記◆を参照乞う。
◆宇沢弘文「経済学の考え方」-岩波新書-(1)
◆大塚信一「宇沢弘文のメッセージ」-集英社新書-(1)
◆「環境」を分析できる理論に挑み続けた経済学者の遺言=佐々木実 2020年2月24エコノミスト https://weekly-economist.mainichi.jp/articles/20200303/se1/00m/020/044000c (1)
◆市場原理主義(ミルトン・フリードマンら)の天敵!宇沢論文「不均衡動学」の理論 https://toxandoria.hatenadiary.jp/entry/2021/02/02/022035 (1)

◆宇沢弘文、傑作論文全ファイル-東洋経済新報社-(2)
◆宇沢弘文「経済動学の理論」:1986 -東大出版会-(2)
◆宇沢弘文著作習5「経済動学の理論」-岩波書店-(2)
・・・下記★より、部分転載/なお、『社会的共通資本』と一体、いわばそれと表裏の関係にあると見るべき宇沢弘文『不均衡動学』(動学経済理論)の委細については、同じく下記記事★を参照乞う。・・・
★日常を凝視するスウェーデンモデルへの宇沢弘文の貢献とFiduciary(リアリズム倫理)に無知なスガ「Kook権力」の玩具と化し不幸のどん底に嵌る日本国民!https://toxandoria.hatenadiary.jp/entry/2021/02/02/022035
宇沢弘文は、次のように説明している。まず概念的には、以下の三つに纏めることができるが、数学と言語は、「(3) 制度資本 : 教育,医療,金融,司法,文化」のカテゴリーに入る。
ゆたかな経済生活を営み、すぐれた文化を展開し、人間的に魅力ある社会を持続的、安定的に維持することを可能にするような自然環境や社会的装置.
社会全体にとっての共通の財産であり、それぞれの社会的共通資本にかかわる職業的専門化集団により、専門的知見と職業的倫理観にもとづき管理、運営される.
一人一人の人間的尊厳を守り,魂の自立を保ち,市民的自由を最大限に確保できるような社会を志向し,真の意味におけるリベラリズムの理念を具現化する.
具体的には、以下のように類型化できる。
(1) 自然環境 : 山,森林,川,湖沼,湿地帯,海洋,水,土壌,大気
(2) 社会的インフラストラクチャー : 道路,橋,鉄道,上・下水道,電力・ガス
(3) 制度資本 : 教育,医療,金融,司法,文化
・ この分類は必ずしも網羅的ではなく排他的でもないあくまで社会的共通資本の意味を明確にするための類型化である
・ それぞれの社会的共通資本にかかわる職業的専門化集団により、専門的知見と職業的倫理観(フィデューシャリー(fiduciary))にもとづき管理、運営される。
・・・
その他の記事はコチラです! ↓
(1/4)https://note.com/toxandoria2/n/n28426341adf1
(3/4)https://note.com/toxandoria2/n/nfc58c11fea2d
(4/4)https://note.com/toxandoria2/n/nb90cf07acd1b
・・・全体の記事は下記◆にあります。
◆「ヒエラルキー分業」「ヒエラルキー分業」から対等共食へ転換を急げ!“リアル循環の変異の閾値”の調整弁たる不均衡動学(社会的共通資本のヒュレー)の基本ツール、数学の「本来性と言語性」の活用は「リアリズム倫理」の良循環をもたらす! https://toxandoria.hatenadiary.jp/entry/2021/03/08/233246
◆【別ヴァージョン】「ヒエラルキー分業」から対等共食へ転換を急げ!“リアル循環の変異の閾値”の調整弁たる不均衡動学(社会的共通資本のヒュレー)の基本ツール、数学の「本来性と言語性」の活用は「リアリズム倫理」の良循環をもたらす!https://toxandoria.hatenablog.com/entry/2021/03/08/180245
