
【DNCL/プログラミング】共通テスト情報Ⅰ 試作問題 第3問解説【解法テクニック】 (大学入試センター 2022/11/9発表)
はじめに
情報関係基礎にも、DNCL(大学入学共通テスト用の擬似プログラミング言語)が出題されていましたが、それに比べてかなり解きやすくなった(問題本文にヒントが沢山ある)という印象です。
ただ、15分で解答するにはそれなりの読解力+テクニックが必要と思うので動画内でも説明しています。
書籍出版します!
テクニック解説動画(第3問)
問題のダウンロード
問題の出典:大学入試センター
動画制作
文字おこし
大学入学共通テスト 情報Ⅰ 試作問題 今回は第3問 の解説を行っています。
問1から問3までありますが、問1で詳しく説明したアルゴリズムの内容が問2、問3のDNCL擬似言語のプログラミング問題に紐づいていきます。
逆に、問1で意味を理解しないと、問2と3を芋づる式に落としてしまう可能性があります。

問題の本文は読んでいることを前提に、空欄解答に必要な思考プロセスを中心に説明していきます。

問1から見ていきます。
テーマは、「客が支払う枚数と釣り銭を受け取る枚数の合計を最小にする払い方」になります。
今回は46円の品物を買ったときの例で詳しく説明があります。この例の内容を理解すればこの後の問題が容易に解けます。
46円のおつりの出ない支払いだけで考えると、10円玉4枚,5円玉1枚,1円玉1枚という6枚での払い方が最小の枚数となります。
支払に対してのおつりの受け取りも考慮すると、50円玉1枚と1円玉1枚 合計51円を支払って、釣り銭5円を1枚を受け取る方法だと、支払いに2枚,釣り銭に1枚で,合計3枚の硬貨で済みます。
このような、「最小交換硬貨枚数」の計算を考える問題になります。
――

そして重要なのが、枚数関数に関する説明になります。
引数として「金額」が与えられ,ちょうどその金額となる硬貨の組合せの中で,枚数が最小となる硬貨枚数が戻り値となる関数。とあります。
8円の最小硬貨枚数は、5 円玉が1 枚と1 円玉が3 枚で合計4枚になるのは先ほど説明した通りです。
この関数を使えば、丸カッコ内が金額を表していて、金額(8)とすると、8円の最小硬貨枚数である、4という数字が返却される関数になります。
空欄アは 枚数関数の引数に46を渡した時の戻り値の数が問われています。
これは、初めに46円の例で「10円玉4枚,5円玉1枚,1円玉1枚という6枚で払い方が最小の枚数」と説明した通りで、戻り値は6が返却されます。よって空欄アは6になります。

空欄イは46 円支払うのに,51 円払って5 円の釣り銭を受け取る払い方をした場合,客と店の
間で交換される硬貨枚数の合計について枚数関数を使うとどうなるかについて問われています。
先程の例で説明したように
51円の支払いの時点で2枚、5円のおつりで1枚の合計なので
これを関数で表すと、枚数(51)で2が返却され、枚数(5)で1が返却されるのでこれを足し合わせると3になります。
つまり空欄イの答えは0番になります。

次に空欄ウ、エの部分を確認していきましょう
商品の価格をx円、釣銭をy円とした場合の、引数を変数で答えさせる問題です。
変数になると苦手意識を持つ人も多いと思いますが、実際に値を当てはめて考えると容易に解けることが多いです。
先程の問題に戻って考えると
引数の始めの51は、商品価格の46円と釣銭の5円を足した金額です。
そして、後の5は釣銭の5円です。
商品の価格をx円、釣銭をy円と置き換えると
始めの関数の引数は商品価格+釣銭なので、x+y
後ろの関数の引数は釣銭のyになります。
足し算で順不同の答えでもよいので、空欄ウエは2番と1番になります。

次の問2では、問1で扱った関数「枚数(金額)」の中身を考えていきます。
また,金額に対して,ある額の硬貨が何枚まで使えて,残金がいくらになるかを計算するには,整数値の商を求める演算『÷』とその余りを求める演算『%』が使えるでしょう
という文言の後に、また46円のパターンで空欄オ、カを答える問題です。
計算式を考える前に46円に対して、10円玉が何枚使えるかは4枚ということが分かります。
この4を求めるのは、整数値の商を求める演算「÷」になります。
具体的には46÷10 で4が求められるので、空欄オは2番となります。
そして、余りの6を求めるのは、演算『%』になります。
具体的には46%10 で6が求められるので、空欄カは③番となります。
――

次の空欄キからコは、いよいよプログラムの穴埋め問題になります。
プログラムの問題を解くコツは
・変数の文字列だけで考えるとイメージできない場合があるので、必要に応じて実際に値をあてはめてみること
・本文の説明とプログラムが紐づいていることが多いので、このプログラム内の処理が本文で詳しく説明されていないか突き合わせること になります。
では、実際に上から本文と突き合わせ変数の意味を確認しながら処理を追っていきます。

1行目の変数Koukaは配列を表します。DNCLの表記ルールで、変数名の一文字目が大文字なのは配列を意味するので覚えておきましょう。
配列Koukaに硬貨の額を低い順に設定していて、添字は0から始まるとあります。
仮に2番目の5の値が欲しい場合は、Kouka[1]で取得します。
2行目の変数kingakuは、100円以下の目標金額を表し 最小枚数を求めたい金額になります。初期値は46が設定されています。
3行目の変数maisuは、支払いに使う硬貨の枚数の合計が入り、初期値は0です。
変数nokoriは、残りいくら支払えばよいか,という残金が入り、
初期値は変数kingakuの値で今回は46が格納されます。
4行目は繰り返し条件になります。
iを とあるので、変数iが何に使われているかを確認する必要があります。
しかし、7行目までの中にiが見当たりません。
そこで、空欄ケ、コの解答分を見ると、Kouka配列の添字指定に変数iが使われていることがわかります。
この繰り返し文に関する本文をもう一度確認すると、「高額の硬貨から何枚まで使えるかを計算する方針で,(4)~(6)行目のような繰返し文にした」とあります。
つまり、Kouka配列の一番最後の100の値から取得する必要があります。
Kouka配列の100の位置の添字は4で、1の位置の添字は0なので、「4から0まで1ずつ減らし」ながらループする必要があります。つまり空欄キは1番があてはまります。

次の空欄ク、ケについて見ていきます。
本文中に「変数maisuに支払いに使う硬貨の枚数の合計が計算され」とあります。。
つまりこの処理は、支払いに使う硬貨の枚数の合計する処理と考えられます。
前の問題で46円の時で10円玉で支払う枚数は 46 ÷ 10だったので、
残金である変数nokoriの値をKouka配列の添字iの要素で支払う枚数は、「nokori ÷ Kouka[i]」枚となるので、空欄ケは⓪番になります。
それに、今までの枚数を保持している、変数maisuの値を加えればよいので、空欄クは ①のmaisu になります。
ここは、実際の値を当てはめないと分かりずらいと思うので、あとで実際にシミュレーションしていきます。
――――――――――

空欄コについて、本文を見ると「変数nokoriに残りいくら支払えばよいか,という残金が計算されるとあります。」
先程の問題で、46円を10円玉で支払ったときの残金は今の残金%支払硬貨の
46 % 10で表せたので、これを今回の変数に置き換えると
① のnokori % Kouka[i]となります。

では1ループ目から実際に値を当てはめてシミュレーションしていきます。
5行目について
i=4なので、Kouka[4]は100になります。
46÷100の商は0 今のmaisuも0なので足すと0のままです。
6行目について
46%100 の余りは46になりますので、nokoriは46のままとなります。

2ループ目に入ります。
5行目について
i=3なので、Kouka[3]は50になります。
46÷50の商は0 今のmaisuも0なので足すと0のままです。
6行目について
46%50 の余りは46になりますので、nokoriは46のままとなります。
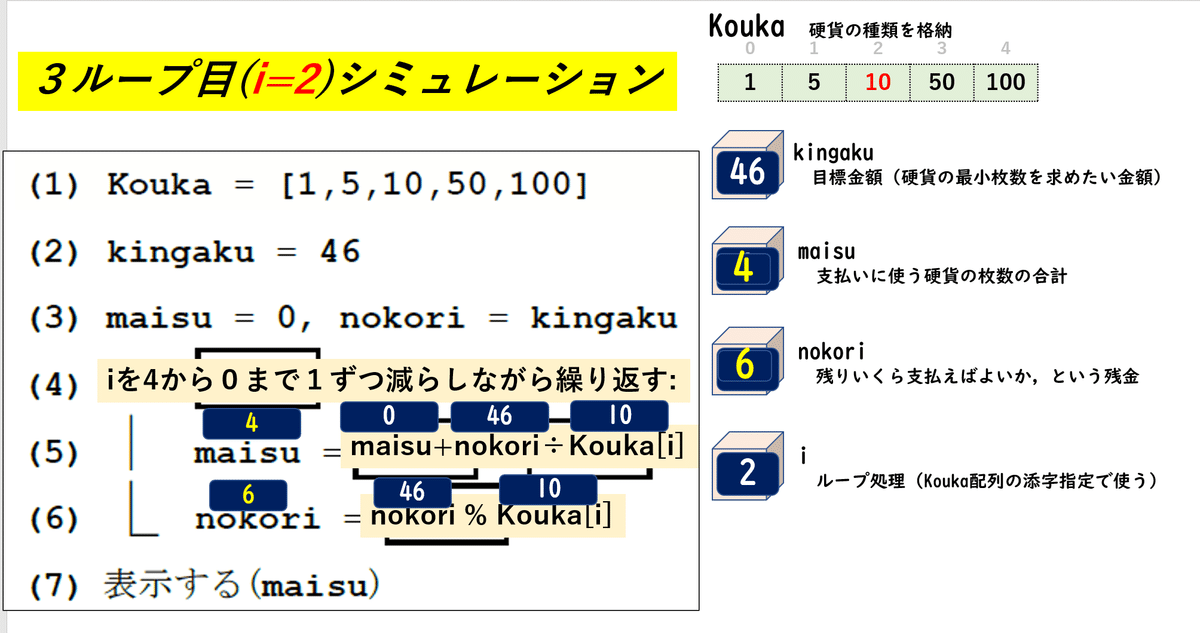
3ループ目に入ります。
5行目について
i=2なので、Kouka[2]は10になります。
46÷10の商は4 今のmaisuは0なので足すとmaisuは4となります。
6行目について
46%10 の余りは6になりますので、nokoriは6となります。

4ループ目に入ります。
5行目について
i=1なので、Kouka[1]は5になります。
6÷5の商は1 今のmaisuは4なので足すとmaisuは5となります。
6行目について
6%5 の余りは1になりますので、nokoriは1となります。

5ループ目に入ります。
5行目について
i=0なので、Kouka[0]は1になります。
1÷1の商は1 今のmaisuは5なので足すとmaisuは6となります。
6行目について
1%1 の余りは0になりますので、nokoriは0となります。
ループを抜けてmaisu変数の値の6が表示されます。
このように実際に値を当てはめてシミュレーションすることで、
問題を解く力が付いていきます。

問3は、問2で作成した最小枚数を計算するプログラムを呼び出していきます。
この問題は、問題本文とプログラムを突き合わせることで解答できるものになります。

まずは、空欄サ、シの繰り返し条件について見ていきます。
99という数字がヒントになり、99というキーワードで本文を見ると
「釣り銭無しの場合も含め、99円までのすべての釣銭に対し」とあります。
「釣り銭無し」は「0円」のことなので、0円から99円までの繰り返し処理を行っていると考えられます。釣銭は変数tsuriが対応しているので。
空欄サは、③のtsuri 空欄シは、0番の0となります。

次の空欄ス、セは 支払金額とおつりの合わせて硬貨の枚数を算出する処理になります。
問1の空欄ウ、エの処理が対応していて、必要な枚数は
枚数(商品価格+釣銭)+枚数(釣銭)で求められます。
商品金額+釣銭は、今回は支払変数に格納しているので、
順不同で、空欄スは0番の枚数(shiharai)、空欄セは2番の枚数(tsuri)になります。

6行目の空欄ソは判定条件で「最小値の計算では,これまでの払い方での最小枚数を変数min_maisuに記憶しておき,それより少ない枚数の払い方が出るたびに更新している」というのが対応しています。
つまり今までの最小が変数min_maisuに格納されているので、今回算出された枚数と比較する必要があります。
今回の算出結果は変数maisuに格納されているので、空欄ソは0番のmaisuになります。
空欄タは、最小枚数の更新処理と予想が付くので、1番のmin_maisuとなります。

はじめの1ループ目だけシミュレーションしていきます。
3行目で変数tsuriに0が代入されます。
4行目は46+0で変数shiharaiに46が代入されます。
5行目の枚数(46)は6、枚数(0)は0なので、変数maisuに合計値の6が代入されます。
6行目は6小なり100はTRUEになるので、min_maisuが6で更新されます。
今回の第3問の解説は以上になります。
最後までご視聴ありがとうございました。
