
No.002ファラデーの電磁誘導の法則
はじめに
ファラデーの電磁誘導の法則は学ぶ前からでもなんとなく聞いたことがある人が少なくはないのではないでしょうか?私が電磁誘導と聞いて1番最初に思い付くのが発電機とか電動機ですね。 今回はそんなファラデーの法則をまとめてみたいと思います。
物理的意味
「ある空間で磁束密度が時間変化したときにその変化を妨げる向きに渦巻く電場を生む」である。
微分形

引用
https://diracphysics.com/portfolio/electromagnetism/S0/eFaradaylaw.html
∇:微分演算子(ナブラ)
E:電場
B:磁束密度
∂/∂t:時間tに関する偏微分(係数)
式から分かるように電場と磁場の相互作用がこの法則によって約束される。
積分形

引用
長岡洋介、物理学入門コース新装版電磁気学11-変動する電磁場,岩波書店, 2024,p.226
t:閉曲線C上での各点における単位接線ベクト
ル
右辺のΦは1巻きあたりの磁束であり
閉ループや閉回路などに貫く磁束密度Bを面積
分したもので左辺にストークスの定理を適用す
れば微分形が導ける。今までの式にマイナスがついていたがこれはレンツの法則によって考慮された。
レンツの法則

引用
https://detail-infomation.com/lenzs-law/
渦なしの法則

引用
https://diracphysics.com/portfolio/electromagnetism/S1/enovortex.html

引用
https://diracphysics.com/portfolio/electromagnetism/S1/enovortex.html
この法則の意味として静電気力は保存力であることが挙げられる。電場Eはある電荷分布から単位電荷1[C]にかかるクーロン力であった。
積分形の式を見てもらうと分かるが今この積分形は始点と終点が一致する周回積分である。この積分値がゼロということは積分経路によらない量が同じ点で同じ値を持っていることを示唆している。(後の静電ポテンシャルφ)故にEは保存力であると言える。
ベクトルの回転

引用
https://diracphysics.com/portfolio/physicalmath/S3/protation.html#question2
rotV,culVとも表す。
解釈
回転とは単位面積あたりのベクトルの渦のことである。
ストークスの定理
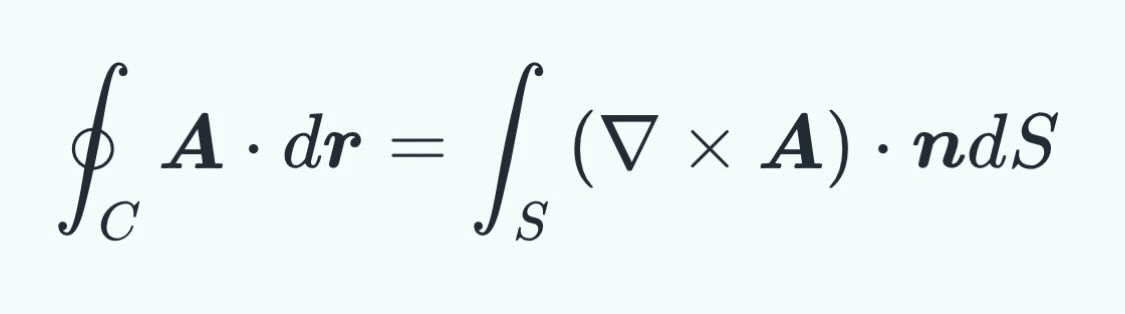
引用
https://manabitimes.jp/math/1900
数学のベクトル解析で学ぶ
終わりに
今回はマクスウェル方程式のファラデーの電磁誘導の法則についてまとめました。互い無関係とされていた電場と磁場を結びつけ、ローレンツ力関係で色々繋がってくるらしいから後日追加します!
