
第一回 これだけ!行列の四則演算 (線形代数)
まどろっこしい前置きは無しにしましょう。行列とその計算方法について、まずは計算の仕方を身につけましょう。
1.行列とは
行列は数字を矩形状に並べたもので、行と列から成ります。例えば、2行3列の行列は

です。m行n列の行列は以下のように表されます。

ここで、例えば2行目1列目の要素は$${a_{21}}$$などと書くのが一般的です。
2.行列の足し算
例えば、以下の2つの行列 A と B を考えます。

これらの行列を加算する場合、同じ位置にある要素同士を足し合わせます。つまり、

と計算できます。
3.行列の引き算
行列の引き算では足し算と同様に、同じ位置にある要素同士を引きます。例えば、以下の2つの行列 A と B を考えます。

これらの行列を引き算する場合、下のように同じ位置にある要素同士を引きます。

4.行列の掛け算
掛け算はちょっと複雑ですよ。
以下の2つの行列 A と B を掛け算することを考えます。
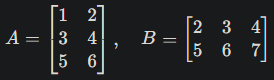
ここで、$${A\times B}$$を計算したいとき、次の手順を踏んで計算してください。
①答えの行数と列数を知ろう
実は、$${(\bold a行b列の行列)\times(b行\bold c列の行列)}$$の答えは$${\bold a行\bold c列の行列}$$になります。×の左側の行列の行数と右側の行列の列数を見ればいいわけですね。今回の$${A\times B}$$の場合、$${(3行2列の行列)\times(2行3列の行列)}$$なので、答え($${C}$$行列としよう)は下のような$${3行3列の行列}$$になるわけです。

②それぞれの行列に線を引こう
$${A\times B}$$の場合、$${×}$$の左側の行列($${A}$$)では行ごとに線を描き、$${×}$$の右側の行列($${B}$$)では列ごとに線を描いてください。下のようになるはずです。

③行列の各要素を掛け合わせていこう
例えば答えの行列$${C}$$の要素の一つ、$${c_{21}}$$を計算していきましょう。この要素は2行目の1列目なので、上で書いた赤い線の2行目と青い線の1列目の要素同士をかけ合わせます。つまり、、、
$${c_{21}=3・2+4・5=26}$$
これを後8回頑張って下のように計算します。

すると上のように答えが出るわけですね。
注意!
行列の順番が変わると、掛け算の結果も異なります。つまり、 $${A\times B}$$と $${A\times B}$$は大抵の場合は異なる結果になります。注意してください。例えば上の例だと、、、
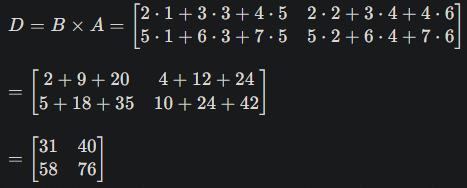
このようにそもそも答えの行数も列数も異なるわけです。上の①~③の手順通りに計算すれば間違いは起きないはずですが念のため。
割り算は?
割り算は一般的にはあまり計算されることがないように感じます。強いて言えば逆行列を掛ければ割り算と同じ結果が得られます。ここでは割愛します。
まとめ
ここでは行列とは何か、と行列の基本的な計算方法について解説しました。
私のブログで勉強するのは大変ありがたいですしうれしいですが、このブログは理工系として必要最低限の会話ができる知識をお伝えするのみなので、書籍と合わせて勉強することでより効率的にそしてさらに深く勉強が進むかと思います。まずこちらの書籍を手に取ってみて、並行して学んでみるのもいいかもしれません。
次回は行列の四則演算にまつわる法則について解説します。
次回はこちら↓
