
第10回 これだけ!線形空間と線形変換(線形代数)
前回は何を目的にこの講座を投稿しているのかについて解説しました。
今回は線形空間と線形変換の性質について解説していきます。
1.前置き。線形空間
線形変換についていきなり説明する前に、線形変換が行われる空間について説明します。
ベクトル$${\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}}$$について次のような式を考えましょう。
$$
\overrightarrow{x}=k\overrightarrow{a}+m\overrightarrow{b}+n\overrightarrow{c}
$$
k,m,nは任意の実数として、このようにベクトルの線形結合(ベクトルを定数倍したもの同士の足し合わせ)によって計算されるベクトル$${\overrightarrow{x}}$$がとりうる空間を線形空間(ベクトル空間)と呼びます。例として次のようなベクトルは私たちが普段見慣れた3次元の直交座標系の座標軸を表しますが、
$$
\overrightarrow{a}=
\begin{pmatrix}
1\\0\\0
\end{pmatrix}\quad
\overrightarrow{b}=
\begin{pmatrix}
0\\1\\0
\end{pmatrix}\quad
\overrightarrow{c}=
\begin{pmatrix}
0\\0\\1
\end{pmatrix}
$$
これにk,m,nを当てはめて計算したベクトル達の集合も線形空間です(すべての空間が表せますね)。私たちが解き明かしたい物理現象はこういった線形空間内で起こっています。したがって線形空間の判定法や線形空間ではない場合については特にここでは触れません。悪しからず。
2.線形独立と基底
ベクトル$${\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}}$$が線形独立であるとは、次の式において、
$$
k\overrightarrow{a}+m\overrightarrow{b}+n\overrightarrow{c}=0
$$
この式の解が、
$$
k=m=n=0
$$
以外に存在しないことを言います。つまりあるベクトルがほかのベクトル同士の線形結合で表せなければ線形独立となります。ちなみに表せてしまった場合はそのベクトルは線形従属と呼びます。
また下のベクトル達に登場してもらいましょう。
$$
\overrightarrow{a}=
\begin{pmatrix}
1\\0\\0
\end{pmatrix}\quad
\overrightarrow{b}=
\begin{pmatrix}
0\\1\\0
\end{pmatrix}\quad
\overrightarrow{c}=
\begin{pmatrix}
0\\0\\1
\end{pmatrix}
$$
このベクトル達はほかの二つのベクトルの線形結合によってあらわされるでしょうか?…どうあがいても無理ですね?なので、これら3つのベクトルは線形独立です。
またこれらのベクトルの線形結合によって空間全体を表現できるようなベクトルを基底と呼びます。つまり先ほどのベクトル達は基底ですし、何ならそれぞれ長さが1でお互いに直行する基底です。このような基底を標準基底と呼びます。
また覚えておくと良いのが線形独立であるかの判定です。ベクトル$${\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}}$$を行列$${A}$$として以下のようにくくった時、
$$
A=
\begin{pmatrix}
\overrightarrow{a}\quad\overrightarrow{b}\quad\overrightarrow{c}
\end{pmatrix}
$$
次の式が成り立てばベクトル$${\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}}$$が線形独立だと言えます。
$$
|A|\ne 0
$$
余談ですが、$${AX=0}$$のような同次方程式が$${X=0}$$のみを解としてを持つための条件は$${|A|\ne 0}$$となります。これも証明は省きますね。
3.基底が直交している場合に成り立つ性質
地味に重要です。予告しておくと数回先にこの性質が出てきます。
以下の互いに直交する基底$${\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}}$$について、
$$
\overrightarrow{a}=
\begin{pmatrix}
a_{1}\\a_{2}\\a_{3}
\end{pmatrix}\quad
\overrightarrow{b}=
\begin{pmatrix}
b_{1}\\b_{2}\\b_{3}
\end{pmatrix}\quad
\overrightarrow{c}=
\begin{pmatrix}
c_{1}\\c_{2}\\c_{3}
\end{pmatrix}
$$
以下のように行列$${U}$$としてくくった時に、
$$
U=
\begin{pmatrix}
\overrightarrow{a}\quad\overrightarrow{b}\quad\overrightarrow{c}
\end{pmatrix}
$$
以下の関係が成り立ちます。覚えておきましょう。
$$
U^TU=I
$$
これ、皆さんの力で証明してみましょうか。そんなに難しくありません。
ヒントは"内積"です。
4.線形変換のイメージをつかもう
本題です。次のような正方行列$${A}$$とベクトル$${\overrightarrow{r}}$$があるとき、
$$
A=
\begin{pmatrix}
a&b\\
c&d
\end{pmatrix}\quad
\overrightarrow{r}=
\begin{pmatrix}
x\\y
\end{pmatrix}
$$
この時、次のような行列$${A}$$とベクトル$${\overrightarrow{r}}$$の積を考えます。
$$
A\overrightarrow{r}=
\begin{pmatrix}
a&b\\
c&d
\end{pmatrix}
\begin{pmatrix}
x\\y
\end{pmatrix}
=
\begin{pmatrix}
ax+by\\
cx+dy
\end{pmatrix}
$$
このように行列とベクトルをかけ合わせることで新たなベクトル$${\overrightarrow{r^{'}}}$$が誕生します。
$$
\overrightarrow{r^{'}}=
\begin{pmatrix}
x^{'}\\y^{'}
\end{pmatrix}
=
\begin{pmatrix}
ax+by\\
cx+dy
\end{pmatrix}
$$
このように元のベクトルの成分を線形結合して新たなベクトルを生み出すとき、この変換を線形変換と呼びます。
ちょっとわかりずらいですか?では例として次の行列とベクトルを考えましょう。
$$
A=
\begin{pmatrix}
4&3\\
-3&4
\end{pmatrix}\quad
\overrightarrow{r}=
\begin{pmatrix}
1\\1
\end{pmatrix}
$$
まず考え方としては、行列Aは実は2つのベクトルの寄せ集めでできています。
$$
A=
\begin{pmatrix}
u_{1} u_{2}
\end{pmatrix}\quad
u_{1}=
\begin{pmatrix}
4\\-3
\end{pmatrix}\quad
u_{2}=
\begin{pmatrix}
3\\4
\end{pmatrix}
$$
これを画像で表すと次のようになります。

今、変換前の座標軸(標準基底)に対して、行列$${A}$$で定義される新たな座標軸(緑色)を考えるわけです。こう見ると新たな座標軸は元の標準基底を回転させてから拡大した、という見方ができますね。
ここでベクトル$${\overrightarrow{r}}$$を線形変換すると新たなベクトル$${\overrightarrow{r^{'}}}$$は次のような位置関係になります。紫のベクトルが変換前の$${\overrightarrow{r}}$$、赤のベクトルが変換後の$${\overrightarrow{r^{'}}}$$です。何かに気づきませんか?

そうですね。ベクトルも変換することで回転して、そして拡大しているのが分かります。しかも回転角、拡大率は座標軸のそれと同一です。
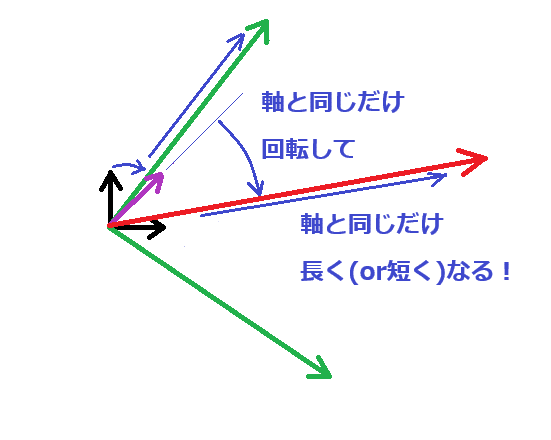
つまり線形変換とは、新たな基底を行列として定義したときに、変換前後で基底とベクトル同士の位置関係が変わらないような、新たなベクトルが作られるというわけですね。
少し具体的に言えば元の座標軸に光が差した時の影が新たな座標軸なら、元の座標軸上にあるベクトルの影こそが変換後のベクトルになるわけですね。伝わるかなこの表現……
5.不思議な線形変換
例題がてら、次のような線形変換を考えましょう。
$$
A=
\begin{pmatrix}
-2&4\\
3&-3
\end{pmatrix}\quad
\overrightarrow{r}=
\begin{pmatrix}
4\\3
\end{pmatrix}
$$
このベクトル$${\overrightarrow{r}}$$の$${A}$$による線形変換を求めてみましょう。……
不思議でしょう?基底を変えているのに変換前と変換後でベクトルが全く同じになるのです。このように線形変換してもベクトルの方向が不変なベクトルを$${A}$$の固有ベクトルといいます。次回はその固有ベクトルについて説明しましょう。
まとめ
今回は線形空間と線形変換について駆け足で解説しました。本来であれば2回に分けて説明すべき内容ですが、理解できたでしょうか?
このブログは理工系として必要最低限の会話ができる知識をお伝えしていますが、書籍と合わせて勉強することでより効率的にそしてさらに深く勉強が進むかと思います。まずこちらの書籍を手に取ってみて、並行して学んでみるのもいいかもしれません。
次回は固有ベクトルと固有値とは何か、そして固有方程式の解き方についてです。次はこちら↓
